【数据结构】串（二）—— 朴素模式匹配算法

前言

字符串模式匹配:在主串中找到与模式串相同的子串，并返回其所在位置。

在数据结构中，主要的字符串模式匹配算法有两种：朴素模式匹配算法和KMP算法。

朴素模式匹配算法

假设主串⻓度为n，模式串⻓度为 m

朴素模式匹配算法：将主串中所有⻓度为 m 的⼦串依次与模式串对⽐，直到找到⼀个完全匹配的⼦串，或所有的⼦串都不匹配为⽌。

1. 朴素模式匹配算法过程

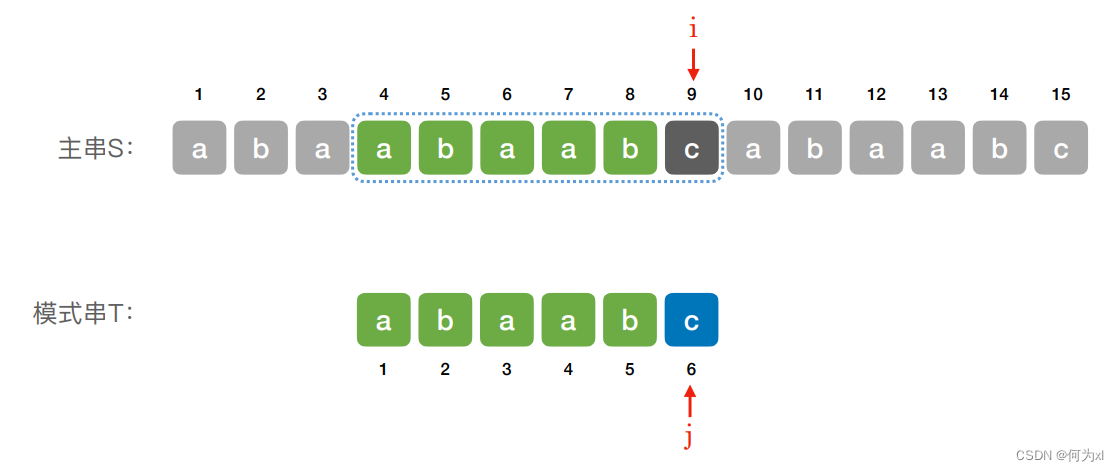
首先定义指针 i 与 j ，确认主串与模式串对应的位置下标。

匹配失败图解

若当前⼦串匹配失败，则主串指针 i 指向下⼀个⼦串的第⼀个位置，模式串指针 j 回到模式串的第⼀个位置

注：此时 i = i - j + 2 是指 i - j 表明在比较字符串最开始位置处的前一个位置，故需要加2. i - j 指示的位置如下图所示。

匹配成功图解

若 j > T.length，则当前⼦串匹配成功，返回当前⼦串第⼀个字符的位置 —— i - T.length

2. 算法代码

#define MAXLEN 255      //预定义最大串长为255
typedef struct {
    char ch[MAXLEN];    //每个分盘存储一个字符
    int length;         //串的实际长度
) SString;

int Index(SString S,SString T){
    int i=1,j=1;
    while( i<=s.length && j<= T.length){
        if(S.ch[i] == T.ch[j] ){
            ++i; ++j;//继续比较后继字符
        }
        else{
            i = i-j+2;
            j = 1;
        //指针后退重新开始匹配
        }
    }
    if(j>T.length)
        return i - T.length;
    else
        return 0;
}

3. 性能分析

设主串⻓度为 n，模式串⻓度为 m，（注：很多时候，n >> m）则：

• 匹配失败最坏的情况，每个⼦串都要对⽐ m 个字符，共 n-m+1 个⼦串，复杂度 = O((n-m+1)m) = O(nm)

• 匹配失败最好的情况，每个⼦串的第⼀个字符就匹配失败，共 n-m+1 个⼦串，复杂度 = O(n-m+1) = O(n)

• 匹配成功最好的情况，第一个⼦串的就匹配成功，复杂度 = O(m)

4. 要点

1. 主串共 n-m+1 个⼦串；
2. 主串指针匹配失败更新时i = i-j+2
3. 当 模式串指针 j >T.length时， 返回的位置为 i - T.length