机器学习基础整理(第四章) - 核方法 (Kernel Methods)

核方法

将给定的数据嵌入到一个空间中，在该空间中可以将模式发现为线性关系。
两个步骤:

• 映射 由 所谓的核函数 (kernel function) 隐式定义 (取决于有关数据源模式的领域知识 domain knowledge regarding pattern in data source)。
• 使用健壮的通用算法。

算法高效，且需要 在数据项的大小和数量上是多项式的 计算资源，嵌入空间 (embedding space) 的维度呈指数增长，不影响计算负担。

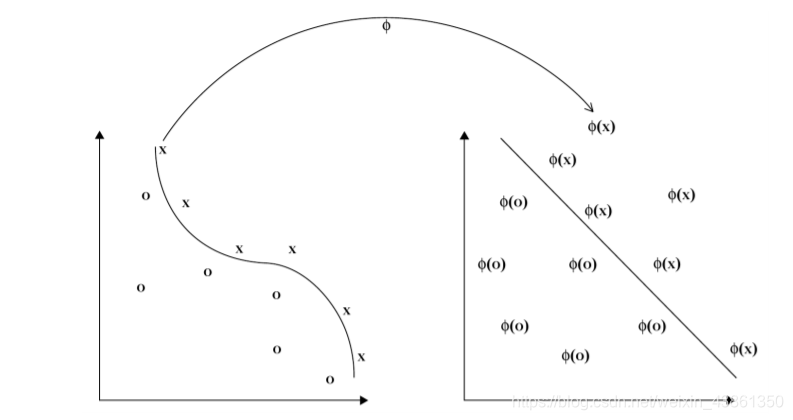
函数 $\varphi$ 将数据 嵌入到 特征空间中，非线性模式 现在以 线性模式 出现。

线性回归回顾

前面的推导过程详见另一篇文章
线性回归

最终，预测机的输出是权重和新的特征向量的内积
$$g(x)=<W,x>$$

对于可逆的 $X{X}^T$，我们能将 $W$ 写为:
$$W=(X{X}^T{)}^{-1}XY=X{X}^T(X{X}^T{)}^{-2}XY=X\alpha$$
$$W=\sum _{i=1}^m{x}_i{\alpha }_i$$
其是训练数据的线性组合。

解权重向量的两种表示：

• $W=(X{X}^T{)}^{-1}XY$ 原始形式 (primal form)
• $W=X\alpha$ 对偶形式 (dual form)

若 $X{X}^T$是非可逆的，我们可能通过要求权重的 二范数 (2-norm) 很小， 使用 伪逆 (pseudo-inverse) 或 正则化 (regularize) 初始问题 ，如 最小化 $||W|{|}^2$

岭回归回顾

前面的推导过程详见另一篇文章
岭回归

其中
$$W=(X{X}^T+\lambda I{)}^{-1}XY$$
可以被类似于普通回归的做法，写为:
$$W=X\alpha$$
其中 $\alpha$ 是:
$$(G+\lambda I{)}^{-1}Y$$
而 $G=X^{T}X$被称为 格拉姆矩阵 (Gram matrix)。每一个 $G$ 的元素都是一个内积，$<x_i,x_j>$，使得:
$$G_{i,j}=<x_i,x_j>$$

格拉姆矩阵的解释

其预测函数是:

与普通回归一样，我们有两种形式的岭回归解:

• $W=(X{X}^T+\lambda I{)}^{-1}XY$ 原始形式 (primal form)
• $W=X\alpha$ 对偶形式 (dual form)

原始形式显式计算，而 对偶形式 表示为训练样本的线性组合。

在原始形式中，我们求解 $(N\times N)$ 方程组，而在 对偶形式 中，我们求解 $(m\times m)$ 系统。

若 特征维度 $N\gg m$ (样本数)，计算优势就很明显了。

关键观察：岭回归算法 可以 以只需要样本点之间的内积的形式 求解。

内核定义的非线性映射 (Kernel-defined nonlinear mapping)

线性回归中的假设是特征 (自变量) 和预测结果变量 (因变量) 之间的关系是线性的，那如果不是呢？

好的策略是将特征映射到允许关系为线性的新特征空间，然后应用岭回归。

类似地，我们可以对用于分类的线性判别式 (linear discriminant) 做同样的事情

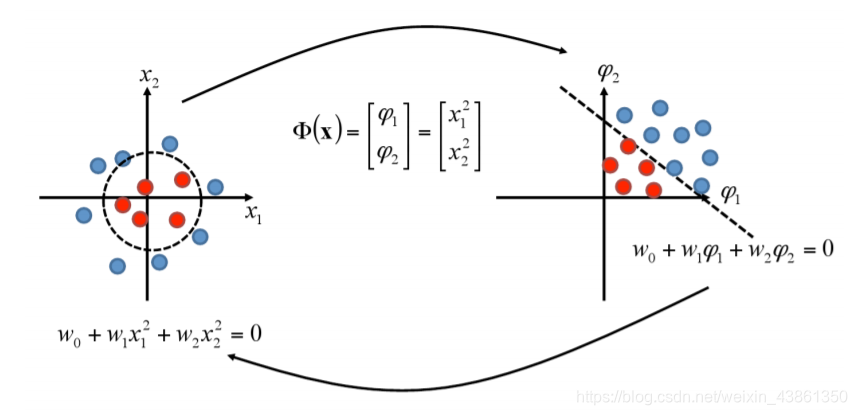
考虑一个嵌入映射:

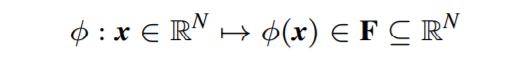
选择映射 $\varphi$ 使其旨在将非线性关系转换为线性关系。

映射 $\varphi$ 将给定的数据集 $S$ 重新编码为 { ( ϕ ( x i ) , y i ) , . . . , ( ϕ ( x m ) , y m ) } \{(\phi(x_i), y_i), ..., (\phi(x_m), y_m)\} {(ϕ(xi​),yi​),...,(ϕ(xm​),ym​)}，这代表了数据集中的 $M$ 个样本。

回想一下，岭回归解的有效 对偶形式(dual form) 需要由内积组成的 Gram 矩阵。
$$G_{i,j}=<\varphi (x_i),\varphi (x_j)>$$

$\alpha$ 的计算复杂度 为 $O(m^3+m^{2}N)$ 以及 让预测机估算一个新样本的复杂度为 $O(mN)$

事实证明，内积可以直接在输入空间中计算，而不是首先使用核函数计算 $\phi (x)$。

定义: 一个核 是一个函数，$k$，其对于所有 $x,z\in S$ 满足:
$$k(x,z)=<\varphi (x),\varphi (z)>$$
其中 $\varphi$ 是从 $S$ 到 一个内积特征空间 $F$ 的映射。

例子

考虑一个二维输入空间 $x\subseteq {\mathbb{R}}^2$ 以及 特征映射:

$F$ 中的线性函数假设就以以下形式存在:

因此，$k(x,z)=<x,z{>}^2$ 是一个核函数，$F$ 是对应的特征空间。

另一个例子

考虑一个二维输入空间 $x\subseteq {\mathbb{R}}^2$ 以及 特征映射:

同一个内核 计算 这个特征空间的内积。
因此特征空间 不是由 核函数 唯一确定的。

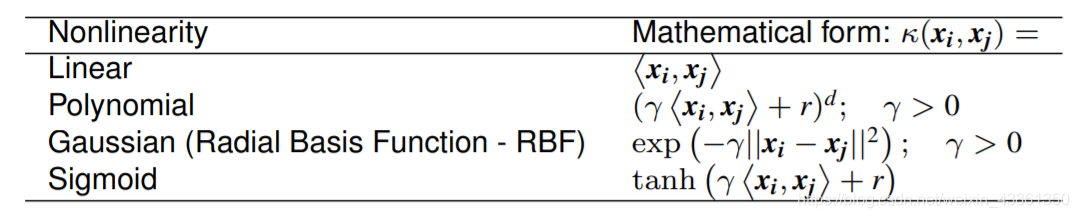
下图展现了常用的核函数 ($\gamma ,r,d$ 都是参数)

另一个例子:
使 $x=[146{]}^T$ 以及 $z=[352{]}^T$ 作为我们需要通过映射函数 $\varphi (.)$ 映射到一些特征空间 $F$ 的两个特征向量。让我们考虑使用 和 RBF 特征空间有关的参数为$\gamma =0.2222$ 的核函数。两个向量的内积的值为 $<\varphi (x),\varphi (z)>$，我们需要计算 $k(x,z)=exp(-\gamma ||x-z|{|}^2)$

岭回归的核

回到岭回归的公式中，我们能发现出现在岭回归解中的 Gram 矩阵的每一项都是输入空间中数据的内积。
映射 $\phi (\cdot )$ 到高维特征空间 $F$，意味着可以使用特征空间的适当内核计算 Gram 矩阵的每个条目。

$$G_{i,j}=<\varphi (x_i),\varphi (x_j)>=k(x_i,x_j)$$

核化 (kernalization) 提供了一种处理问题中可能存在的非线性关系的方法（例如回归、分类、降维等）

支持向量机 (Support Vector Machine)

考虑一个有数据 $x_i(i=1,...,m)$ 并拥有 对应标签 $y_i=\pm 1$ 的二分类任务，其决策函数为:
$$g(x)=sign(<w,x>+b)$$

对于可分离的数据集，若 $\forall i,y_i(<w,x>+b)>0$， 所有数据都将被正确分类。

定义规范超平面 (canonical hyperplane)，使得 $<w,x>+b=1$ 表示分离平面一侧的最近点，而 $<w,x>+b=-1$ 表示另外一侧的最近点。

上图是 SVM 的分离平面

分离平面 (seperating plane): $<w,x>+b=0$ 以及 法向量 $\frac{w}{||w||}$

边距 (margin) 由 $x_1-x_2$ 在分离平面上的投影给出。

$<w,x_1>+b=1$ 以及 $<w,x_2>+b=-1$， 边距为 $\gamma =1/||w||$

我们通过最小化
$$min[\frac{1}{2}||w|{|}^2]$$
其中 $\forall i,y_i(<w,x>+b)\ge 1$

能最大化边距 $\gamma =1/||w||$

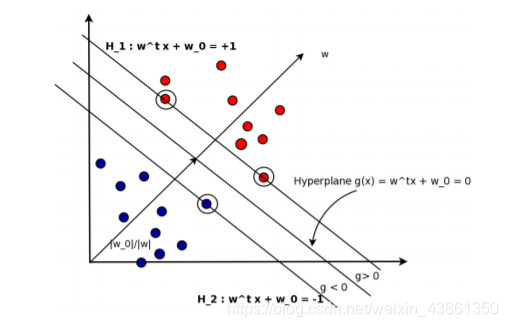
上图是 SVM 分离平面的细节

学习任务简化为最小化 原始目标函数 (primal objective function)：
$$L=\frac{1}{2}(<w,w>)-\sum _{i=1}^m{\alpha }_i(y_i(<w,x_i>+b)-1)$$
其中 ${\alpha }_i$ 是拉格朗日乘数 (Lagrange multipliers) 以及 ${\alpha }_i\ge 0$

在对 $b$ 和 $w$ 取导数并适当代入上式之后，我们能得到 对偶目标函数 (dual objective function)。
$$W(\alpha )=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j<x_i,x_j>$$
该式要相对于受下述条件约束的 ${\alpha }_i$ 最大化:
$${\alpha }_i\ge 0,\sum _{i=1}^m{\alpha }_i{y}_i=0$$

由上式表示的二次程序 (quadratic program) 给出了具有最大边距 (maximal margin) 的可分离数据的最佳分离超平面 (optimal seperating hyperplane)。

上式指示了我们可以在不可分数据 (inseparable data) 的情况下，通过应用 映射 $\varphi (.)$，可以将 计算内积 的内核合并到特征空间中。

映射通过下述实现:

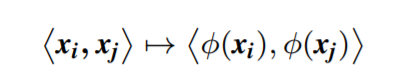
请注意，我们不需要知道 $\phi (x_i)$ 的函数形式，因为内核的选择隐含地定义了它:
$$k(x_i,x_j)=<\varphi (x_i),\varphi (x_j)>$$

因此，之前的SVM对偶目标函数的内核版本就是:

$$W(\alpha )=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_{j}k(x_i,x_j)$$
该式要相对于受下述条件约束的 ${\alpha }_i$ 最大化:
$${\alpha }_i\ge 0,\sum _{i=1}^m{\alpha }_i{y}_i=0$$

比如，内核可以被选择为 $k(x_i,x_j)=exp(-\gamma ||x_i-x_j|{|}^2)$

对于新的测试数据 $z$，决策函数变成:
$$f(z)=sign(\sum _{i=1}^m{y}_i{\alpha }_{i}k(x_i,z)+b)$$

软边距 (Soft Margin)

噪点 (noisy) 和离群值 (outliers) 会导致 模型 不好的泛化能力。
SVM 通过 引入 软边距 来减少它们的影响。

$$W(\alpha )=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_{j}k(x_i,x_j)$$
该式要相对于受下述条件约束的 ${\alpha }_i$ 最大化:
$${\alpha }_i\ge 0,\sum _{i=1}^m{\alpha }_i{y}_i=0$$

两种计算噪点和离群值的方式:

• 使用 $L_1$ 范数误差 并 在上式引入 框约束(box constrain) $0\le {\alpha }_i\le C$
• 使用 $L_2$ 范数误差 并在 上式 核矩阵 $k(x_i,x_j)$ 的 前导对角线 (leading diagonal) 上添加一个小的正 常量(small positive constant) 使其变成 $k(x_i,x_j)+\lambda$

通过选择 参数 $C$ 和 $\lambda$ 来权衡训练 误差和泛化能力，我们可以使用验证集实现这一点。

关键

通过考虑基于内核的公式 (kernel-based formulation)，可以使所有线性模型处理非线性。

可以在输入空间中 执行特征空间中的内积 的内核技巧 (kernel trick) 使得处理高维 成为可能。

由于 内核技巧 (kernel trick)，结果证明我们不需要知道映射 $\varphi (.)$ 的形式，只要我们知道对应于特征空间的核函数 $k(.,.)$。

有许多内核可被用于内核化，内核也可以从数据中被学习。也可以在同一个公式中使用多个内核。

降维方法 (Dimensionality Reduction)

数据可能具有大量特征，通常需要降低其维度，或找到保留其某些属性的低维表示 (lower-dimensional representation)。

为什么需要降维 (或流形学习 manifold learning):

• 计算 (computational): 压缩初始数据作为预处理以加快后续操作。
• 可视化 (visualization): 通过将原始数据映射到二维或三维空间，将数据可视化以进行探索性分析 (exploratory analysis)，这使得可视化更容易。
• 特征提取 (feature extraction): 生成更小的，更有效或有用的特征集。

主成分分析 (Principle Component Analysis - PCA)

在之前，我们了解了 可以通过一种 Ridge 正则化方式 (ridge regularization) 对特征进行加权，或我们可以通过 Lasso 正则化方式 (lasso regularization) 来选择重要特征。

假设我们想要减少用于表示被建模对象的特征数量，或者，假设我们想要找到一种保留原始数据某种属性的低维表示。

在主成分分析 (PCA) 的公式中，我们可以从中发现 最大化数据方差 (maximize the variance of the data) 的新维度。

上图表示 主成分的几何。

为什么我们需要最大化方差？

信噪比 (signal-to-noise ratio SNR) 衡量 信号强度 相对于 噪声强度 的大小。
$$SNR=\frac{{\sigma }_s^2}{{\sigma }_N^2}$$
因此最大化信号的方差是有意义的，协方差用于两个或多个特征。

如果上图中所示的二维数据层中 (即去除了平均值)，我们在二维中 拟合高斯 (Gaussian)，沿 $PC1$ 轴的高斯将具有更大的方差。因此，选择使方差最大化的轴是有意义的。

考虑 $m$ 个数据样本 S = { x 1 , . . . , x m } S=\{x_1, ..., x_m\} S={x1​,...,xm​}，一个特征映射 $\Phi :X\to {\mathbb{R}}^N$

数据矩阵 $X\in {\mathbb{R}}^{N\times m}$，以及定义 { Φ ( x 1 ) , . . . , Φ ( x m ) } \{\Phi(x_1), ..., \Phi(x_m)\} {Φ(x1​),...,Φ(xm​)}

第 $i$ 个数据被表示为 $x_i=\Phi (x_i)$，也就是 $X$ 矩阵 的第 $i$ 列，这是一个 $N$ 维向量。

降维技巧旨在找到 $k\ll N$，即数据的 $k$ 维表示，$Y\in {\mathbb{R}}^{k\times m}$，其在某种程度忠于原始表示 $X$。

让 $k\in [1,N]$，$X$ 作为一个 以均值为中心 (mean-centred) 的矩阵。

使 $P_k$ 是一组 $k$ 维 k秩正交投影矩阵 (rank-k orthogonal projection matrices)

投影矩阵 与 线性向量空间 ${\mathbb{R}}^N$ 的子空间 ${\mathbb{R}}^{k<N}$ 相关联，并且具有以下属性，它们是唯一的方阵，可将向量空间中的任何向量 $x$ 投影到子空间中。

PCA 包括将 $N$ 维数据投影到 $k$ 维线性子空间中，以最小化重构误差，重构误差是原始数据和投影数据之间 $L_2$ 距离的平方。

问题就变成了:

对于上式的优化问题，可以证明若 $P^{\ast }$ 是最优正交投影矩阵，则其形式为 $P^{\ast }=u_k{u}_k^T$

$U_k\in {\mathbb{R}}^{N\times k}$ 是 由 前 k 个奇异向量 $C=\frac{1}{m}X{X}^T$ 组成的矩阵，样本协方差和 $X$ 相关。

$X$ 的 $k$ 维表示 从 $Y=U^{T}X$ 得来。

通过协方差的定义，$C$ 的 顶部奇异向量 (top singular vectors) 是数据中方差最大的方向。

其相关的奇异值等于方差。

PCA 投影到最大方差的子空间。

请注意 (无需证明) 对于任意 实矩阵 $A\in R^{m\times n}$，其奇异值分解 (SVD) 是这样的，存在:

核主成分分析 (Kernel Principle Component Analysis)

之前考虑的映射 $\Phi (.)$ 将被映射到任意 复现内核 (reproducing kernel) 希尔伯特空间 (Hilbert space $(RKHS{)}^2$) 的特征替换，我们只需要使用 于希尔伯特空间 对应的核函数 $k$ 。

我们需要展示 协方差矩阵 $C=\frac{1}{m}X{X}^T$ 的 SVD 分解 以及 核矩阵 $K=X^{T}X$ 之间的关系。

复现内核希尔伯特空间
使得 $K:X\times X\to R$ 作为 正定对称 (positive definite symmetric - PDS) 核。存在一个 希尔伯特空间 $H$ 以及 一个能将 $X$ 转为 $H$ 的 映射 $\Phi$，使得:
$$\forall x,x^{{}^{\prime }}\in X,K(x,x^{{}^{\prime }})=<\Phi (x),\Phi (x^{{}^{\prime }})>$$
此外，$H$ 还拥有以下属性，这被称为复现属性 (producing property)。
$$\forall h\in H,and\forall x\in X,h(x)=<h,K(x,.)>$$

$H$ 被称为 和 $K$ 关联 的 复现内核希尔伯特空间 (RKHS)。