Bezier 曲线 2D

Bezier 曲线于 1962 年由法国雪铁龙汽车公司的工程师 Bezier 所发表，主要应用于汽车的外形设计。虽然 Bezier 曲线早在 1959 年便由法国雷诺汽车公司的 De Casteljau 运用递推算法开发成功，但是 Bezier 却给出了曲线的详细的曲线计算公式。所以，命名为 Bezier 曲线.
Bezier 曲线由控制多边形唯一定义。
控制多边形的第一个顶点和最后一个顶点位于曲线上，多边形的第一条边和最后一条边表示了曲线在起点和终点的切矢量方向，其顶点则用于定义曲线的导数，阶次和形状。曲线的形状趋近于控制多边形并位于多边形所构成的土包内，改变控制多边形的顶点位置就会改变曲线的形状。
Bezier 曲线的直观交互性使得对设计对象的逼近达到了直接的集合化程度，使得起来非常方便。

Bezier 曲线的定义

给定 $n+1$ 个控制点 $P_i(i=0,1,2,\cdots n)$,则 $n$次Bezier 曲线的定义为
$P(t)={\sum }_{i=0}n{P}_i{B}_{i,n}(t),t\in [0,1]$
$P_i(i=0,1,2,\cdots ,n)$ 是控制多边形的 $n+1$ 个控制点. $B_{i,n}(t)$是 Bernstein 基函数，其表达式为

$$\begin{array}{c}{B}_{i,n}(t)=\frac{n!}{i!(n-i)!}{t}^i(1-t{)}^{n-i}=C_n^i{t}^i(1-t{)}^{n-i},i=0,1,2,\cdots n\end{array}$$

Bezier 函数是控制点关于 Bernstein 基函数的加权和，Bezier 曲线的次数为 n , 需要 n+1 个顶点来定义。
在工程项目中，最常见的是三次Bezier 曲线，其次数是二次Bezier 曲线，高次Bezier 曲线一般很少用

一次 Bezier 曲线, 当 n=1 时，Bezier 曲线的控制多边形有两个控制点 $P_0$ 和 $P_1$, Bezier 曲线是一次多项式，称为一次 Bezier 曲线，

$$P(t)=\sum _{i=0}^1{P}_i{B}_{i,1}(t)=(1-t)P_0+t{P}_1$$

二次 Bezier 曲线，当 n=2 时，Bezier 曲线的控制多边形有 3 个控制点， KaTeX parse error: Expected group after '_' at position 2: P_̲$ 、$P_1$和 $P_2$， Bezier 曲线是二次多项式，称为二次 Bezier 曲线，

$$P(t)=\sum _{i=0}^2{P}_i{B}_{i,2}(t)=(1-t{)}^2{P}_0+2t(1-t)P_1+t^2{P}_2$$
三次 Bezier 曲线，当 n=3 时，Bezier 曲线控制多边形有 4 个控制点， $P_0$ 、$P_1$、 $P_2$ 和 $P_3$， Bezier 曲线是三次多项式，称为三次 Bezier 曲线

$$P(t)=\sum _{i=0}^3{P}_i{B}_{i,3}(t)=(1-t{)}^3{P}_0+3t(1-t{)}^2{P}_1+3t^2(1-t)P_2+t^3{P}_3=(-t^3+3t^2-3t+1)P_0+（3t^3-6t^2+3t）P_1+(-3t^3+3t^2)P_2+t^3{P}_3$$

写成矩阵的形式为

$$P(t)=\left[\begin{array}{cccc}{t}^3& t^2& t& 1\end{array}\right]\left[\begin{array}{cccc}-1& 3& -3& 1\\ 3& -6& 3& 0\\ -3& 3& 0& 0\\ 1& 0& 0& 0\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\end{array}\right]$$

$$\begin{gathered} B_{0,3}(t)=(1-t{)}^3 \\ {B}_{1,3}(t)=3t(1-t{)}^2 \\ {B}_{2,3}(t)=3t^2(1-t) \\ {B}_{3,3}(t)=t^3 \end{gathered}$$

下面给出 QT + OPENGL 的二次的代码

#include <QtWidgets>
#include <QOpenGLWidget>
#include <QOpenGLFunctions>

class BezierCurveWidget : public QOpenGLWidget, protected QOpenGLFunctions {
public:
    BezierCurveWidget(QWidget* parent = nullptr)
        : QOpenGLWidget(parent) {}

protected:
    void initializeGL() override {
        initializeOpenGLFunctions();
        glClearColor(1.0f, 1.0f, 1.0f, 1.0f);
    }

    void resizeGL(int w, int h) override {
        glViewport(0, 0, w, h);
        glMatrixMode(GL_PROJECTION);
        glLoadIdentity();
        glOrtho(0, w, h, 0, -1, 1);
        glMatrixMode(GL_MODELVIEW);
    }

    void paintGL() override {
        glClear(GL_COLOR_BUFFER_BIT);

        // 控制点坐标
        QPoint p0(100, 300);
        QPoint p1(300, 100);
        QPoint p2(500, 300);

        // 设置线的颜色
        glColor3f(0.0f, 0.0f, 1.0f); // Blue color for lines

        // 绘制Bezier曲线
        glBegin(GL_LINE_STRIP);
        for (float t = 0.0f; t <= 1.0f; t += 0.01f) {
            QPoint p = calculateBezierPoint(t, p0, p1, p2);
            glVertex2i(p.x(), p.y());
        }
        glEnd();

        // 绘制控制点
        glPointSize(5.0f);
        glColor3f(1.0f, 0.0f, 0.0f);
        glBegin(GL_POINTS);
        glVertex2i(p0.x(), p0.y());
        glVertex2i(p1.x(), p1.y());
        glVertex2i(p2.x(), p2.y());
        glEnd();

        // 绘制连接线
        glBegin(GL_LINES);
        glVertex2i(p0.x(), p0.y());
        glVertex2i(p1.x(), p1.y());
        glVertex2i(p1.x(), p1.y());
        glVertex2i(p2.x(), p2.y());
        glEnd();
    }

    QPoint calculateBezierPoint(float t, const QPoint& p0, const QPoint& p1, const QPoint& p2) {
        float u = 1 - t;
        float tt = t * t;
        float uu = u * u;

        float x = uu * p0.x() + 2 * u * t * p1.x() + tt * p2.x();
        float y = uu * p0.y() + 2 * u * t * p1.y() + tt * p2.y();

        return QPoint(x, y);
    }
};

int main(int argc, char *argv[]) {
    QApplication a(argc, argv);

    QMainWindow window;
    BezierCurveWidget* bezierWidget = new BezierCurveWidget(&window);

    window.setCentralWidget(bezierWidget);
    window.resize(600, 400);
    window.show();

    return a.exec();
}

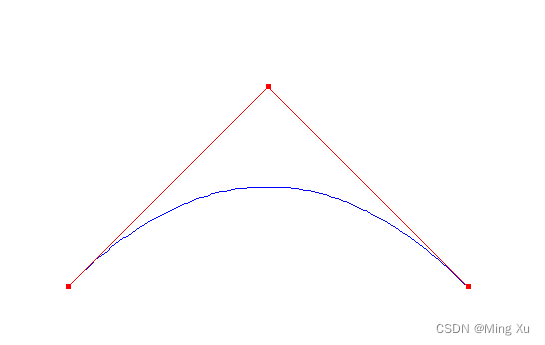
这里只需要替换一次和三次的计算部分即可。