凸包(Convex Hull)是包含给定点集合的最小凸多边形。凸包算法有多种实现方法,其中包括基于递增极角排序、Graham扫描、Jarvis步进法等。下面,我将提供一个简单的凸包算法实现,基于Graham扫描算法。
Graham扫描算法是一种用于求解平面点集的凸包问题的常见算法。凸包是包含给定点集合的最小凸多边形。Graham扫描算法的基本思想是通过选择一个特殊的起点,将点集按照极角排序,然后通过栈的操作来逐步构建凸包。
以下是Graham扫描算法的基本步骤:
-
选择极点: 从给定的点集中选择一个极点作为起始点。通常选择最下面且最左边的点,以确保算法的稳定性。
-
极角排序: 将其他所有点按照相对于极点的极角进行排序。极角可以使用反正切函数(atan2)计算。排序后的点集顺序将确定扫描过程中点的访问顺序。
-
扫描过程: 从第三个点开始,按照排序后的顺序逐个处理每个点。对于每个点,检查它与栈顶两个点的转向关系(顺时针、逆时针或平行)。如果是逆时针,将该点压入栈;如果是顺时针或平行,则出栈,直到找到逆时针为止。这确保了最终栈中的点构成凸包。
-
构建凸包: 扫描完成后,栈中的点就是凸包的顶点,它们按照逆时针方向排列。
Graham扫描算法的时间复杂度主要取决于对点的排序操作,通常为 O ( n log n ) O(n\log n) O(nlogn),其中n是点的数量。该算法的优势在于其相对简单的实现和较好的性能。然而,需要注意的是,在特定情况下,例如存在大量共线点的情况下,算法的性能可能会有所下降。
import matplotlib.pyplot as plt
import math
# 定义二维点的类
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
# 计算极角
def polar_angle(p0, p):
dx = p.x - p0.x
dy = p.y - p0.y
return math.atan2(dy, dx)
# 判断三个点的转向关系
def orientation(p, q, r):
val = (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y)
if val == 0:
return 0 # 平行
return 1 if val > 0 else 2 # 顺时针或逆时针
# Graham扫描算法
def convex_hull(points):
n = len(points)
if n < 3:
print("Convex Hull requires at least 3 points.")
return []
# 寻找最下面且最左边的点作为极点
pivot = min(range(n), key=lambda i: (points[i].y, points[i].x))
points[0], points[pivot] = points[pivot], points[0]
# 根据极角对其余点进行排序
points[1:] = sorted(points[1:], key=lambda p: (polar_angle(points[0], p), p.x, p.y))
# 构建凸包
hull = [points[0], points[1]]
for i in range(2, n):
while len(hull) > 1 and orientation(hull[-2], hull[-1], points[i]) != 2:
hull.pop()
hull.append(points[i])
return hull
# 示例点集
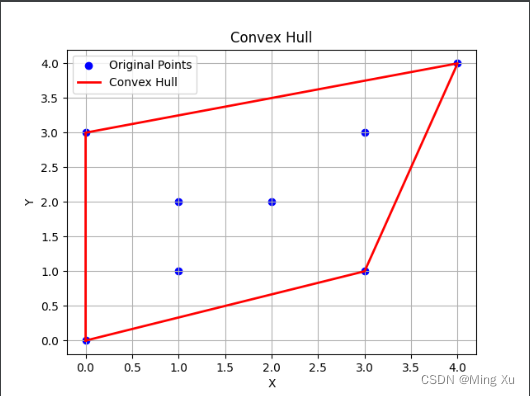
points = [Point(0, 3), Point(1, 1), Point(2, 2), Point(4, 4), Point(0, 0), Point(1, 2), Point(3, 1), Point(3, 3)]
# 计算凸包
convex_hull_points = convex_hull(points)
# 绘制原始离散点
x_values = [point.x for point in points]
y_values = [point.y for point in points]
plt.scatter(x_values, y_values, color='blue', label='Original Points')
# 绘制凸包
hull_x = [point.x for point in convex_hull_points]
hull_y = [point.y for point in convex_hull_points]
hull_x.append(convex_hull_points[0].x) # 闭合凸包
hull_y.append(convex_hull_points[0].y)
plt.plot(hull_x, hull_y, color='red', linestyle='-', linewidth=2, label='Convex Hull')
# 显示图例和图形
plt.legend()
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Convex Hull')
plt.grid(True)
plt.show()
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
// 定义二维点的结构体
struct Point {
double x, y;
// 构造函数
Point(double _x, double _y) : x(_x), y(_y) {}
// 用于排序的比较函数
static bool compare(const Point& a, const Point& b) {
return (a.y < b.y) || (a.y == b.y && a.x < b.x);
}
};
// 计算极角
double polarAngle(const Point& p0, const Point& p) {
double dx = p.x - p0.x;
double dy = p.y - p0.y;
return atan2(dy, dx);
}
// 判断三个点的转向关系
int orientation(const Point& p, const Point& q, const Point& r) {
double val = (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y);
if (val == 0) return 0; // 平行
return (val > 0) ? 1 : 2; // 顺时针或逆时针
}
// Graham扫描算法
std::vector<Point> convexHull(std::vector<Point>& points) {
size_t n = points.size();
if (n < 3) {
std::cerr << "Convex Hull requires at least 3 points." << std::endl;
return std::vector<Point>();
}
// 寻找最下面且最左边的点作为极点
size_t pivot = 0;
for (size_t i = 1; i < n; i++) {
if (points[i].y < points[pivot].y || (points[i].y == points[pivot].y && points[i].x < points[pivot].x)) {
pivot = i;
}
}
// 将极点移到数组的第一个位置
std::swap(points[0], points[pivot]);
// 根据极角对其余点进行排序
std::sort(points.begin() + 1, points.end(), [&points](const Point& a, const Point& b) {
double angleA = polarAngle(points[0], a);
double angleB = polarAngle(points[0], b);
return (angleA < angleB) || (angleA == angleB && (a.x < b.x || (a.x == b.x && a.y < b.y)));
});
// 构建凸包
std::vector<Point> hull;
hull.push_back(points[0]);
hull.push_back(points[1]);
for (size_t i = 2; i < n; i++) {
while (hull.size() > 1 && orientation(hull[hull.size() - 2], hull[hull.size() - 1], points[i]) != 2) {
hull.pop_back();
}
hull.push_back(points[i]);
}
return hull;
}
int main() {
// 示例点集
std::vector<Point> points = { {0, 3}, {1, 1}, {2, 2}, {4, 4}, {0, 0}, {1, 2}, {3, 1}, {3, 3} };
// 计算凸包
std::vector<Point> convexHullPoints = convexHull(points);
// 输出凸包的点
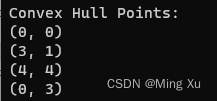
std::cout << "Convex Hull Points:" << std::endl;
for (const auto& point : convexHullPoints) {
std::cout << "(" << point.x << ", " << point.y << ")" << std::endl;
}
return 0;
}








 本文介绍了Graham扫描算法,一种用于求解平面点集凸包问题的方法。算法通过选择极点、极角排序和堆栈操作构建最小凸多边形,适用于求解给定点集的凸包。尽管时间复杂度为O(nlogn),但在大多数情况下表现出良好的性能。
本文介绍了Graham扫描算法,一种用于求解平面点集凸包问题的方法。算法通过选择极点、极角排序和堆栈操作构建最小凸多边形,适用于求解给定点集的凸包。尽管时间复杂度为O(nlogn),但在大多数情况下表现出良好的性能。














 373
373











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








