kmeans聚类
一、作业内容
在本练习中,您将实现K-means聚类算法并应用它来压缩图像。
数据集下载位置(包含吴恩达机器学课后作业全部数据集):data
二、作业分析
1、无监督学习:根据类别未知(没有被标记)的训练样本解决模式识别中的各种问题,称之为无监督学习,“监督”的意思可以直观理解为“是否有标注的数据”。
无监督学习的特点是,传递给算法的数据在内部结构中非常丰富,而用于训练的目标和奖励非常稀少。无监督学习算法学到的大部分内容必须包括理解数据本身,而不是将这种理解应用于特定任务。
无监督学习方法是在数据集中寻找规律性。这种规律性并不一定要达到划分数据集的目的,也就是说不一定要“分类”。比如,一组颜色各异的积木,它可以按形状为维度来分类,也可以按颜色为维度来分类 。
2、聚类是无监督学习的常见任务,就是将观察值聚成一个一个的组,每一个组都含有一个或者几个特征,聚类的目的在于把相似的东西聚在一起,而我们并不关心这一类是什么。 因此,一个聚类算法通常只需要知道如何计算相似度就可以开始工作了。例如无监督学习应该能在不给任何额外提示的情况下,仅依据一定数量的“狗”的图片特征,将“狗”的图片从大量的各种各样的图片中将区分出来。
k_means:无监督分类算法,不需要标签集
训练步骤:
首先KMeans算法需要有两个输入:
(1) K(聚类的个数)
(2) 训练集{
x
1
x_1
x1、
x
2
x_2
x2、…、
x
m
x_m
xm}
其中我们约定
x
i
x_i
xi∈
R
n
R_n
Rn(注意这里不需要加入
x
0
x_0
x0=1)
然后我们要随机初始化K个聚类中心 u 1 u_1 u1, u 2 u_2 u2,…, u K u_K uK,其中这些聚类中心都是n维的向量
第一个for循环代表遍历每一个样本,为每一个样本选择一个簇,也就是选择1~K个聚类中心的一个。其中选择的方法就是选择距离当前样本最近的聚类中心,也就是使得 m i n ∣ ∣ min|| min∣∣x_i − - −u_k ∣ ∣ 2 ||^2 ∣∣2
第二个for循环代表重新计算聚类中心, u k u_k uk代表聚类中心。假设样本1、5、6、9在第一个for循环中被划分到第二个簇,那么 c 1 c_1 c1= c 5 c_5 c5= c 6 c_6 c6= c 9 c_9 c9=2。并且 u 2 u_2 u2=[ x 1 x_1 x1+ x 5 x_5 x5+ x 6 x_6 x6+ x 9 x_9 x9]/4, u 2 u_2 u2是一个n维向量。
注意:
计算每个样本点到每类聚类中心点的距离(损失函数):
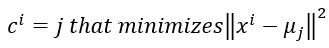
计算新的聚类中心点:
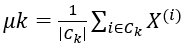
C
(
i
)
C^{{(i)}}
C(i) :
x
(
i
)
x^{(i)}
x(i)被划分到的簇的序号
μ
k
\mu _{k}
μk :第K个聚类中心
μ
C
i
\mu _{C^{i}}
μCi :表示
x
(
i
)
x^{(i)}
x(i)所属簇的聚类中心
3、随机初始化
下面推荐一个比较常见的初始化方法:
(1) 首先要保证簇数K<m(样本数)
(2) 随即从训练样本中选择K个样本作为初始的聚类中心
4、K-Means聚类算法有可能会出现局部最优的情况
处理方法:
尝试多次(100次)初始化k-means算法并实现,选择代价函数最小的作为最优解。一般对于聚类中心在2-10比较有效。
5、K值的选择
在进行K值选择的时候,可以尝试一下肘部法则
绘制K-代价曲线图
选择那个“拐点”作为我们K值的选择
如果曲线一直基本平缓,则只能根据实际的需要去选择K值
三、代码实战
我们将实施和应用K-means到一个简单的二维数据集,以获得一些直观的工作原理。 K-means是一个迭代的,无监督的聚类算法,将类似的实例组合成簇。 该算法通过猜测每个簇的初始聚类中心开始,然后重复将实例分配给最近的簇,并重新计算该簇的聚类中心。 我们要实现的第一部分是找到数据中每个实例最接近的聚类中心的函数。
引入所需函数库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
from IPython.display import Image
from skimage import io
from sklearn.cluster import KMeans
创建一个寻找数据中每个实例最接近的聚类中心的函数
def find_closest_centroids(X, centroids):
m = X.shape[0]
k = centroids.shape[0]
idx = np.zeros(m)
for i in range(m):
min_dist = 1000000
for j in range(k):
dist = np.sum((X[i,:] - centroids[j,:]) ** 2) # **:次方
if dist < min_dist:
min_dist = dist
idx[i] = j
return idx
创建计算簇的聚类中心的函数
聚类中心只是当前分配给簇的所有样本的平均值。
# 计算簇的聚类中心
def compute_centroids(X, idx, k):
m, n = X.shape
centroids = np.zeros((k, n))
for i in range(k):
indices = np.where(idx == i)
centroids[i,:] = (np.sum(X[indices,:], axis=1) / len(indices[0])).ravel()
return centroids
创建一个函数运行该算法的一些迭代次数和可视化结果
我们只需要在将样本分配给最近的簇并重新计算簇的聚类中心
# 运行该算法的一些迭代次数和可视化
def run_k_means(X, initial_centroids, max_iters):
m, n = X.shape
k = initial_centroids.shape[0]
idx = np.zeros(m)
centroids = initial_centroids
for i in range(max_iters):
idx = find_closest_centroids(X, centroids)
centroids = compute_centroids(X, idx, k)
return idx, centroids
可视化聚类结果
# 加载数据并随机选择聚类中心
data = loadmat('ex7data2.mat')
X = data['X']
initial_centroids = initial_centroids = np.array([[3, 3], [6, 2], [8, 5]])
idx = find_closest_centroids(X, initial_centroids)
# 将样本分配给最近的簇并重新计算簇的聚类中心
idx, centroids = run_k_means(X, initial_centroids, 10)
cluster1 = X[np.where(idx == 0)[0],:]
cluster2 = X[np.where(idx == 1)[0],:]
cluster3 = X[np.where(idx == 2)[0],:]
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(cluster1[:,0], cluster1[:,1], s=30, color='r', label='Cluster 1')
ax.scatter(cluster2[:,0], cluster2[:,1], s=30, color='g', label='Cluster 2')
ax.scatter(cluster3[:,0], cluster3[:,1], s=30, color='b', label='Cluster 3')
ax.legend()
plt.show()
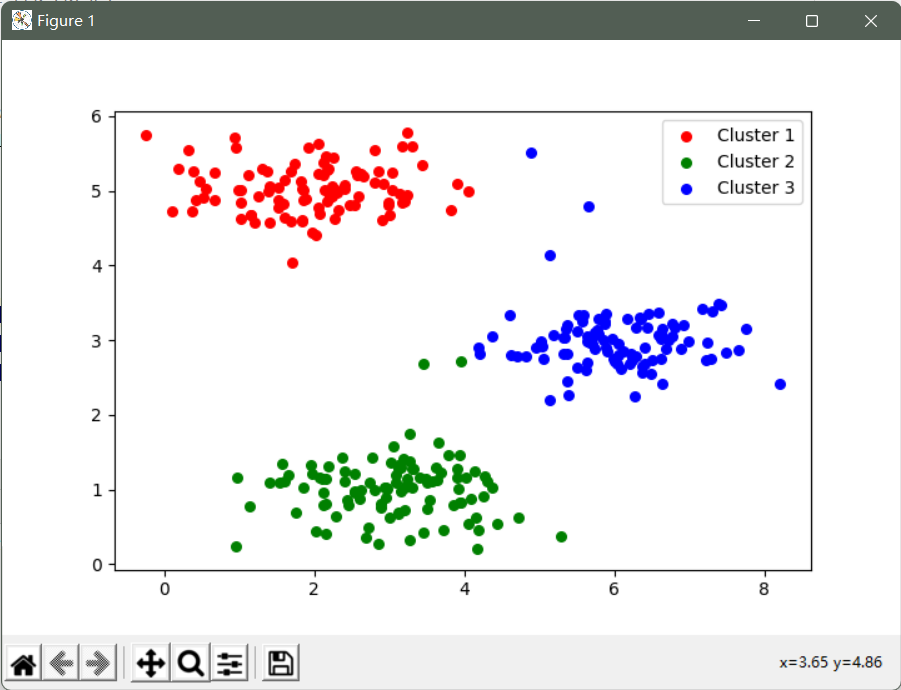
因为我们的聚类中心是随便选的, 所以可能会影响算法的收敛。
所以我们要创建一个选择随机样本并将其用作初始聚类中心的函数。
# 创建一个选择随机样本并将其用作初始聚类中心的函数
def init_centroids(X, k):
m, n = X.shape
centroids = np.zeros((k, n))
idx = np.random.randint(0, m, k)
for i in range(k):
centroids[i,:] = X[idx[i],:]
return centroids
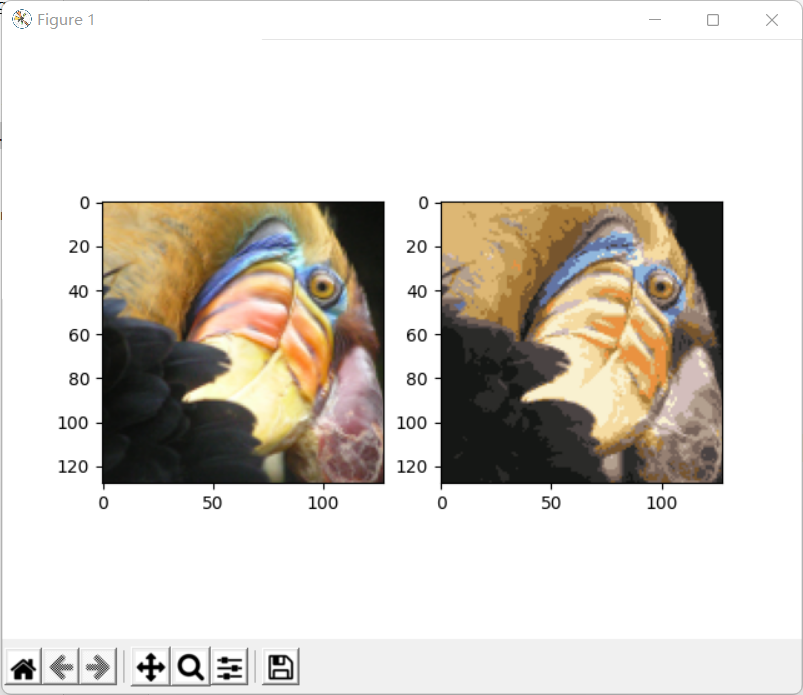
我们的下一个任务是将K-means应用于图像压缩。
我们可以使用聚类来找到最具代表性的少数颜色,并使用聚类分配将原始的24位颜色映射到较低维的颜色空间。
加载要压缩的图像,对数据应用一些预处理,并将其提供给K-means算法
# K-means图像压缩
# 使用聚类来找到最具代表性的少数颜色,并使用聚类分配将原始的24位颜色映射到较低维的颜色空间
# 原始像素数据已经为我们预加载,所以让我们把它拉进来
image_data = loadmat('bird_small.mat')
A = image_data['A']
# 对数据应用一些预处理,并将其提供给K-means算法
# 标准化值范围
A = A /255
# 重塑阵列形状
X = np.reshape(A, (A.shape[0] * A.shape[1], A.shape[2]))
运行K-means算法,并查看压缩后的图像
# 随机初始化质心
initial_centroids = init_centroids(X, 16)
# 运行算法
idx, centroids = run_k_means(X, initial_centroids, 10)
# 最后一次获取最近的质心
idx = find_closest_centroids(X, centroids)
# 将每个像素映射到质心值
X_recovered = centroids[idx.astype(int),:]
# 重塑为原始尺寸
X_recovered = np.reshape(X_recovered, (A.shape[0], A.shape[1], A.shape[2]))
# 可视化
plt.imshow(X_recovered)
plt.show()
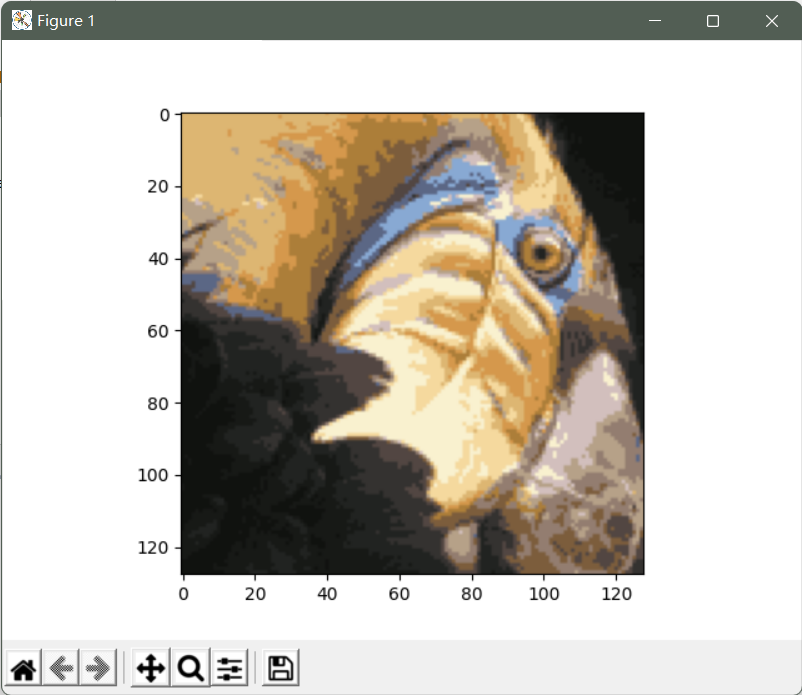
可以看到我们对图像进行了压缩,但图像的主要特征仍然存在。 这就是K-means。
我们还可以使用scikit-learn来实现K-means
# 使用scikit-learn来实现K-means
#标准化,使得像素数据为0-1之间
pic = io.imread('bird_small.png') / 255
# 序列化数据
data = pic.reshape(128*128, 3)
model = KMeans(n_clusters=16, n_init=100, n_jobs=-1)
# 先fit,再predict,然后再分配标记的聚类中心的RGB编码
model.fit(data)
centroids = model.cluster_centers_
C = model.predict(data)
compressed_pic = centroids[C].reshape((128,128,3))
# 绘图,对比图像
fig, ax = plt.subplots(1, 2)
ax[0].imshow(pic)
ax[1].imshow(compressed_pic)
plt.show()
Principal component analysis(主成分分析)
一、作业内容
首先用一个二维的样本集来实验,对PCA如何运行的有一个直观的感受,然后再在一个更大的由5000个人脸图像组成的数据集上实现PCA。
二、作业分析
1、降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。在实际的生产和应用中,降维在一定的信息损失范围内,可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。
2、降维具有如下一些优点:
(1) 使得数据集更易使用。
(2) 降低算法的计算开销。
(3) 去除噪声。
(4) 使得结果容易理解。
3、降维应用:
(1) 数据压缩
降维首先是可以用于数据压缩的,例如将2维数据降维成一维数据,就可以将存储量减小一半。
(2) 可视化
降维还可以将原本无法可视化的数据通过降维从而进行可视化。例如当特征较多,无法进行可视化,通过降维成二维数据,就可以进行可视化了。
4、PCA(Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
5、PCA特征降维步骤:
(1) 数据预处理(均值归一化/特征缩放feature scaling)
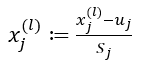
(2) 计算协方差矩阵
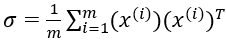
(3) 通过SVD函数计算出协方差σ的特征向量
[U, S, V] = svd(sigma)
(4) 从U矩阵中取出 u ( 1 ) u^{(1)} u(1)~ u ( k ) u^{(k)} u(k),从而构建新的矩阵(n*k的矩阵),称为 U r e d u c e U_{reduce} Ureduce
(5) 将n维的x降成k维的z,其中z= ( U r e d u c e ) T (U_{reduce})^T (Ureduce)TX
6、选择主成分K的数量:
(1) PCA算法主要做的工作就是最小化average squard projection error,也就是要最小化下面这个表达式:
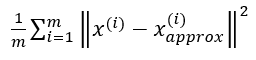
(2) 同时,我们还需要定义total variation(可以理解为样本和全零点之间的举例),也就是下面这个表达式:
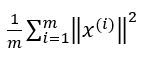
(3) 选择下面不等式成立的最小k
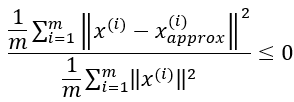
上式就表示百分之99的方差被保留了下来
7、PCA算法在较少数据维度的应用:
将原本高维度的数据x降至低维度的z,然后采用z建立模型进行训练
注意:
(1) PCA算法只能运行在训练集上,在交叉验证集或测试集中同样也是使用训练集建立的映射。(也就是在后面进行预测时要使用测试集计算出来的 U r e d u c e U_{reduce} Ureduce)
(2) 不要使用PCA去防止过拟合,因此PCA可能会损失一些重要的特征,使用正则化的方法去防止过拟合更有效果
(3) 如果能够在不使用PCA的情况下计算得到结果,那么就不要使用PCA。如果没办法计算得到(运行性太慢等等情况),再使用PCA。
三、代码实战
PCA是在数据集中找到“主成分”或最大方差方向的线性变换。 它可以用于降维。 在本练习中,我们首先负责实现PCA并将其应用于一个简单的二维数据集,以了解它是如何工作的。
引入所需函数库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
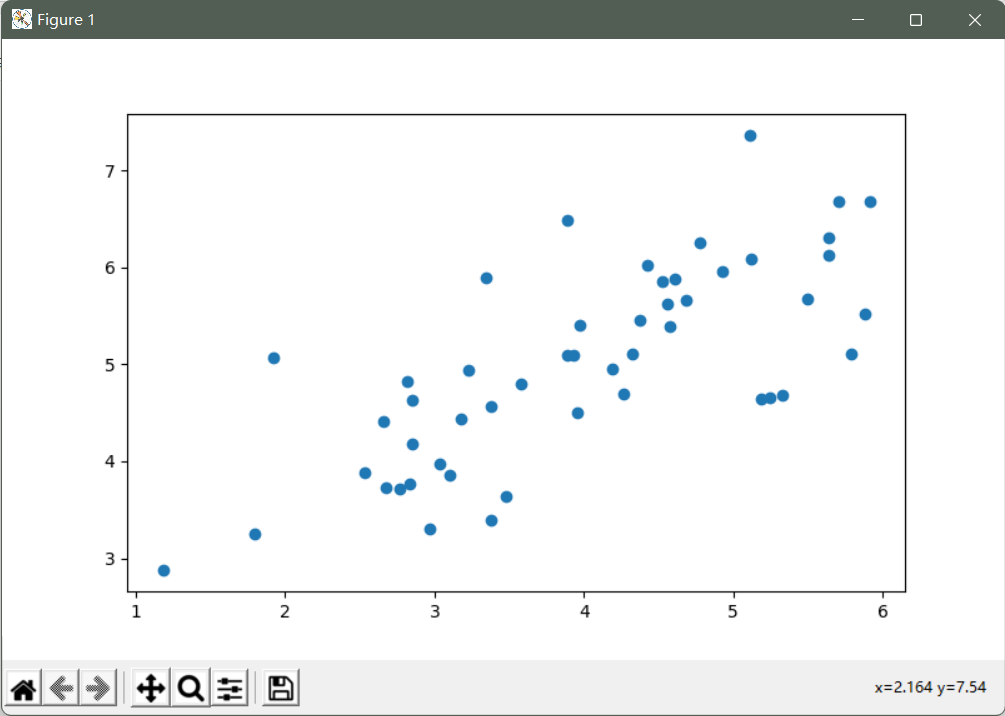
加载数据并绘图查看数据分布
data = loadmat('ex7data1.mat')
X = data['X']
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(X[:, 0], X[:, 1])
plt.show()
PCA算法在确保数据被归一化之后,输出仅仅是原始数据的协方差矩阵的奇异值分解
def pca(X):
# 规范化特征
X = (X - X.mean()) / X.std()
# 计算协方差矩阵
X = np.matrix(X)
cov = (X.T * X) / X.shape[0]
# 执行SVD
U, S, V = np.linalg.svd(cov)
return U, S, V
现在我们有主成分(矩阵U),我们可以用这些来将原始数据投影到一个较低维的空间中
实现一个计算投影并且仅选择顶部K个分量的函数,有效地减少了维数。
# 计算投影并且仅选择顶部K个分量的函数
def project_data(X, U, k):
U_reduce = U[:,:k]
return np.dot(X, U_reduce)
通过反向转换步骤来恢复原始数据
# 通过反向转换步骤来恢复原始数据
def recover_data(Z, U, k):
U_reduce = U[:,:k]
return np.dot(Z, U_reduce.T)
绘制出原始数据和还原后数据的分布图像
# 主成分(矩阵U)
U, S, V = pca(X)
# 将原始数据投影到较低维的空间中,将实现一个计算投影并且仅选择顶部K个分量的函数,有效地减少了维数
Z = project_data(X, U, 1)
# 通过反向转换步骤来恢复原始数据
X_recovered = recover_data(Z, U, 1)
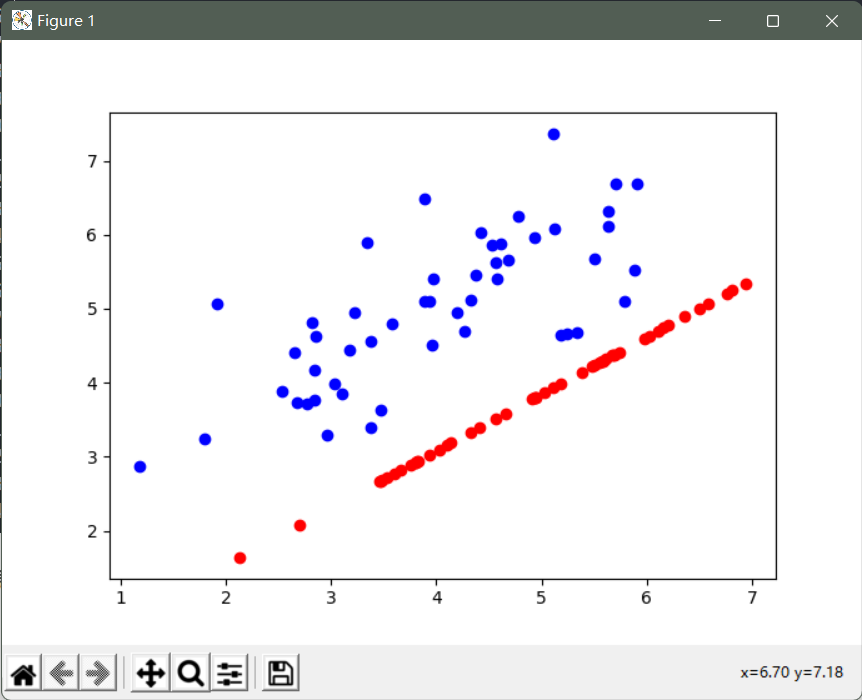
# 第一主成分的投影轴基本上是数据集中的对角线
# 当我们将数据减少到一个维度时,我们失去了该对角线周围的变化
# 所以在我们的再现中,一切都沿着该对角线
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(X[:, 0], X[:, 1], color='b') # 打印原始数据
ax.scatter(list(X_recovered[:, 0]), list(X_recovered[:, 1]), color='r') # 打印还原后的数据
plt.show()
后一个任务是将PCA应用于脸部图像。
通过使用相同的降维技术,我们可以使用比原始图像少得多的数据来捕获图像的“本质”。
创建一个将渲染数据集中的前100张脸的函数
def plot_n_image(X, n):
# 打印前n个图像
# n必须是一个平方数
pic_size = int(np.sqrt(X.shape[1]))
grid_size = int(np.sqrt(n))
first_n_images = X[:n, :]
fig, ax_array = plt.subplots(nrows=grid_size, ncols=grid_size, sharey=True, sharex=True)
for r in range(grid_size):
ax_array[r, c].imshow(first_n_images[grid_size * r + c].reshape((pic_size, pic_size)))
plt.xticks(np.array([]))
plt.yticks(np.array([]))
在面数据集上运行PCA,并取得前100个主要特征
faces = loadmat('ex7faces.mat')
X = faces['X']
U, S, V = pca(X)
Z = project_data(X, U, 100)
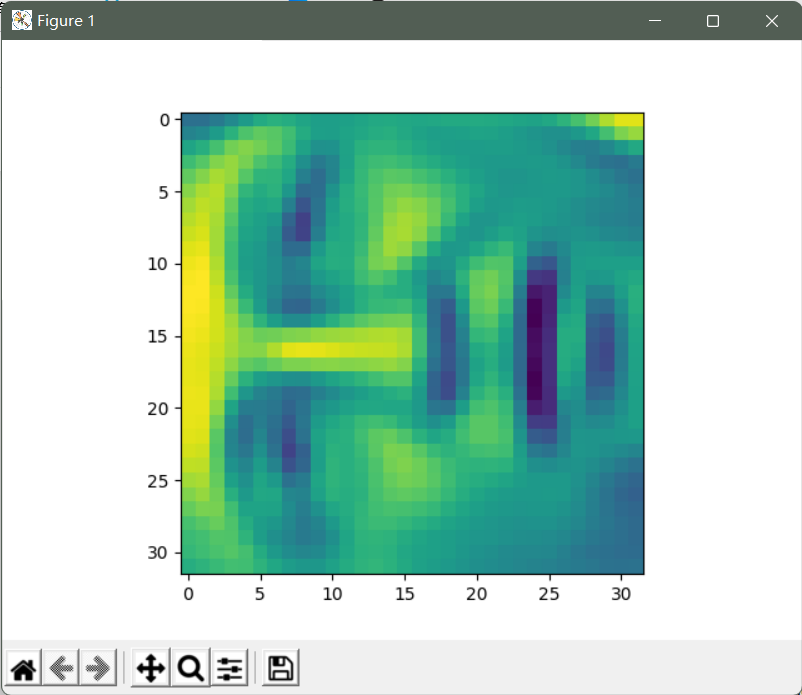
恢复原来的结构并再次渲染
X_recovered = recover_data(Z, U, 100)
face = np.reshape(X_recovered[3,:], (32, 32))
plt.imshow(face)
plt.show()
参考链接:https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
https://blog.csdn.net/m0_51933492/article/details/123927269?spm=1001.2014.3001.5502
https://blog.csdn.net/weixin_41799019/article/details/118418194?spm=1001.2014.3001.5502





















 4400
4400











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








