
1. 摘要
这项工作开发的图数据的Mixup。Mixup通过在两个随机样本之间插入特征和标签来提高神经网络的泛化和鲁棒性。传统上,Mixup可以处理常规的、类似的网格的欧几里得数据,比如图像或者表格数据。然而,直接采用Mixup对图数据进行增强具有挑战性,因为不同的图通常有以下几个问题:1)节点数量不同;2)不容易对齐;3)在非欧几里得空间中具有独特的类型学。为此,我们提出G-Mixup,通过插入不同类别图的生成器(即graphon)来增强图的分类。具体来说,我们首先使用同一个类中的图来估计graphon。然后,我们不直接操作图,而是在欧氏空间中插入不同类别的graphons,以得到混合graphons,其中合成图是通过基于graphons的采样生成的。大量实验表明,G-Mixup显著提高了GNNs的泛化能力和鲁棒性。
2. 动机
- 现有的图数据增强方法主要关注于图内的边和节点,不同实例之间的图间增强方法尚未得到充分开发。
- 能否将Mixup的思想应用于图数据?
存在的问题
1. 图数据是不规则的,不同图中节点的数量通常是不同的;
2. 图数据不对齐,图中的节点没有自然排序,很难匹配不同图之间的节点;
3. 类之间的图拓扑是发散的,来自不同类的一对图的拓扑通常是不同的,而来自同一类的一对图的拓扑通常是相似的。
3. 主要贡献
- 提出了G-Mixup来增强图分类的训练图。由于直接混合图是很难的,G-Mixup混合不同类型图的graphon来生成合成图;
- 从理论上证明了合成图将是原始图的混合,其中源图的关键拓扑(即判别主体)将混合在一起;
- 在各种图神经网络和数据集上证明了G-Mixup的有效性。
4. 定义
4.1 符号定义
给定图 G G G用 V ( G ) V(G) V(G)和 E ( G ) E(G) E(G)分别表示节点和边。节点和边的数量分别用 v ( G ) = ∣ V ( G ) ∣ v(G)=|V(G)| v(G)=∣V(G)∣和 e ( G ) = ∣ E ( G ) ∣ e(G)=|E(G)| e(G)=∣E(G)∣表示。用 m 、 l m、l m、l表示图的数量, N 、 K N、K N、K表示节点数量,用 G , H , I G,H,I G,H,I表示图或者图集。 y G ∈ R C y_G\in R^C yG∈RC表示图集 G G G的标签,其中 C C C为图的类数。一个图可以包含一些频繁的子图,这些子图被称为主体。图 G G G中的主体表示为 F G F_G FG。图集 G G G中的母题集记为 F G F_G FG。 W G W_G WG表示图集 G G G的graphon, W W W表示步长函数。 G ( K , W ) G(K, W) G(K,W)表示基于graphon W W W的包含 K K K个节点的随机图。
4.2 图同态和Graphons
图同态: 图同态是两个图之间的邻接保持映射,即将一个图中的邻接顶点映射到另一个图中的邻接顶点。形式化上,一个图同态
ϕ
:
F
→
G
\phi : F \rightarrow G
ϕ:F→G是
V
(
F
)
V(F)
V(F)到
V
(
G
)
V(G)
V(G)的映射,其中如果
{
u
,
v
}
∈
E
(
F
)
\{u,v\}\in E(F)
{u,v}∈E(F)那么
{
ϕ
(
u
)
,
ϕ
(
v
)
}
∈
E
(
G
)
\{\phi(u),\phi(v)\}\in E(G)
{ϕ(u),ϕ(v)}∈E(G)。对于两个图
H
H
H和
G
G
G,它们之间可能存在多个图同态。设
h
o
m
(
H
,
G
)
hom(H, G)
hom(H,G)表示图
H
H
H到图
G
G
G同态的总数。例如,
H
H
H是一个点
h
o
m
(
H
,
G
)
=
∣
V
(
G
)
∣
hom(H,G)=|V(G)|
hom(H,G)=∣V(G)∣,如果
H
H
H是一条边上的两个点
h
o
m
(
H
,
G
)
=
2
∣
E
(
G
)
∣
hom(H,G)=2|E(G)|
hom(H,G)=2∣E(G)∣,如果
H
H
H是一个三角形上的顶点,那么
h
o
m
(
H
,
G
)
hom(H,G)
hom(H,G)是
G
G
G中三角形数量的6倍。
H
H
H到
G
G
G的映射总共有
∣
V
(
G
)
∣
∣
V
(
H
)
∣
|V(G)|^{|V(H)|}
∣V(G)∣∣V(H)∣,但只有部分是同态的。因此,我们定义同态密度来测量图
H
H
H在图
G
G
G中出现的相对频率,即
t
(
H
,
G
)
=
h
o
m
(
H
,
G
)
∣
V
(
G
)
∣
∣
V
(
H
)
∣
t(H,G)=\frac{hom(H,G)}{|V(G)|^{|V(H)|}}
t(H,G)=∣V(G)∣∣V(H)∣hom(H,G)。例如,

Graphons: graphon是一个连续的、有界的对称函数 W : [ 0 , 1 ] 2 → [ 0 , 1 ] W:[0,1]^2\rightarrow[0,1] W:[0,1]2→[0,1],可以认为是具有无限个节点的图的权矩阵。那么,给定两点 u i , u j ∈ [ 0 , 1 ] , W ( i , j ) u_i,u_j\in[0,1],W(i,j) ui,uj∈[0,1],W(i,j)表示节点 i i i和 j j j与一条边相关的概率。图的不同量可以用graphon的函数来计算。例如,图中节点的度可以很容易地扩展为图中的度分布函数,其特征是图的边缘 d W ( x ) = ∫ 0 1 W ( x , y ) d y d_W(x)=\int_0^1W(x,y)d_y dW(x)=∫01W(x,y)dy。同样,同态密度的概念也可以自然地从图扩展到graphons。给定一个任意图主体 F F F,其关于graphon W W W的同态密度由 t ( F , W ) = ∫ [ 0 , 1 ] V ( F ) ∏ i , j ∈ E ( F ) W ( x i , x j ) ∏ i ∈ V ( F ) d x i t(F,W)=\int_{[0,1]^{V(F)}} \prod_{i,j\in E(F)}W(x_i,x_j)\prod_{i\in V(F)}dx_i t(F,W)=∫[0,1]V(F)∏i,j∈E(F)W(xi,xj)∏i∈V(F)dxi。例如,graphon W W W的边密度是 ∫ [ 0 , 1 ] 2 W ( x , y ) d x d y \int_{[0,1]^2}W(x,y)dxdy ∫[0,1]2W(x,y)dxdy,graphon W W W的三角形密度为 ∫ [ 0 , 1 ] 3 W ( x , y ) W ( x , z ) W ( y , z ) d x d y d z \int_{[0,1]^3}W(x,y)W(x,z)W(y,z)dxdydz ∫[0,1]3W(x,y)W(x,z)W(y,z)dxdydz
5. 方法

5.1 G-Mixup
G-Mixup对不同的图生成器进行插值,得到一个新的混合图生成器。然后,基于混合graphon对合成图进行采样,实现数据扩充。从该生成器中采样的图部分具有原始图的性质。形式上,G-Mixup的表达式为:

其中
W
G
,
W
H
W_G,W_H
WG,WH是图集
G
G
G和
H
H
H的graphons。混合graphon由
W
I
W_I
WI表示,
λ
∈
[
0
,
1
]
\lambda \in[0,1]
λ∈[0,1]是控制不同源集贡献的权值超参数。由
W
I
W_I
WI生成的合成图集合为
I
=
{
I
1
,
I
2
,
.
.
.
,
I
m
}
I=\{I_1,I_2,...,I_m\}
I={I1,I2,...,Im}。
y
G
∈
R
C
y_G \in R^C
yG∈RC和
y
H
∈
R
C
y_H\in R^C
yH∈RC分别是包含图
G
G
G和图
H
H
H的真实标签的向量,其中
C
C
C为类的数量。图集
I
I
I中合成图的标签向量记为
y
I
∈
R
C
y_I \in R^C
yI∈RC。
如图1和上面的方程所示,提出的G-Mixup包括三个关键步骤:1)为每一类图估计一个graphon,2)混合不同图类的graphons,3)基于混合graphons生成合成图。具体来说,假设我们有两个图集
G
=
{
G
1
,
G
2
,
.
.
.
,
G
m
}
G=\{G_1,G_2,...,G_m\}
G={G1,G2,...,Gm},标签为
y
G
y_G
yG,
H
=
{
H
1
,
H
2
,
.
.
.
,
H
m
}
H=\{H_1,H_2,...,H_m\}
H={H1,H2,...,Hm},标签为
y
H
y_H
yH。Graphons
W
G
W_G
WG和
W
H
W_H
WH分别从图集
G
G
G和
H
H
H中估计。然后,我们通过线性插值两个graphons及其标签将它们混合,得到
W
I
W_I
WI和
y
I
y_I
yI。最后,基于
W
I
W_I
WI对一组合成图
I
I
I进行采样,作为额外的训练图数据。
5.2 实现
Graphon估计和混合: graphon是一个未知函数,没有真实图形的封闭表达式。因此,我们使用阶梯函数来近似graphon。一般来说。阶梯函数可以看成是一个矩阵 W = [ w k k ′ ] ∈ [ 0 , 1 ] K × K W=[w_{kk'}]\in [0, 1]^{K×K} W=[wkk′]∈[0,1]K×K,其中 W i j W_{ij} Wij是节点 i i i和节点 j j j之间存在边的概率。在实践中,我们使用矩阵形式的阶梯函数作为graphon来混合并生成合成图。阶梯函数估计方法已经得到了很好的研究,该方法首先根据节点测量值(如度)对一组图中的节点进行对齐,然后从所有对齐的邻接矩阵中估计阶梯函数。典型的阶梯函数估计方法包括排序和平滑(SAS)方法,随机块逼近(SBA),“最大差距”(LG),矩阵完成(MC),通用奇异值阈值(USVT)。在形式上,一个阶梯函数 W P : [ 0 , 1 ] 2 → [ 0 , 1 ] W^P:[0,1]^2\rightarrow [0,1] WP:[0,1]2→[0,1]被定义为 W P ( x , y ) = ∑ k , k ′ = 1 K w k k ′ 1 P k × P k ′ ( x , y ) W^P(x,y)=\sum^K_{k,k'=1}w_{kk'}1_{P_k×P_{k'}}(x,y) WP(x,y)=∑k,k′=1Kwkk′1Pk×Pk′(x,y),其中 P = ( P 1 , . . . , P K ) P=(P_1,...,P_K) P=(P1,...,PK)表示将 [ 0 , 1 ] [0,1] [0,1]划分成长度为 1 / K , w k k ′ ∈ [ 0 , 1 ] 1/K,w_{kk'}\in[0,1] 1/K,wkk′∈[0,1]的 K K K个相邻区间,如果 ( x , y ) ∈ P k × P k ′ (x,y)\in P_k×P_{k'} (x,y)∈Pk×Pk′,则指示函数 1 P k × P k ′ = 1 1_{P_k×P_{k'}}=1 1Pk×Pk′=1,否则为0。对于二分类问题,我们有 G = { G 1 , G 2 , . . . , G m } G=\{G_1,G_2,...,G_m\} G={G1,G2,...,Gm}和 H = { H 1 , H 2 , . . . , H m } H=\{H_1,H_2,...,H_m\} H={H1,H2,...,Hm}具有不同的标签,我们估计他们的阶梯函数 W G ∈ R K × K W_G\in R^{K×K} WG∈RK×K和 W H ∈ R K × K W_H\in R^{K×K} WH∈RK×K,其中我们让 K K K为所有图中节点的平均数量。对于多类分类,我们首先估计每一类图的阶梯函数,然后随机选择两类图进行混合。所得的阶梯函数 W I = λ W G + ( 1 − λ ) W H ∈ R K × K W_I=\lambda W_G+(1-\lambda)W_H\in R^{K×K} WI=λWG+(1−λ)WH∈RK×K,作为合成图的生成器。
合成图生成: graphon
W
W
W提供了一个分布来生成任意大小的图。具体来说,
K
K
K节点随机图
G
(
K
,
W
I
)
G(K, W_I)
G(K,WI)的生成过程如下:

我们设
W
(
u
i
,
u
j
)
=
W
[
⌊
1
/
u
i
⌋
,
⌊
1
/
u
j
⌋
]
W(u_i,u_j)=W[\lfloor 1/u_i \rfloor,\lfloor 1/u_j \rfloor]
W(ui,uj)=W[⌊1/ui⌋,⌊1/uj⌋]。第一步在
[
0
,
1
]
[0,1]
[0,1]上独立于均匀分布
U
n
i
f
[
0
,
1
]
Unif_{[0,1]}
Unif[0,1]对K个节点进行采样。第二步生成邻接矩阵
A
=
[
a
i
j
]
∈
{
0
,
1
}
K
×
K
A = [a_{ij}]∈\{0,1\}^{K×K}
A=[aij]∈{0,1}K×K,其元素值遵循由阶梯函数确定的伯努利分布
B
e
r
n
(
⋅
)
Bern(·)
Bern(⋅)。由此得到一个图
G
G
G,其中
V
(
G
)
=
{
1
,
…
,
K
}
V(G) =\{1,…,K\}
V(G)={1,…,K}和
E
(
G
)
=
{
(
i
,
j
)
∣
a
i
j
=
1
}
E(G)=\{(i,j)|a_{ij}=1\}
E(G)={(i,j)∣aij=1}。通过多次执行上述过程,可以生成一组合成图。合成图节点特征的生成包括两个步骤:1)基于原始节点特征构建graphon节点特征,2)基于graphon节点特征生成合成图节点特征。
具体来说,在graphon估计阶段,我们在对齐邻接矩阵的同时对齐原始节点特征,因此我们对每个graphon都有一组对齐的原始节点特征,然后我们对对齐的原始节点特征进行池化(在我们的实验中是平均池化),获得图形节点特征。生成的图的节点特征与graphon特征相同。
6. 理论依据
定理6.1(判别主体)图 G G G的判别主体 F G F_G FG是节点和边数量最少的子图,它可以决定图 G G G的类, F G ′ F'_G FG′是集合 G ′ G' G′中图的判别主体的集合。直观地说,判别主体是图形的关键拓扑结构。假设(i)每个图 G G G都有一个判别主体 F G F_G FG,(ii)一组图 G ′ G' G′有一个有限的判别主体集合 F G ′ F'_G FG′。
6.1 λ W G + ( 1 − λ ) W H \lambda W_G + (1-\lambda)W_H λWG+(1−λ)WH中是否存在判别主体 F G F_G FG和 F H F_H FH?
定理6.2 给定两个图集 G G G和 H H H,对应的图形是 W G W_G WG和 W H W_H WH,对应的判别主体集合是 F G F_G FG和 F H F_H FH。对于每一个判别主体 F G ∈ F G ′ F_G \in F'_G FG∈FG′和 F H ∈ F H ′ F_H \in F'_H FH∈FH′,混合graphon W I = λ W G + ( 1 − λ ) W H W_I=\lambda W_G+(1-\lambda)W_H WI=λWG+(1−λ)WH中 F G / F H F_G/F_H FG/FH的同态密度差与graphon W H / W G W_H/W_G WH/WG的同态密度差的上界为
∣ t ( F G , W I ) − t ( F G , W G ) ∣ ≤ ( 1 − λ ) e ( F G ) ∣ ∣ W H − W G ∣ ∣ □ , ∣ t ( F H , W I ) − t ( F H , W H ) ∣ ≤ λ e ( F H ) ∣ ∣ W H − W G ∣ ∣ □ |t(F_G,W_I)-t(F_G,W_G)|\leq (1-\lambda)e(F_G)||W_H-W_G||_\square, \\ |t(F_H,W_I)-t(F_H,W_H)|\leq \lambda e(F_H)||W_H-W_G||_\square ∣t(FG,WI)−t(FG,WG)∣≤(1−λ)e(FG)∣∣WH−WG∣∣□,∣t(FH,WI)−t(FH,WH)∣≤λe(FH)∣∣WH−WG∣∣□
其中 e ( F ) e(F) e(F)是图 F F F的节点数, ∣ ∣ W H − W G ∣ ∣ □ ||W_H-W_G||_\square ∣∣WH−WG∣∣□表示切割规范。
定理4.2表明,混合graphon与原始graphon的同态密度差有上界。差异取决于超参数 λ λ λ、边数 e ( F G ) / e ( F H ) e(F_G)/e(F_H) e(FG)/e(FH)和切割规范 ∣ ∣ W H − W G ∣ ∣ □ ||W_H-W_G||_\square ∣∣WH−WG∣∣□。因为 e ( F G ) / e ( F H ) e(F_G)/e(F_H) e(FG)/e(FH)和切割规范 ∣ ∣ W H − W G ∣ ∣ □ ||W_H-W_G||_\square ∣∣WH−WG∣∣□是由数据集决定的(可以看作是一个常数),同态密度的差异将由 λ λ λ决定。在此基础上,将混合garphon的标签设为 λ y G + ( 1 − λ ) y H λy_G +(1−λ)y_H λyG+(1−λ)yH。因此,G-Mixup可以将两个不同graphon的不同鉴别图案保存到一个混合graphon中。
6.2 从graphon W I W_I WI生成的图形会保留混合的区别性图案吗?
定理6.3 设 W I W_I WI为混合graphon, n ≥ 1 , 0 < ε < 1 n \geq 1,0 < ε < 1 n≥1,0<ε<1, F I F_I FI为混合判别主体,则 W I W_I WI随机图 G = G ( n , W I ) G=G(n,W_I) G=G(n,WI)满足 P ( ∣ t ( F I , G ) − t ( F I , W I ) ∣ > ε ) ≤ 2 e x p ( − ε 2 n 8 v ( F I ) 2 ) P(|t(F_I,G)-t(F_I,W_I)|>ε)\leq 2exp(-\frac{ε^2n}{8v(F_I)^2}) P(∣t(FI,G)−t(FI,WI)∣>ε)≤2exp(−8v(FI)2ε2n)
定理4.3指出,对于任意指定的非零裕度 ε ε ε,当从混合graphon中采样足够数量的图时,合成图中判别主体的同态密度将以高概率近似等于graphon中 t ( F I , G ) ≈ t ( F I , W I ) t(F_I, G)≈t(F_I, W_I) t(FI,G)≈t(FI,WI)的同态密度。换句话说,如果样本数 n n n足够大,合成图将以非常高的概率保留混合graphon的判别主体。因此,G-Mixup可以将两个不同图的判别主体保留为一个混合图。
7. 实验结果

7.1 现实世界中不同类别的图有不同的graphons吗?
在图2中可视化了估计的图形。结果表明:同一数据集中不同类型的图的图形具有明显的差异。图2中IMDB-BINAERY的图形显示类1的图形有更大的密集区域,这表明该类图比类0的图有更大的群落。图2中的REDDIT-BINARY图显示类0的图有一个高度节点,而类1的图有两个高度节点。
7.2 G-Mixup在做什么?
在图3中可视化REDDIT-BINARY数据集中生成的合成图。我们观察到合成图确实是原始图的混合。原始图和生成的合成图分别显示在图3(a)(b)和图3©(d)(e)中。图3展示了混合graphon 0.5 ∗ W G + 0.5 ∗ W H 0.5 * W_G + 0.5 * W_H 0.5∗WG+0.5∗WH能够生成具有高度节点和密集子图的图,可以将其视为具有一个高度节点和两个高度节点的图的混合。它验证了G-Mixup更喜欢保留从原始图的判别主体。
7.3 G-Mixup能提高GNN的性能和泛化能力吗?


-
G-Mixup可以提高图神经网络在各种数据集上的性能。 从表2可以看出,G-Mixup在15个报道的准确度中获得了12个最佳性能,这大大提高了GNN的性能。总的来说,G-Mixup的性能比普通模型好2.84%。从表3可以看出,在8种情况下,G-Mixup获得了7个最佳性能,这大大提高了DiffPool和MincutPool的性能。
-
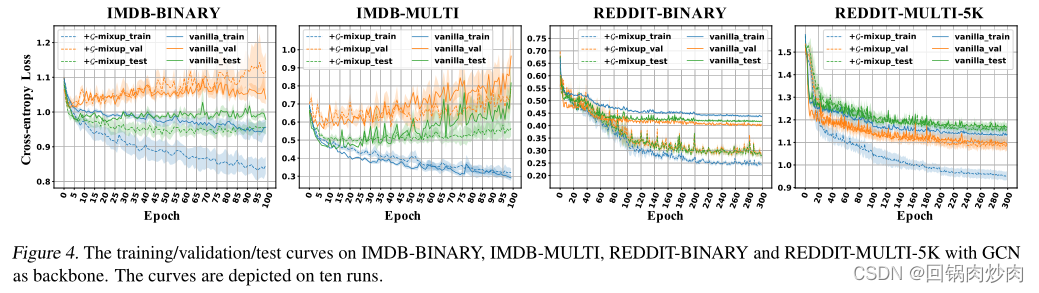
G-Mixup可以提高图神经网络的泛化能力。 从图4中测试数据的损失曲线(绿线)来看,G-Mixup的测试数据的损失(绿色虚线)始终低于普通模型(绿色实线)。考虑到GMixup具有更好的性能和更好的测试损耗曲线,它能够大大提高GNN的泛化性能。
-
G-Mixup能稳定模型训练。 如表2所示,G-Mixup在15个报告数据中比香草模型的标准偏差低了11个。此外,图4中G-Mixup的训练/验证/测试曲线(虚线)比香草模型(实线)更稳定,说明G-Mixup稳定了图神经网络的训练。
7.4 G-Mixup能提高GNN的鲁棒性吗?

G-Mixup提高了图神经网络的鲁棒性。 作者研究了G-Mixup的两种鲁棒性,分别是标签破坏鲁棒性和拓扑破坏鲁棒性,结果分别报告在表4和表5中。表4显示了G-Mixup总体上获得了更好的性能,表明它比普通基线更健壮。表5显示,当图拓扑损坏时,G-Mixup更健壮,因为准确性始终比基线更好。当图标签或拓扑有噪声时,这可能是G-Mixup的一个优势。
7.5 更多分析
7.5.1 生成图的节点数

作者研究了G-Mixup生成的合成图中节点数量的影响,结果显示在图5中。从图5中观察到G-Mixup中使用所有原始图的平均节点数的是超参数 K K K更好的选择
7.5.2 对更深层次模型的影响
G-Mixup改进了不同层次的图神经网络的性能。 作者研究了GCN深入时G-Mixup的性能。对不同的层数(2−9)进行实验,结果显示在图6中。在图6中,左边的图显示当GCNs的深度为2−6时,G-Mixup的性能更好。深度GCNs(7−9)的性能与基线相当,但精度远低于浅层GCNs。右边的图显示,当GCNs深度为2−9时,G-Mixup的性能显著提高。这验证了G-Mixup在图神经网络深入研究时的有效性。







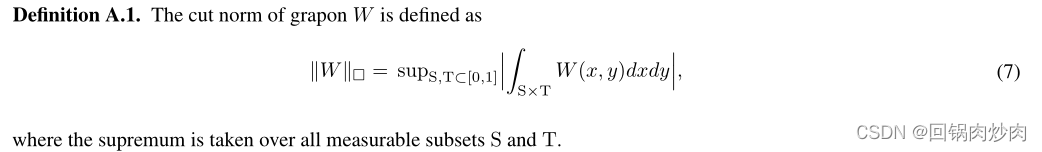
















 753
753

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








