【牛客 11259H】Scholomance Academy——生成函数、分治NTT、Bostan-mori 算法

【牛客 11259H】Scholomance Academy

题目描述

不知道是改的题面还是真的原题

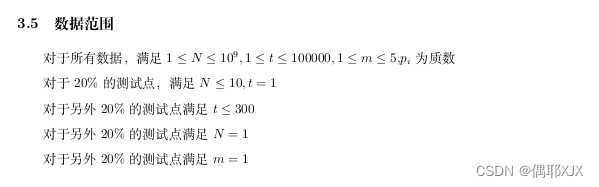
题解

本来是想拿部分分跑路的，但是这题的部分分提示也太给力了！

首先考虑 $t=1$ 的情况，乘法转换成指数上的加法，相当于把 $N$ 拆成 $m$ 个数 $a_1,a_2,...,a_m$ 相加，然后求 ${\prod }_{i=1}^m\phi (p^{a_i})$ 的和。

不妨设 $f_p(x)$ 为欧拉函数在质数 $p$ 的指数上的生成函数，即满足 $\phi (p^k)=[x^k]f_p(x)$。
答案显然是个加法卷积，所以我们要求的就是 $[x^N](f_p(x){)}^m$。

顺着这个思路，我们把 $f_p(x)$ 化简：
$$\begin{gathered} f_p(x)=1+(p-1)x+(p-1)p{x}^2+... \\ =\frac{1}{p}+\frac{p-1}{p}\cdot \frac{1}{1-px}=\frac{1-x}{1-px} \\ Ans=[x^N](\frac{1-x}{1-px}{)}^m \end{gathered}$$所以，如果 $N$ 特别大的话，我们可以用求解分式远项的 Bostan-mori 算法轻松解决。

然后考虑 $t>1$ 的情况，由于 $p_i$ 互不相同，积性函数可以直接相乘，所以答案的生成函数就是
$$\prod _{i=1}^t(\frac{1-x}{1-p_{i}x}{)}^m=\frac{(1-x{)}^{tm}}{{\prod }_{i=1}^t(1-p_{i}x{)}^m}$$上面部分可以直接用点值+快速幂 $O(tm\log tm)$ 求出来，下面部分可以用分治NTT $O(tm{\log }^{2}tm)$ 求出。

最后直接上 Bostan-mori 算法求第 $N$ 项，复杂度 $O(tm\log tm\log N)$。

代码

#include<bits/stdc++.h>//JZM yyds!!
#define ll long long
#define lll __int128
#define uns unsigned
#define fi first
#define se second
#define IF (it->fi)
#define IS (it->se)
#define END putchar('\n')
#define lowbit(x) ((x)&-(x))
#define inline jzmyyds
using namespace std;
const int MAXN=1<<20|5;
const ll INF=1e17;
ll read(){
	ll x=0;bool f=1;char s=getchar();
	while((s<'0'||s>'9')&&s>0){if(s=='-')f^=1;s=getchar();}
	while(s>='0'&&s<='9')x=(x<<1)+(x<<3)+(s^48),s=getchar();
	return f?x:-x;
}
int ptf[50],lpt;
void print(ll x,char c='\n'){
	if(x<0)putchar('-'),x=-x;
	ptf[lpt=1]=x%10;
	while(x>9)x/=10,ptf[++lpt]=x%10;
	while(lpt>0)putchar(ptf[lpt--]^48);
	if(c>0)putchar(c);
}
const ll MOD=998244353;
ll ksm(ll a,ll b,ll mo){
	ll res=1;
	for(;b;b>>=1,a=a*a%mo)if(b&1)res=res*a%mo;
	return res;
}
#define g 3ll
int rev[MAXN<<1],omg[MAXN<<1];
int NTT(ll*a,int N,int inv){
	int bit=1,n=N;
	while((1<<bit)<n)bit++;
	for(int i=0,lm=n=(1<<bit);i<lm;i++){
		rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
		if(i<rev[i])swap(a[i],a[rev[i]]);
	}ll x,y,tmp;omg[0]=1;
	for(int m=1,mi=(MOD-1)>>1;m<n;m<<=1,mi>>=1){
		tmp=ksm(g,inv>0?mi:MOD-1-mi,MOD);
		for(int i=1;i<m;i++)omg[i]=omg[i-1]*tmp%MOD;
		for(int i=0,om;i<n;i+=(m<<1),om=0)for(int j=i;j<i+m;j++,om++)
			x=a[j],y=a[j+m]*omg[om]%MOD,a[j]=(x+y)%MOD,a[j+m]=(x-y+MOD)%MOD;
	}if(inv<0)for(int i=0,iv=ksm(n,MOD-2,MOD);i<n;i++)(a[i]*=iv)%=MOD;
	return n;
}
#undef g

int n,k,m,p[MAXN];
ll P[MAXN<<1],Q[MAXN<<1],f[MAXN<<1];

int solve(int l,int r){
	if(l==r)return Q[0]=1,Q[1]=MOD-p[l],2;
	int mid=(l+r)>>1;
	int m1=solve(l,mid),len=(r-l+2),h=1;
	while(h<len)h<<=1;
	ll g[h];
	memset(g,0,sizeof(g));
	for(int i=0;i<m1;i++)g[i]=Q[i];
	int m2=solve(mid+1,r);
	for(int i=m2;i<h;i++)Q[i]=0;
	NTT(g,h,1),NTT(Q,h,1);
	for(int i=0;i<h;i++)(Q[i]*=g[i])%=MOD;
	NTT(Q,h,-1);
	return len;
}
int main()
{
	freopen("math.in","r",stdin);
	freopen("math.out","w",stdout);
	k=read(),n=read(),m=read();
	for(int i=1;i<=n;i++)p[i]=read();
	int lq=solve(1,n),lp=lq*m;
	P[0]=1,P[1]=MOD-1;
	int h=NTT(P,lp,1);
	for(int i=0;i<h;i++)P[i]=ksm(P[i],n*m,MOD);
	NTT(P,lp,-1);
	for(int i=lq;i<h;i++)Q[i]=0;
	NTT(Q,lq=lp,1);
	for(int i=0;i<h;i++)Q[i]=ksm(Q[i],m,MOD);
	NTT(Q,lq,-1),m=k;
	int N=1;n=lp-1;
	while(N<(n<<1|1))N<<=1;
	for(;m;m>>=1){
		for(int i=0;i<=n;i++)f[i]=(i&1)?(MOD-Q[i])%MOD:Q[i];
		for(int i=n+1;i<N;i++)f[i]=0;
		NTT(f,N,1),NTT(P,N,1),NTT(Q,N,1);
		for(int i=0;i<N;i++)(P[i]*=f[i])%=MOD,(Q[i]*=f[i])%=MOD;
		NTT(P,N,-1),NTT(Q,N,-1);
		for(int i=0;i<=n;i++)Q[i]=Q[i<<1];
		for(int i=n+1;i<N;i++)Q[i]=0;
		for(int i=0;i<=n;i++)P[i]=P[i<<1|(m&1)];
		for(int i=n+1;i<N;i++)P[i]=0;
	}
	print(P[0]*ksm(Q[0],MOD-2,MOD)%MOD);
	return 0;
}