【NOI模拟赛】废物题（快速沃尔什变换，分治NTT）

背景

 ____
/====\
|X  O|R    dp[i⊕j] += A[i] × B[j]
\ ++ /`
 |``|

异演顶针，鉴定为：废(F)物(W)题(T)

题面

给出 $n$ 个 $0$ 到 $K-1$ 之间的整数，对于每个 $i\in [0,K)$ 求从中选 $m$ 个使得异或和为 $i$ 的方案数对 $998244353$ 取模。

$1\le m\le n<130000,K=2^k,k\le 17$ .

题解

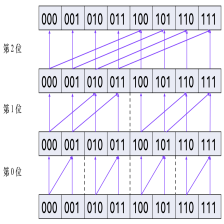
如背景里所说，这题应该是个用FWT处理异或卷积的题。

我们将每个数进行异或正变换后，题目等价于将 $n$ 个数组选 $m$ 个每一位乘起来起来，再相加。完了最后再逆变换回去。

每一位是独立的，且每个正变换后的数组只含有 1 和 -1，每一位的所有 1 和 -1 都没有区别。所以，我们可以直接用 1 和 -1 的数量来刻画每一位的情况。

1 和 -1 总数为 n ，我们把所有数放在一起进行正变换，又可以得到每个位置上 1 和 -1 的和，于是，就可以得到 1 和 -1 分别的数量。这个过程做一次 FWT。

假设某个位置 1 的数量为 $a$ ，那么这个位置逆变换前的数就是 $[x^m](1+x{)}^a(1-x{)}^{n-a}$ 。

我们可以用分治 NTT 做，具体地，分治时一段长度 $L$ 的区间，我们只需要记录多项式的 $(m-L)\sim m$ 位就好了。总时间复杂度 $O(n{\log }^{2}n+K\log K)$ 。

CODE

#include<map>
#include<set>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<random>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN (1<<17|5)
#define LL long long
#define ULL unsigned long long
#define ENDL putchar('\n')
#define DB double
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
int xchar() {
	static const int maxn = 1000000;
	static char b[maxn];
	static int pos = 0,len = 0;
	if(pos == len) pos = 0,len = fread(b,1,maxn,stdin);
	if(pos == len) return -1;
	return b[pos ++];
}
//#define getchar() xchar()
LL read() {
	LL f = 1,x = 0;int s = getchar();
	while(s < '0' || s > '9') {if(s<0)return -1;if(s=='-')f=-f;s = getchar();}
	while(s >= '0' && s <= '9') {x = (x<<1) + (x<<3) + (s^48);s = getchar();}
	return f*x;
}
void putpos(LL x) {if(!x)return ;putpos(x/10);putchar((x%10)^48);}
void putnum(LL x) {
	if(!x) {putchar('0');return ;}
	if(x<0) putchar('-'),x = -x;
	return putpos(x);
}
void AIput(LL x,int c) {putnum(x);putchar(c);}

const int MOD = 998244353;
const int inv2 = (MOD+1)/2;
int n,m,s,o,k;
int fac[MAXN],inv[MAXN],invf[MAXN];
int C(int n,int m) {
    if(m < 0 || m > n) return 0;
    return fac[n] *1ll* invf[n-m] % MOD * invf[m] % MOD;
}
int a[MAXN];
int MD(int x) {if(x>=MOD)x-=MOD;return x;}
void FWTXOR(int *s,int n) {
    for(int k = 2;k <= n;k <<= 1) {
        for(int j = 0;j < n;j += k) {
            for(int i = j;i < j+(k>>1);i ++) {
                int A = s[i],B = s[i+(k>>1)];
                s[i] = MD(A +MOD- B);
                s[i+(k>>1)] = MD(A + B);
            }
        }
    }return ;
}
void IFWTXOR(int *s,int n) {
    for(int k = n;k > 1;k >>= 1) {
        for(int j = 0;j < n;j += k) {
            for(int i = j;i < j+(k>>1);i ++) {
                int A = s[i],B = s[i+(k>>1)];
                s[i] = (A + B) *1ll* inv2 % MOD;
                s[i+(k>>1)] = (B +MOD- A) *1ll* inv2 % MOD;
            }
        }
    }return ;
}
int qkpow(int a,int b) {
    int res = 1;
    while(b > 0) {
        if(b & 1) res = res *1ll* a % MOD;
        a = a *1ll* a % MOD; b >>= 1;
    }return res;
}
int xm[MAXN<<2],om,rev[MAXN<<2];
void NTT(int *s,int n,int op) {
    for(int i = 1;i < n;i ++) {
        rev[i] = ((rev[i>>1]>>1) | ((i&1) ? (n>>1):0));
        if(rev[i] < i) swap(s[rev[i]],s[i]);
    }
    om = qkpow(3,(MOD-1)/n); xm[0] = 1;
    if(op < 0) om = qkpow(om,MOD-2);
    for(int i = 1;i <= n;i ++) xm[i] = xm[i-1] *1ll* om % MOD;
    for(int k = 2,t = n>>1;k <= n;k <<= 1,t >>= 1) {
        for(int j = 0;j < n;j += k) {
            for(int i = j,l = 0;i < j+(k>>1);i ++,l += t) {
                int A = s[i],B = s[i+(k>>1)];
                s[i] = (A + B*1ll*xm[l]) % MOD;
                s[i+(k>>1)] = (A +MOD- B*1ll*xm[l]%MOD) % MOD;
            }
        }
    }
    if(op < 0) {
        int iv = qkpow(n,MOD-2);
        for(int i = 0;i < n;i ++) s[i] = s[i] *1ll* iv % MOD;
    }return ;
}
int dp[MAXN];
int A[MAXN<<2],B[MAXN<<2];
void solve(int l,int r,int st) {
    // cerr<<l<<" "<<r<<endl;
    if(l == r) {
        dp[l] = (A[m-st] + A[m-st-1]) % MOD;
        return ;
    }
    int nn = m-st;
    vector<int> q; q.resize(nn+1);
    for(int i = 0;i <= nn;i ++) q[i] = A[i];
    int md = (l + r) >> 1,rn = r-md,le = 1,ln = md-l+1;
    while(le <= rn+nn) le <<= 1;
    for(int i = rn+1;i < le;i ++) B[i] = 0;
    for(int i = nn+1;i < le;i ++) A[i] = 0;
    for(int i = 0;i <= rn;i ++) B[i] = (i&1) ? (MOD-C(rn,i)):C(rn,i);
    NTT(A,le,1); NTT(B,le,1);
    for(int i = 0;i < le;i ++) A[i] = A[i] *1ll* B[i] % MOD;
    NTT(A,le,-1);
    int sl = max(0,m-ln);
    for(int i = 0;i <= m-sl;i ++) A[i] = A[i+sl-st];
    solve(l,md,sl);
    le = 1; while(le <= ln+nn) le <<= 1;
    for(int i = 0;i < le;i ++) B[i] = A[i] = 0;
    for(int i = 0;i <= nn;i ++) A[i] = q[i];
    for(int i = 0;i <= ln;i ++) B[i] = C(ln,i);
    NTT(A,le,1); NTT(B,le,1);
    for(int i = 0;i < le;i ++) A[i] = A[i] *1ll* B[i] % MOD;
    NTT(A,le,-1);
    int sr = max(0,m-rn);
    for(int i = 0;i <= m-sr;i ++) A[i] = A[i+sr-st];
    solve(md+1,r,sr);
    return ;
}
int main() {
    freopen("fwt.in","r",stdin);
    freopen("fwt.out","w",stdout);
    n = read(); m = read(); k = read();
    fac[0]=fac[1]=inv[0]=inv[1]=invf[0]=invf[1]=1;
    for(int i = 2;i <= n;i ++) {
        fac[i] = fac[i-1] *1ll* i % MOD;
        inv[i] = (MOD - inv[MOD%i]) *1ll* (MOD/i) % MOD;
        invf[i] = invf[i-1] *1ll* inv[i] % MOD;
    }
    for(int i = 1;i <= n;i ++) {
        s = read(); a[s] ++;
    }
    FWTXOR(a,k);
    dp[0] = (m&1) ? (MOD-C(n,m)):C(n,m);
    // cerr<<"OK"<<endl;
    A[0] = 1;
    solve(1,n,0);
    // for(int i = 1;i <= n;i ++) printf("%d ",dp[i]); ENDL;
    for(int i = 0;i < k;i ++) {
        if(a[i] > n) a[i] -= MOD;
        int ti = (a[i]+n)>>1;
        a[i] = dp[ti];
    }
    IFWTXOR(a,k);
    for(int i = 0;i < k;i ++) AIput(a[i],i==k-1 ? '\n':' ');
	return 0;
}