学习构造哈夫曼树，这一篇足矣

1.哈夫曼树

HC=((d,0),(i,10),(a,110),(n,111))

2.如何构造哈夫曼树

构造哈夫曼树非常简单，将所有的节点放到一个队列中，用一个节点替换两个频率最低的节点，新节点的频率就是这两个节点的频率之和。这样，新节点就是两个被替换节点的父节点了。如此循环，直到队列中只剩一个节点(树根)。

1. 对给定的n个权值{W1,W2,W3,…,Wi,…,Wn}构成n棵二叉树的初始集合F= {T1,T2,T3,…,Ti,…,Tn}，其中每棵二叉树Ti中只有一个权值为Wi的根结点，它的左右子树均为空。

2. 在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，新二叉树的根结点的权值为其左右子树的根结点的权值之和。

3. 从F中删除这两棵树，并把这棵新的二叉树同样以升序排列加入到集合F中。

4. 重复二和三两步，直到集合F中只有一棵二叉树为止。

举个例子：

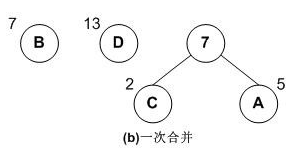
• 如图有A，B，C，D共4棵二叉树，其权值分别为5，7，2，13
  

1. 选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，即A和C，新二叉树的根结点的权值为其左右子树的根结点的权值之和，即2+5=7
   
2. 继续在此基础上，选择一棵根节点结点权值小的树作为新构造的二叉树的左子树，即B和7，新二叉树的根结点的权值为其左右子树的根结点的权值之和，即7+7=14
   
3. 继续在此基础上，选择一棵根节点结点权值小的树作为新构造的二叉树的左子树，即D和14，新二叉树的根结点的权值为其左右子树的根结点的权值之和，即13+14=27
   
4. 此时哈夫曼树构成
5. 引入二进制编码，各叶子结点的二进制编码如下：D(0),B(10),C(110),(111)

编程题：
1.领会哈夫曼的构造过程以及哈夫曼编码的生产过程
2.构造一棵哈夫曼树，输出对应的哈夫曼编码和平均查找长度

#include <stdio.h>
#include <string.h>
#define N 50 
#define M 2 * N-1 

typedef struct
{
	char data[5]; 
	int weight; 
	int parent; 
	int lchild; 
	int rchild; 
}HTNode;

typedef struct
{
	char cd[N]; 
	int start; 
}HCode;

void CreateHT(HTNode ht[],int n) 
{
	int i,k,lnode,rnode;
	int min1,min2;
	for (i=0;i<2*n-1;i++) 
		ht[i].parent=ht[i].lchild=ht[i].rchild=-1;
	for (i=n;i<2*n-1;i++) 
	{
		min1=min2=32767; 
		lnode = rnode = -1;
		for(k=0;k<=i-1;k++) 
		if(ht[k].parent==-1) 
		{
		if(ht[k].weight<min1)
			{
				min2=min1;
				rnode=lnode;
				min1=ht[k].weight;
				lnode=k;
			}
		else if(ht[k].weight<min2)
			{
				min2=ht[k].weight;
				rnode=k;
			}
		}
	ht[lnode].parent=i;
	ht[rnode].parent=i;
	ht[i].weight=ht[lnode].weight+ht[rnode].weight;
	ht[i].lchild=lnode;
	ht[i].rchild=rnode;
	}
}

void CreateHCode(HTNode ht[],HCode hcd[],int n) 
{
	int i,f,c;
	HCode hc;
	for(i=0;i<n;i++) 
	{
		hc.start=n;
		c=i;
		f=ht[i].parent; 
		while(f!=-1)
		{
			if(ht[f].lchild==c) 
				hc.cd[hc.start--]='0';
			else 
				hc.cd[hc.start--]='1';
			c=f;
			f=ht[f].parent;
		}
		hc.start++; 
		hcd[i]=hc;
	}
}

void DispHCode(HTNode ht[],HCode hcd[],int n) 
{
	int i,k; 
	int sum=0,m=0,j;
	printf("输出哈夫曼编码:\n");
	for (i=0;i<n;i++)
	{
		j=0;
		printf("	%s:\t",ht[i].data);
		for(k=hcd[i].start;k<=n;k++)
		{
			printf("%c",hcd[i].cd[k]);
			j++;
		}
		m+=ht[i].weight;
		sum+=ht[i].weight * j;
		printf("\n");
	}
	printf("\n平均长度=%g\n",1.0 * sum/m);
}

int main()
{
	int n=15,i;
	char * str[]={"The","of","a","to","and","in","that","he","is","at","on","for","His","are","be"};
	int fnum[]={1192,677,541,518,462,450,242,195,190,181,174,157,138,124,123};
	HTNode ht[M];
	HCode hcd[N];
	for(i=0;i<n;i++)
	{
		strcpy(ht[i].data,str[i]);
		ht[i].weight=fnum[i];
	}
	CreateHT(ht,n);
	CreateHCode(ht,hcd,n);
	DispHCode(ht,hcd,n);
	return 1;
}