matlab实现数值积分 【二】（integral函数）

如果被积函数的数学表达式已知，但解析解不易求，可使用数值积分的方法求解积分。

函数调用格式

应用举例

例1：求解数值解并检验其精度

计算积分$$f(x)=\frac{2}{\sqrt{\pi }}{\int }_0^{1.5}{e}^{-t^2}\mathrm{d}t$$

f = @(x) 2/sqrt(pi)*exp(-x.^2);  % //匿名函数
y = integral(f,0,1.5)  % //数值求解

结果为 $y=$0.96610514647531

求解解析解：
syms x, y0=vpa(int(2/sqrt(pi)*exp(-x^2),0,1.5),60)
结果为：$y_0=$0.96610514647531

结论：可以看出，默认选项下数值解函数integral()便可保证高精度的数值解。

例2：分段函数积分

给定如下分段函数：
$$f(x)=\{\begin{array}{ll}{e}^{x^2},& 0\le x\le 2\\ \frac{80}{4-\sin (16\pi x)},& 2<x\le 4\end{array}$$
计算积分值$I={\int }_0^{4}f(x)\mathrm{d}x$。

• 绘制$f(x)$填充图

x=[0:0.01:2, 2+eps:0.01:4,4]; 
y=exp(x.^2).*(x<=2)+80./(4-sin(16*pi*x)).*(x>2); 
x=[eps,x,4-eps]; y=[0,y,0]; fill(x,y,'g') %//绘制填充图

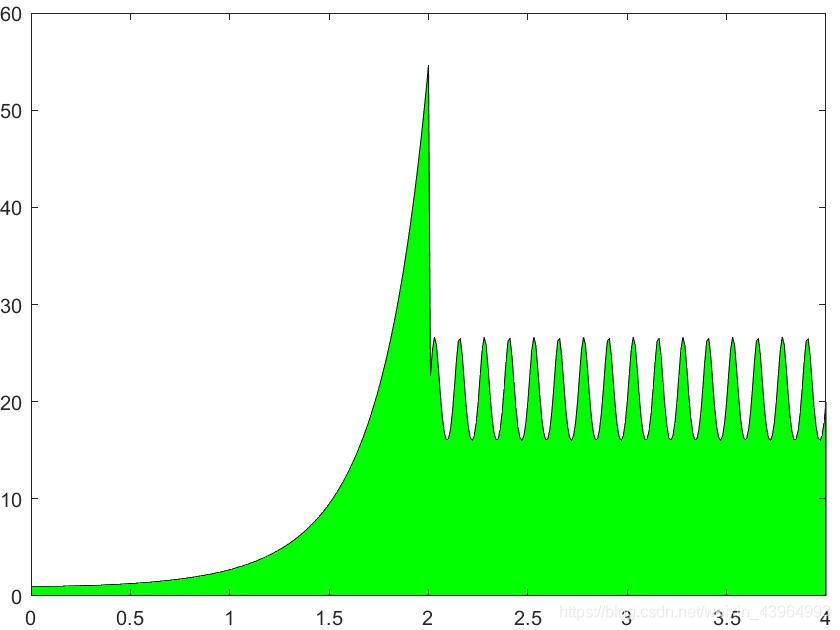
• 求解与验证

f = @(x) exp(x.^2).*(x<=2)+80./(4-sin(16*pi*x)).*(x>2); 
I1 = integral(f,0,4)   %//数值解
I2 = integral(f,0,4,'RelTol',1e-20)   %//提高精度
syms x
f = piecewise( x<=2, exp(x^2),  x>2, 80/(4-sin(16*pi*x)) ); 
I0 = vpa(int(f,x,0,4))   %//解析解

结果为：

变量	值
$I_0$（精确解析解）	57.76445012505301 033331523538518
$I_1$（正常数值解）	57.7644501250 4850495815844624303
$I_2$（高精度数值解）	57.76445012505301 690453052287921

例3：与梯形法比较

重新计算积分
$${\int }_0^{\frac{3\pi }{2}}\cos (15x)\mathrm{d}x$$

• 梯形法求解链接
• 数值求解：

f = @(x) cos(15*x); 
S=integral(f,0,3*pi/2,'RelTol',1e-20)

结论：和梯形法相比，速度和精度明显提高。

例4：大范围积分

计算积分$${\int }_0^{100}\cos (15x)\mathrm{d}x$$

f = @(x)cos(15*x); 
I1 = integral(f,0,100,'RelTol',1e-20)  %//数值解
syms x 
I0 = int(cos(15*x),x,0,100); vpa(I0)   %//解析解

解析解：$I_0=-0.066260130460443564274928241303306$
数值解：$I_1=-0.066260130460282923303694246897066$

例5：广义积分的数值计算

计算$${\int }_0^{\infty }{e}^{-x^2}\mathrm{d}x$$

f = @(x) exp(-x.^2); 
I1 = integral(f,0,inf,'RelTol',1e-20)  %//数值解
syms x
I0 = int(exp(-x^2),0,inf); vpa(I0)     %//解析解

解析解：$I_0=0.88622692545275801364908374167057$
数值解：$I_1=0.88622692545275805198201624079957$

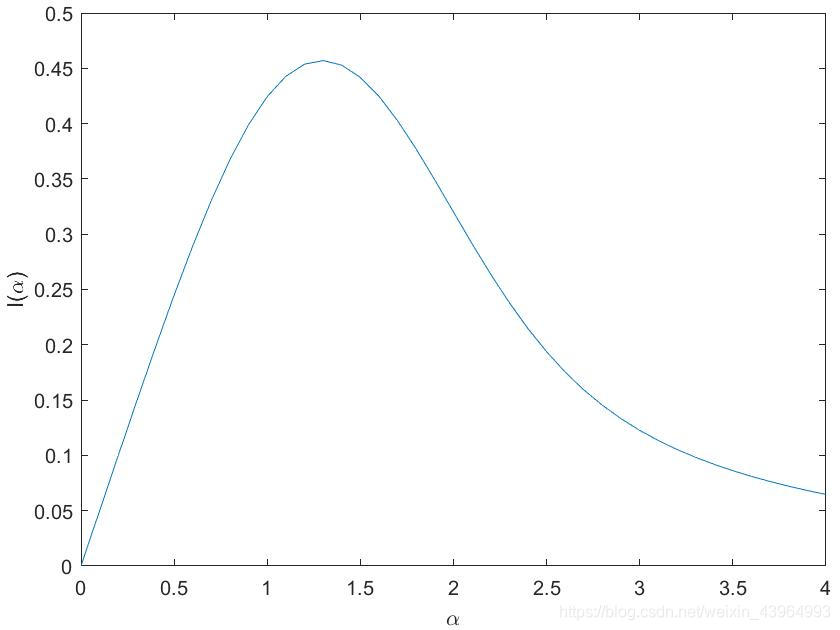
例6：含参函数数值积分

绘制积分函数$I(\alpha )$曲线$$I(\alpha )={\int }_0^{\infty }{e}^{-\alpha x^2}\sin (\alpha x^2)\mathrm{d}x$$

a = 0:0.1:4;
f = @(x)exp(-a*x.^2).*sin(a.^2*x);
I = integral(f,0,inf,'RelTol',1e-20,'ArrayValued',true);
plot(a,I),  xlabel('\alpha'),  ylabel('I(\alpha)')