[AcWing]849. Dijkstra求最短路 I（C++实现）朴素Dijkstra算法求最短路模板题

最新推荐文章于 2024-03-06 23:57:54 发布

原创

最新推荐文章于 2024-03-06 23:57:54 发布 · 1.2k 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #c语言

本文详细解析了朴素Dijkstra算法的原理，展示了如何用C++解决849题最短路径问题。通过实例演示了图的初始化、距离更新和关键步骤，并介绍了所需前置知识和数据结构。重点在于理解算法思想和循环次数的确定。

[AcWing]849. Dijkstra求最短路 I（C++实现）朴素Dijkstra算法求最短路模板题

1. 题目
2. 读题（需要重点注意的东西）
3. 解法
4. 可能有帮助的前置习题
5. 所用到的数据结构与算法思想
6. 总结

1. 题目

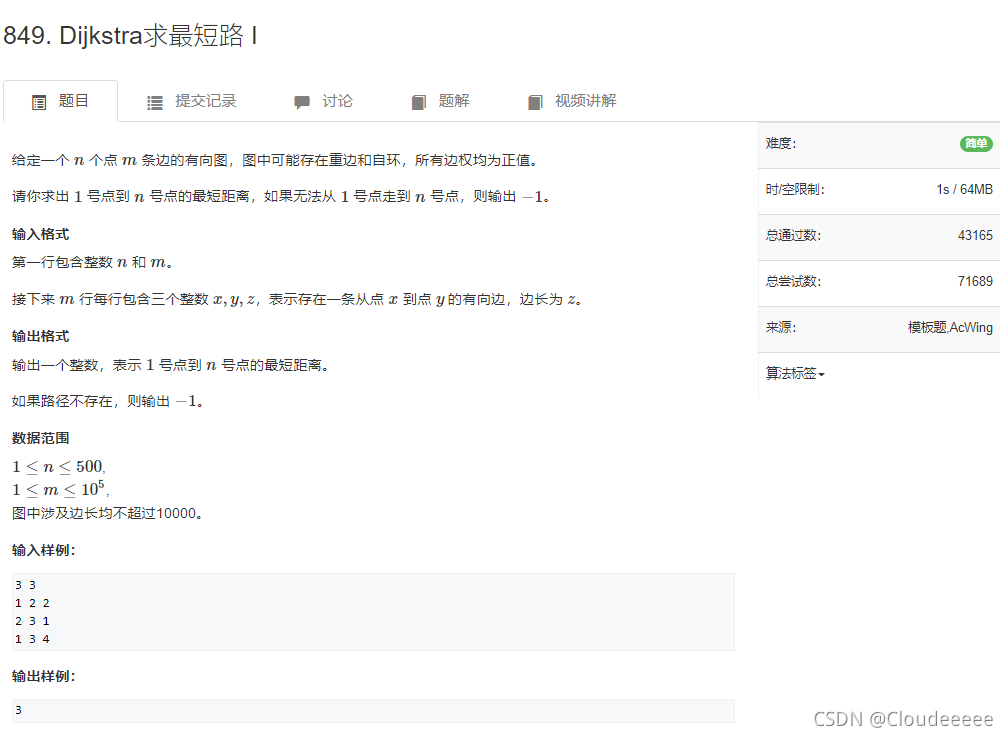
在这里插入图片描述

2. 读题（需要重点注意的东西）

思路：朴素Dijkstraa算法的主要思想如图
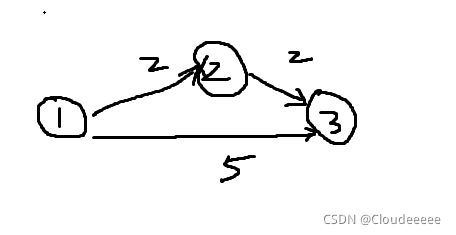
在这里插入图片描述

d[i]表示第i个节点到第一个节点的距离
首先将d[1]置位0，d[1] = 0；

然后用节点1更新与之相连的所有节点的距离：
d[2] = 2;
d[3] = 5;

然后找到剩余节点中离节点1距离最小的节点为节点2；

然后再用节点2更新与之相连的节点的距离：
d[3] = d[2] + 2 = 4（节点2到节点3的距离）
因为此时 d[2] + 2 < d[3] ，所以更新 d[3] = 4;

这个更新操作，就称之为Dijkstra算法。（3个节点，总共需要更新2次；那么n个节点，总共需要更新n-1次）

3. 解法

---------------------------------------------------解法---------------------------------------------------

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510;

int n, m;
int g[N][N]; // 图g，存的是两条边之间的距离，如g[a][b]存的就是a到b的距离
int dist[N]; // 从1号点走到每个点的最短距离是多少
bool st[N]; // i号点的距离是否确定了

int dijkstra()
{
   
          
    // 将所有的距离初始化为无穷
    memset(dist,