本笔记摘自知乎博主旺财的搬砖历险记和叶强,仅用于自学
0.数学规范
- 大写字母表示随机变量: S , A , R S,A,R S,A,R等
- 小写字母表示具体的值: s , a , r s,a,r s,a,r等
- 空心字母表示统计运算符: E , P \mathbb{E},\mathbb{P} E,P等
- 花体字母表示集合或函数: S , A , P \mathcal{S},\mathcal{A},\mathcal{P} S,A,P等
1.马尔科夫过程
(1)MDPs的介绍
- 在强化学习中,MDP对完全可观测的环境进行描述
- 即观察到的状态内容完整的决定了决策需要的特征
- 几乎所有强化学习的问题都可以转化为MDP
- 最优控制问题 ⟷ \longleftrightarrow ⟷连续MDPs
- 部分观测环境的问题 ⟷ \longleftrightarrow ⟷POMDPs
- 赌博机问题 ⟷ \longleftrightarrow ⟷只有一个状态的MDPs
(2)马尔科夫性
“The future is independent of the past given the present”
当且仅当 t t t时刻的状态 S t S_t St满足 P [ S t + 1 ∣ S t ] = P [ S t + 1 ∣ S 1 , S 2 , … , S t ] \mathbb{P}[S_{t+1}\vert S_t]=\mathbb{P}[S_{t+1}\vert S_1,S_2,\ldots, S_t] P[St+1∣St]=P[St+1∣S1,S2,…,St]时,这个状态才称为马尔科夫状态,即该状态满足马尔科夫性
- 状态包含了所有的历史相关信息
- 一旦状态 S t S_t St已知,则历史信息 S 1 , S 2 , … , S t − 1 ] S_1,S_2,\ldots, S_{t-1}] S1,S2,…,St−1]可以抛弃
- 状态是将来的充分统计量。因此这里要求环境全观测。
(3)状态转移矩阵
- 状态转移概率
- 指从一个马尔科夫状态 s s s跳转到后继状态 s ′ s^{\prime} s′的状态转移的概率: P S S ′ = P [ S t + 1 = s ′ ∣ S t = s ] \mathcal{P} _{SS^{\prime}}=\mathbb{P}[S_{t+1}=s^{\prime}\vert S_t=s] PSS′=P[St+1=s′∣St=s]
- 状态转移矩阵
- 定义了从所有状态
s
s
s跳转到所有后继状态
s
′
s^{\prime}
s′的概率
- 当状态数量无穷大(连续状态)时,更适合使用状态转移函数: ∫ S ′ P ( s ′ ∣ s ) = 1 \int_{S^{\prime}}\mathcal{P}(s^{\prime}\vert s)=1 ∫S′P(s′∣s)=1
- n n n为状态数量,矩阵中每一行元素和为1: ∑ S ′ P ( s ′ ∣ s ) = 1 \sum_{S^{\prime}}\mathcal{P}(s^{\prime}\vert s)=1 ∑S′P(s′∣s)=1
- 定义了从所有状态
s
s
s跳转到所有后继状态
s
′
s^{\prime}
s′的概率
P = [ P 11 … P 1 n ⋮ ⋮ P n 1 … P n n ] \mathcal{P}=\begin{bmatrix} P_{11} & \dots & P_{1n}\\ \vdots & & \vdots\\ P_{n1} &\dots & P_{nn} \end{bmatrix} P=⎣⎢⎡P11⋮Pn1……P1n⋮Pnn⎦⎥⎤
(4)片段episode
在RL中,从初始状态 S 1 S_1 S1到终止状态 S T S_T ST的一个序列过程被称为一个episode: S 1 , S 2 , … , S T S_1,S_2,\ldots,S_T S1,S2,…,ST
- 如果一个任务总以终止状态结束,这个任务称为片段任务episodic task
- 如果一个任务没有终止状态, 无限执行,称为连续性任务continuing task
(5)马尔科夫过程
又叫马尔科夫链(Markov Chain),是一个无记忆的随机过程,可以用一个元组 ⟨ S , P ⟩ \langle{\mathcal{S}},{\mathcal{P}}\rangle ⟨S,P⟩表示。
⭐ S \mathcal{S} S是有限数量的状态集合
⭐ P \mathcal{P} P是状态转移矩阵 P S S ′ = P [ S t + 1 = s ′ ∣ S t = s ] \mathcal{P}_{SS^{\prime}}=\mathbb{P}[S_{t+1}=s^{\prime}\vert S_t=s] PSS′=P[St+1=s′∣St=s]
马尔科夫链其实是状态空间为可数集的马尔科夫过程。
💗注意💗:
- 一般情况下我们不知道 P \mathcal{P} P的具体值,但通常假设 P \mathcal{P} P是稳定存在的
- 当 P \mathcal{P} P不稳定时,就是不稳定环境,需要在线学习
一个 n n n阶马尔科夫过程是状态间的转移仅依赖于前n个状态的过程。
2.马尔科夫奖励过程MRPs
(1)定义
马尔科夫奖励过程是带有values的马尔科夫链
马尔科夫奖励过程是是一个元组 ⟨ S , P , R , γ ⟩ \langle{\mathcal{S}},\mathcal{P}, {\mathcal{R}},{\mathcal{\gamma}}\rangle ⟨S,P,R,γ⟩
⭐ S \mathcal{S} S是有限状态集合
⭐ P \mathcal{P} P是状态转移矩阵 P S S ′ = P [ S t + 1 = s ′ ∣ S t = s ] \mathcal{P}_{SS^{\prime}}=\mathbb{P}[S_{t+1}=s^{\prime}\vert S_t=s] PSS′=P[St+1=s′∣St=s]
⭐ R \mathcal{R} R是奖励函数, R s = E [ R t + 1 ∣ S t = s ] \mathcal{R}_s=\mathbb{E}[R_{t+1}\vert S_t=s] Rs=E[Rt+1∣St=s],描述了在状态 s s s的标量奖励( R t + 1 R_{t+1} Rt+1是具体的奖励值, R s \mathcal{R}_s Rs是函数)
⭐ γ \gamma γ是折扣因子/衰减系数
(2)回报Return
回报 G t G_t Gt是从时刻 t t t开始所有的折扣奖励:
连续性任务: G t = R t + 1 + γ R t + 2 + … = ∑ k = 0 ∞ γ k R t + k + 1 G_t=R_{t+1}+\gamma R_{t+2}+\ldots=\sum_{k=0}^\infty\gamma ^kR_{t+k+1} Gt=Rt+1+γRt+2+…=∑k=0∞γkRt+k+1
片段性任务: G t = R t + 1 + γ R t + 2 + … + γ T − t − 1 R T = ∑ k = 0 T − t − 1 γ k R t + k + 1 G_t=R_{t+1}+\gamma R_{t+2}+\ldots+\gamma^{T-t-1}R_T=\sum_{k=0}^{T-t-1}\gamma ^kR_{t+k+1} Gt=Rt+1+γRt+2+…+γT−t−1RT=∑k=0T−t−1γkRt+k+1
⭐ γ ∈ [ 0 , 1 ] \gamma \in [0,1] γ∈[0,1],代表未来回报对于现在的价值
⭐奖励 R R R在第 k + 1 k+1 k+1步后为 γ k R \gamma^kR γkR
⭐即时奖励高于延迟奖励。 γ \gamma γ趋于0表示更青睐眼前利益, γ \gamma γ趋于1表示更有远见
✅如果将终止状态的自身转移概率为1、奖励为0,则连续性任务也可以表示成 G t = ∑ k = 0 T − t − 1 γ k R t + k + 1 G_t=\sum_{k=0}^{T-t-1}\gamma ^kR_{t+k+1} Gt=∑k=0T−t−1γkRt+k+1
💗注意💗:奖励是针对状态的,回报是针对片段的
🍄大部分马尔科夫奖励和决策过程都是折扣的:
- 从数学上讲很方便
- 避免陷入循环马尔科夫过程的无限奖励
- 未来的回报有一定的不确定性
- 如果奖励是经济学上的,即时奖励会比延迟奖励获得更多利益
- 动物/人类的行为表现出对即时奖励的偏爱
- 有时也用未折扣的马尔科夫奖励过程( γ = 1 \gamma=1 γ=1),如果所有的序列都终止
(3)价值函数
值函数 v ( s ) v(s) v(s)给出了状态 s s s的长期回报。
状态价值函数 v ( s ) v(s) v(s)是从状态 s s s开始的期望回报: v ( s ) = E [ G t ∣ S t = s ] v(s)=\mathbb{E}[G_t\vert S_t=s] v(s)=E[Gt∣St=s]
(4)马尔可夫奖励过程的贝尔曼方程
价值函数可以被分解为两部分: v ( s ) = E [ R t + 1 + γ v ( S t + 1 ) ∣ S t = s ] v(s)=\mathbb{E}[R_{t+1}+\gamma v(S_{t+1})\vert S_t=s] v(s)=E[Rt+1+γv(St+1)∣St=s]
- 立即回报 R t + 1 R_{t+1} Rt+1
- 后续状态的折扣函数
γ
v
(
S
t
+
1
)
\gamma v(S_{t+1})
γv(St+1)
💡证明: v ( s ) = E [ G t ∣ S t = s ] = E [ R t + 1 + γ G t + 1 ∣ S t = s ] = E [ R t + 1 + γ v ( S t + 1 ) ∣ S t = s ] v(s) = \mathbb{E}[G_t\vert S_t=s] = \mathbb{E}[R_{t+1}+\gamma G_{t+1}\vert S_t=s] = \mathbb{E}[R_{t+1}+\gamma v(S_{t+1})\vert S_t=s] v(s)=E[Gt∣St=s]=E[Rt+1+γGt+1∣St=s]=E[Rt+1+γv(St+1)∣St=s]
💗注意💗: - 对 R t + 1 R_{t+1} Rt+1和 G t + 1 G_{t+1} Gt+1求期望,和的期望等于期望的和
- 这里用大写的 S t + 1 S_{t+1} St+1因为 S t = s S_t=s St=s的下一个状态是随机的
则贝尔曼方程:
v
(
s
)
=
R
s
+
γ
∑
s
′
∈
S
P
S
S
′
v
(
s
′
)
v(s)=R_s+\gamma \sum_{s^{\prime}\in \mathcal{S}}\mathcal{P}_{SS^{\prime}}v(s^{\prime})
v(s)=Rs+γs′∈S∑PSS′v(s′)
💡证明:
v
(
s
)
=
E
[
R
t
+
1
+
γ
v
(
S
t
+
1
)
∣
S
t
=
s
]
=
E
[
R
t
+
1
∣
S
t
=
s
]
+
E
[
γ
v
(
S
t
+
1
)
∣
S
t
=
s
]
=
R
s
+
γ
∑
s
′
∈
S
P
S
S
′
v
(
s
′
)
v(s) = \mathbb{E}[R_{t+1}+\gamma v(S_{t+1})\vert S_t=s] = \mathbb{E}[R_{t+1}\vert S_t=s] + \mathbb{E}[\gamma v(S_{t+1})\vert S_t=s] = R_s+\gamma \sum_{s^{\prime}\in \mathcal{S}}\mathcal{P}_{SS^{\prime}}v(s^{\prime})
v(s)=E[Rt+1+γv(St+1)∣St=s]=E[Rt+1∣St=s]+E[γv(St+1)∣St=s]=Rs+γs′∈S∑PSS′v(s′)
💗注意💗:
- 已知状态转移矩阵 P \mathcal{P} P
- 随机变量求期望参考下面的定义
对于大范围的MRPs,有许多迭代理论来计算状态价值函数,如动态规划、蒙特卡洛估计、时间差分学习
数学期望:
离散型的随机变量 X X X有概率函数 P ( X = x k ) = P k ( k = 1 , 2 , … ) P(X=x_k)=P_k(k=1,2,\ldots) P(X=xk)=Pk(k=1,2,…),若级数 ∑ k = 1 ∞ x k p k \sum_{k=1}^\infty x_kp_k ∑k=1∞xkpk绝对收敛,则称这个级数为 X X X的数学期望
(5)贝尔曼方程的矩阵形式和求解
1)矩阵形式
贝尔曼方程可以写成如下的矩阵形式:
v
=
R
+
γ
P
v
v=\mathcal{R}+\gamma \mathcal{P}v
v=R+γPv
其中,
v
v
v是一个列向量,每个状态只有一个分量。
假设状态集合
S
=
{
s
1
,
s
2
,
…
,
s
n
}
\mathcal{S}=\{s_1,s_2,\ldots,s_n\}
S={s1,s2,…,sn},则贝尔曼方程可以展开写成:
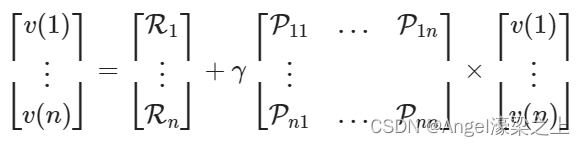
2)求解
贝尔曼方程本质是一个线性方程,可以直接解:
(
1
−
γ
P
)
v
=
R
,
v
=
(
1
−
γ
P
)
−
1
R
(1-\gamma \mathcal{P})v =\mathcal{R},v= (1-\gamma \mathcal{P})^{-1}\mathcal{R}
(1−γP)v=R,v=(1−γP)−1R
💗注意💗:
- 这里的1是单位矩阵
3.马尔科夫决策过程MDPs
(1)定义
马尔可夫决策过程是带有决策的马尔科夫奖励过程
马尔科夫决策过程是是一个元组 ⟨ S , A , P , R , γ ⟩ \langle{\mathcal{S}},\mathcal{A}, \mathcal{P}, {\mathcal{R}},{\mathcal{\gamma}}\rangle ⟨S,A,P,R,γ⟩
⭐ S \mathcal{S} S是有限状态集合
⭐ A \mathcal{A} A是有限动作集合
⭐ P \mathcal{P} P是状态转移矩阵, P S S ′ a = P [ S t + 1 = s ′ ∣ S t = s , A t = a ] \mathcal{P}_{SS^{\prime}}^a=\mathbb{P}[S_{t+1}=s^{\prime}\vert S_t=s,A_t=a] PSS′a=P[St+1=s′∣St=s,At=a]
⭐ R \mathcal{R} R是奖励函数, R s a = E [ R t + 1 ∣ S t = s , A t = a ] \mathcal{R}_s^a=\mathbb{E}[R_{t+1}\vert S_t=s,A_t=a] Rsa=E[Rt+1∣St=s,At=a],描述了在状态 s s s的标量奖励( R t + 1 R_{t+1} Rt+1是具体的奖励值, R s \mathcal{R}_s Rs是函数)
⭐ γ \gamma γ是折扣因子/衰减系数
💗注意💗:
这里的
P
\mathcal{P}
P和
R
\mathcal{R}
R和具体的行为
a
a
a对应,而马尔科夫奖励过程的
P
\mathcal{P}
P和
R
\mathcal{R}
R只与状态有关
(2)策略
策略 π \pi π是给定状态的行为概率分布: π ( a ∣ s ) = P [ A t = a ∣ S t = s ] \pi(a\vert s)=\mathbb{P}[A_t=a\vert S_t=s] π(a∣s)=P[At=a∣St=s]
- 一个策略完全定义了agent的行为方式,包含agent在各个状态下的各种可能的行为方式及其概率大小
- MDP的策略仅和当前状态有关,与历史信息无关
- 策略是静态的,与时间无关,但agent可以随着时间更新策略 A t ∼ π ( ⋅ ∣ S t ) , f o r a l l t > 0 A_t\sim \pi(\cdot \vert S_t),for \ all \ t > 0 At∼π(⋅∣St),for all t>0
- 如果策略的概率分布输出是one-hot的,则该策略为确定性策略;否则该策略为随机策略
one-hot:
一个向量里,只有一个元素为1,其余均为0
💡给定一个MDP M = ⟨ S , A , P , R , γ ⟩ \mathcal{M}=\langle{\mathcal{S}},\mathcal{A}, \mathcal{P}, {\mathcal{R}},{\mathcal{\gamma}}\rangle M=⟨S,A,P,R,γ⟩和一个策略 π \pi π,那么:
- 状态序列 S 1 , S 2 , … S_1,S_2,\ldots S1,S2,…是一个马尔科夫过程 ⟨ S , P π ⟩ \langle{\mathcal{S}}, \mathcal{P}^\pi\rangle ⟨S,Pπ⟩
- 状态和奖励序列
S
1
,
R
1
,
S
2
,
R
2
,
…
S_1,R_1,S_2,R_2,\ldots
S1,R1,S2,R2,…是一个马尔科夫奖励过程
⟨
S
,
P
π
,
R
π
,
γ
⟩
\langle{\mathcal{S}}, \mathcal{P}^\pi, \mathcal{R}^\pi,\gamma\rangle
⟨S,Pπ,Rπ,γ⟩
- 在执行策略 π \pi π时,状态从 s s s转移到 s ′ s^{\prime} s′的概率等于一系列概率的和,这一系列概率指在执行当前策略时,执行某一行为的概率×该行为能使得状态从 s s s转移到 s ′ s^{\prime} s′的概率: P S , S ′ π = ∑ a ∈ A π ( a ∣ s ) P S S ′ a \mathcal{P}^\pi_{S,S^{\prime}}=\sum \limits_{a\in\mathcal{A}}\pi(a\vert s)\mathcal{P}^a_{SS^{\prime}} PS,S′π=a∈A∑π(a∣s)PSS′a
- 在执行策略
π
\pi
π时,得到的即时奖励是,该策略下执行所有可能行为得到的奖励×该行为的概率:
R
S
π
=
∑
a
∈
A
π
(
a
∣
s
)
R
S
a
\mathcal{R}^\pi_{S}=\sum \limits_{a\in\mathcal{A}}\pi(a\vert s)\mathcal{R}^a_{S}
RSπ=a∈A∑π(a∣s)RSa
🎀补充说明
- 策略在MDP中的作用:相当于agent可以在某一个状态做出选择,从而有形成各种马尔科夫过程的可能
- 基于策略产生的每一个马尔科夫过程是一个马尔科夫奖励过程,各过程之间的差别是不同选择产生了不同的后续状态、对应不同的奖励
(3)基于策略 π \pi π的价值函数
状态价值函数 v π ( s ) v_\pi(s) vπ(s)是MDP下基于策略 π \pi π从状态 s s s获得的期望回报,衡量agent在状态 s s s时的价值大小 v π ( s ) = E [ G t ∣ S t = s ] v_\pi(s)=\mathbb{E}[G_t\vert S_t=s] vπ(s)=E[Gt∣St=s]
动作价值函数 q π ( s , a ) q_\pi(s,a) qπ(s,a)是MDP下基于策略 π \pi π选择动作 a a a后,从状态 s s s获得的期望回报,衡量状态 s s s时执行动作 a a a的价值大小 q π ( s , a ) = E [ G t ∣ S t = s , A t = a ] q_\pi(s,a)=\mathbb{E}[G_t\vert S_t=s,A_t=a] qπ(s,a)=E[Gt∣St=s,At=a]
💗注意💗:
- 策略是静态的,不随状态改变而改变
- 变化的是,在某一个状态时,根据策略可能产生的具体行为,因为具体行为有一定概率
- 策略就是用来描述各个不同状态下执行各个不同行为的概率
- 行为价值函数一般是与某一特定的状态相对应的,即状态行为对价值函数。
(4)Bellman期望方程(Bellman Expectation Equation)
1)状态-价值与行为-价值函数
状态-价值函数可以继续分解为即时奖励➕后续状态的折扣价值:
v
π
(
s
)
=
E
[
R
t
+
1
+
γ
v
π
(
S
t
+
1
)
∣
S
t
=
s
]
v_\pi(s)=\mathbb{E}[R_{t+1}+\gamma v_\pi(S_{t+1})\vert S_t=s]
vπ(s)=E[Rt+1+γvπ(St+1)∣St=s]
行为-价值函数也可以同样分解:
q
π
(
s
,
a
)
=
E
[
R
t
+
1
+
γ
q
π
(
S
t
+
1
,
A
t
+
1
)
∣
S
t
=
s
,
A
t
=
a
]
q_\pi(s,a)=\mathbb{E}[R_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1})\vert S_t=s,A_t=a]
qπ(s,a)=E[Rt+1+γqπ(St+1,At+1)∣St=s,At=a]
2)价值函数分解
在遵循策略
π
\pi
π时,状态
s
s
s的价值体现为在该状态下采取可能行为的价值与发生概率的求和:
v
π
(
s
)
=
∑
a
∈
A
π
(
a
∣
s
)
q
π
(
s
,
a
)
v_\pi(s)=\sum_{a\in\mathcal{A}}\pi(a\vert s)q_\pi(s,a)
vπ(s)=a∈A∑π(a∣s)qπ(s,a)
类似的,行为-价值函数也可以分成离开这个状态的价值➕所有进入新的状态的价值与其转移概率成绩的和,表示成:
q
π
(
s
,
a
)
=
R
s
a
+
γ
∑
s
′
∈
S
P
S
S
′
a
v
π
(
s
′
)
q_\pi(s,a)=\mathcal{R}_s^a+\gamma \sum_{s^{\prime}\in S}\mathcal{P}_{SS^{\prime}}^av_\pi(s^{\prime})
qπ(s,a)=Rsa+γs′∈S∑PSS′avπ(s′)
3)价值函数重组
组合起来可以得到:
v
π
(
s
)
=
∑
a
∈
A
π
(
a
∣
s
)
q
π
(
s
,
a
)
=
∑
a
∈
A
π
(
a
∣
s
)
(
R
s
a
+
γ
∑
s
∈
S
′
P
S
S
′
a
v
π
(
s
′
)
)
v_\pi(s)=\sum_{a\in\mathcal{A}}\pi(a\vert s)q_\pi(s,a)=\sum_{a\in\mathcal{A}}\pi(a\vert s)(\mathcal{R}_s^a+\gamma \sum_{s\in S^{\prime}}\mathcal{P}_{SS^{\prime}}^av_\pi(s^{\prime}))
vπ(s)=a∈A∑π(a∣s)qπ(s,a)=a∈A∑π(a∣s)(Rsa+γs∈S′∑PSS′avπ(s′))
本质上等价于
v
π
(
s
)
=
E
[
R
t
+
1
+
γ
v
π
(
S
t
+
1
)
∣
S
t
=
s
]
v_\pi(s)=\mathbb{E}[R_{t+1}+\gamma v_\pi(S_{t+1})\vert S_t=s]
vπ(s)=E[Rt+1+γvπ(St+1)∣St=s]
将
v
π
(
s
′
)
v_\pi(s^{\prime})
vπ(s′)继续拆开:
q
π
(
s
,
a
)
=
R
s
a
+
γ
∑
s
∈
S
′
P
S
S
′
a
v
π
(
s
′
)
=
R
s
a
+
γ
∑
s
∈
S
′
P
S
S
′
a
∑
a
′
∈
A
π
(
a
′
∣
s
′
)
q
π
(
s
′
,
a
′
)
q_\pi(s,a)=\mathcal{R}_s^a+\gamma \sum_{s\in S^{\prime}}\mathcal{P}_{SS^{\prime}}^av_\pi(s^{\prime})=\mathcal{R}_s^a+\gamma \sum_{s\in S^{\prime}}\mathcal{P}_{SS^{\prime}}^a\sum_ {a^{\prime}\in\mathcal{A}}\pi(a^{\prime}\vert s^{\prime})q_\pi(s^{\prime},a^{\prime})
qπ(s,a)=Rsa+γs∈S′∑PSS′avπ(s′)=Rsa+γs∈S′∑PSS′aa′∈A∑π(a′∣s′)qπ(s′,a′)
本质上等价于
q
π
(
s
,
a
)
=
E
[
R
t
+
1
+
γ
q
π
(
S
t
+
1
,
A
t
+
1
)
∣
S
t
=
s
,
A
t
=
a
]
q_\pi(s,a)=\mathbb{E}[R_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1})\vert S_t=s,A_t=a]
qπ(s,a)=E[Rt+1+γqπ(St+1,At+1)∣St=s,At=a]
(5)Bellman期望方程矩阵形式
Bellman期望方程可以用MRP简明地表示
v
π
=
R
π
+
γ
P
π
v
π
v_\pi=\mathcal{R}^{\pi}+\gamma \mathcal{P^{\pi}}v_\pi
vπ=Rπ+γPπvπ
则解得
v
π
=
(
1
−
γ
P
π
)
−
1
R
π
v_\pi=(1-\gamma \mathcal{P^{\pi}})^{-1}\mathcal{R}^{\pi}
vπ=(1−γPπ)−1Rπ
(6)最优价值函数
最优状态价值函数 v ∗ ( s ) v_*(s) v∗(s)是所有策略产生的状态价值函数中,最大的状态价值: v ∗ ( s ) = max π v π ( s ) v_*(s)=\max \limits_\pi v_\pi(s) v∗(s)=πmaxvπ(s) 最优动作价值函数 q ∗ ( s , a ) q_*(s,a) q∗(s,a)是从所有策略产生的动作价值函数中,最大的动作价值: q ∗ ( s , a ) = max π q π ( s , a ) q_*(s,a)=\max \limits_\pi q_\pi(s,a) q∗(s,a)=πmaxqπ(s,a)
- 最优价值函数明确了MDP的最优可能表现
- 当我们知道了最优价值函数,也就知道了每个状态的最优价值,MDP就已经解决了
(7)最优策略
对于任何状态 s s s,遵循策略 π \pi π的价值不小于遵循策略 π ′ \pi^{\prime} π′的价值,则策略 π \pi π优于 π ′ \pi^{\prime} π′: π ≥ π ′ i f v π ( s ) ≥ v π ′ ( s ) , ∀ s \pi\geq \pi^{\prime} \ if\ v_\pi(s) \geq v_{\pi^{\prime}}(s),\forall s π≥π′ if vπ(s)≥vπ′(s),∀s
对于任意MDP,有:
⭐存在一个最优策略,比其他策略更好至少相等 π ∗ ≥ π , ∀ π \pi_*\geq\pi,\forall \pi π∗≥π,∀π
⭐所有的最优策略都有相同的最优价值函数 v π ∗ ( s ) = v ∗ ( s ) v_{\pi_*}(s)=v_*(s) vπ∗(s)=v∗(s)
⭐所有的最优策略都有相同的最优动作价值函数 q π ∗ ( s , a ) = q ∗ ( s , a ) q_{\pi_*}(s,a)=q_*(s,a) qπ∗(s,a)=q∗(s,a)
❗寻找最优策略
可以通过最大化最优动作价值函数
q
∗
(
s
,
a
)
q_*(s,a)
q∗(s,a)来寻找最优策略
对于任何MDP问题,总存在一个确定性的最优策略
如果我们直到最有动作价值函数
q
∗
(
s
,
a
)
q_*(s,a)
q∗(s,a),我们就找到了最优策略
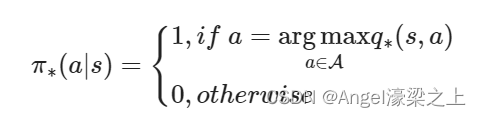
(8)Bellman最优方程
1)最优状态价值函数
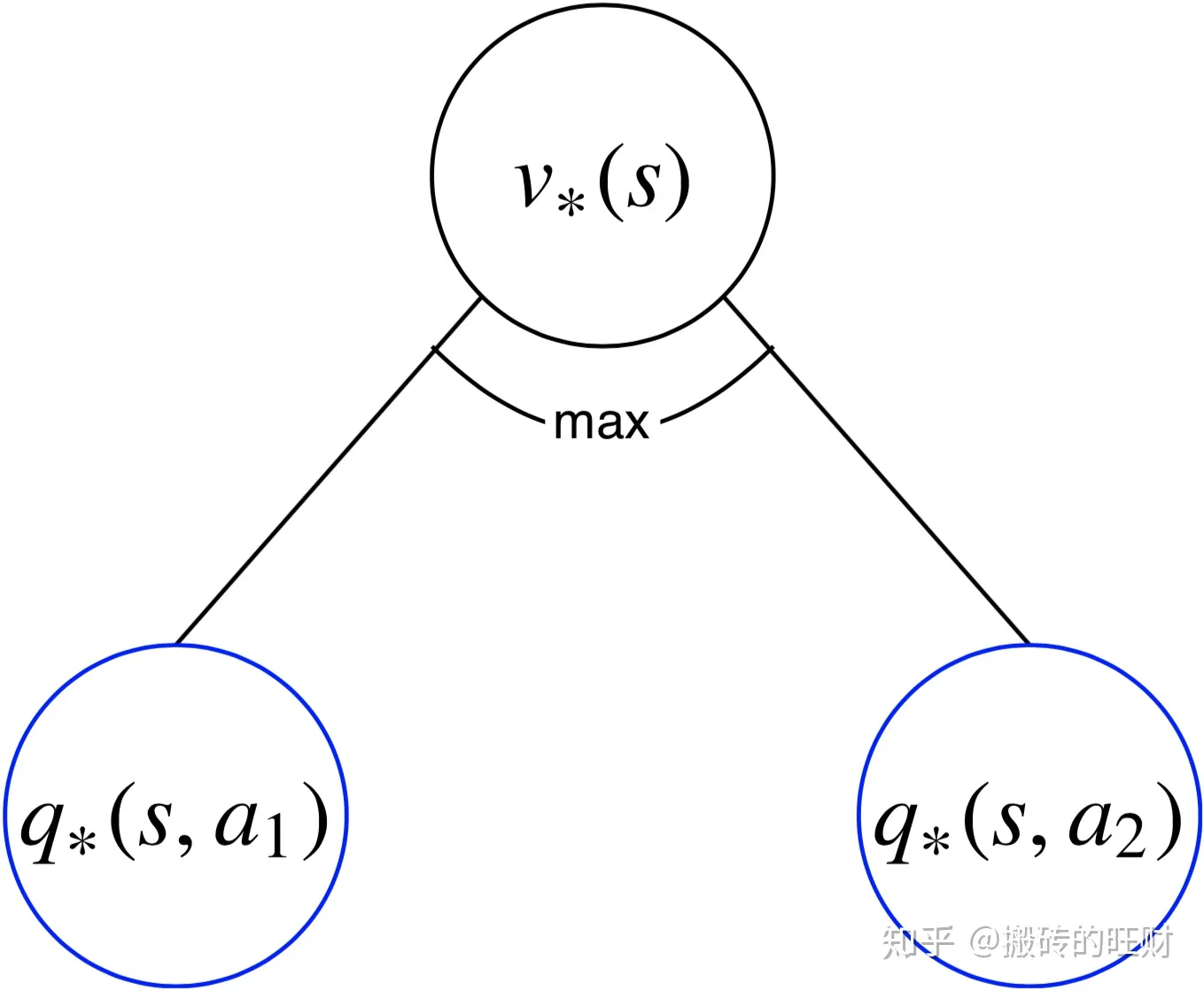
一个状态的最优价值(最优状态价值),等于从该状态出发,采取的所有动作的动作价值中最大的一个的动作价值:
v
∗
(
s
)
=
max
a
q
∗
(
s
,
a
)
v_*(s)=\max_aq_*(s,a)
v∗(s)=amaxq∗(s,a)
由下式可知
v
π
(
s
)
=
∑
a
∈
A
π
(
a
∣
s
)
q
π
(
s
,
a
)
v_\pi(s)=\sum_ {a\in\mathcal{A}}\pi(a\vert s)q_\pi(s,a)
vπ(s)=a∈A∑π(a∣s)qπ(s,a)
假设最优策略是确定性的策略,则
π
∗
(
s
,
a
)
{\pi_*}(s,a)
π∗(s,a)是one-hot的形式,只需取最大的
q
π
∗
(
s
,
a
)
q_{\pi_*}(s,a)
qπ∗(s,a),且所有的最优策略有相同的动作价值函数,即
q
π
∗
(
s
,
a
)
=
q
∗
(
s
,
a
)
q_{\pi_*}(s,a)=q_*(s,a)
qπ∗(s,a)=q∗(s,a):
v
∗
(
s
)
=
v
π
∗
(
s
)
=
∑
a
∈
A
π
∗
(
a
∣
s
)
q
π
∗
(
s
,
a
)
=
max
a
q
π
∗
(
s
,
a
)
=
max
a
q
∗
(
s
,
a
)
v_*(s)=v_{\pi_*}(s)=\sum_ {a\in\mathcal{A}}{\pi_*}(a\vert s)q_{\pi_*}(s,a)=\max _aq_{\pi_*}(s,a)=\max \limits_aq_*(s,a)
v∗(s)=vπ∗(s)=a∈A∑π∗(a∣s)qπ∗(s,a)=amaxqπ∗(s,a)=amaxq∗(s,a)
2)最优价值函数拆解
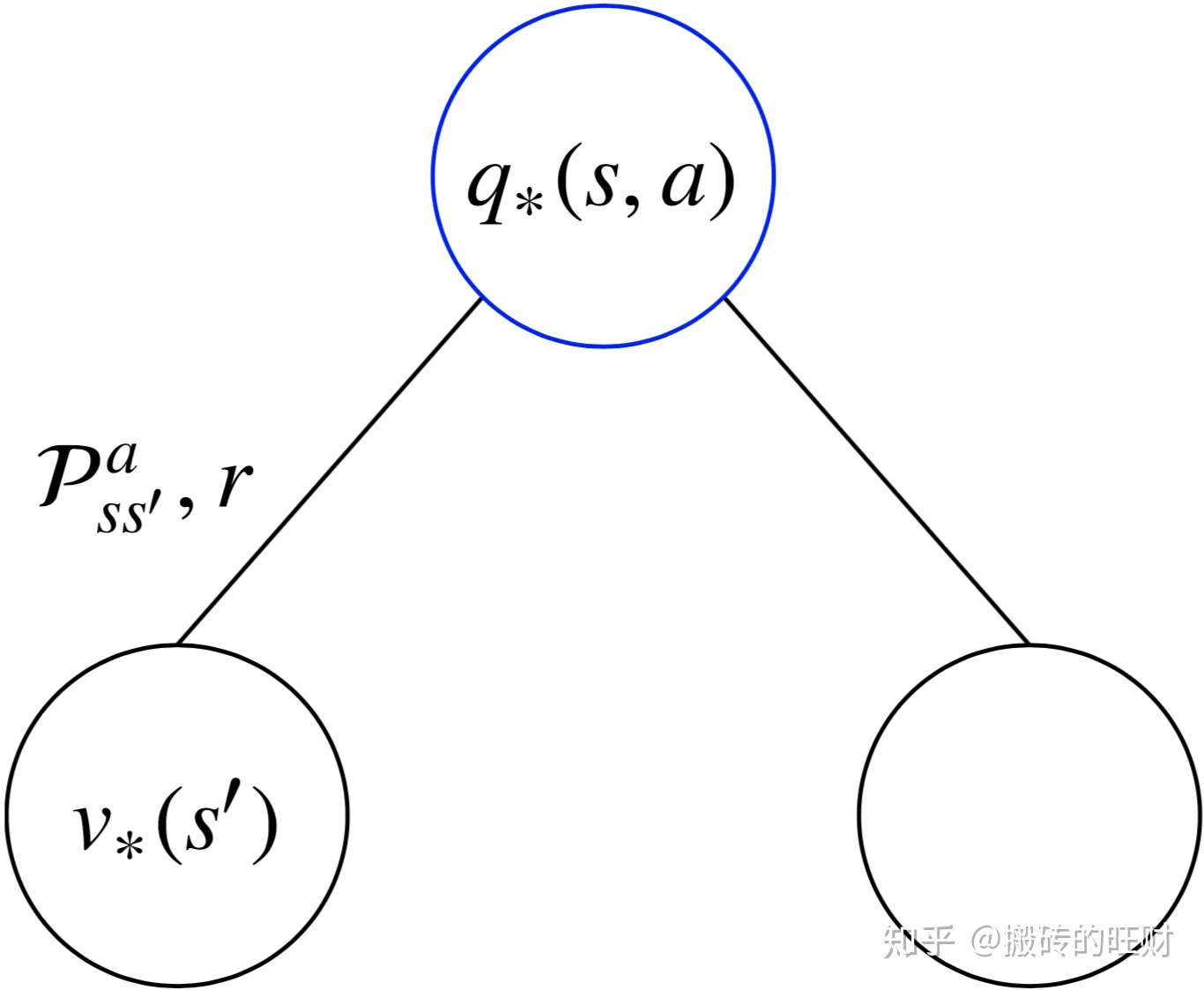
在某个状态下,采取某个行为的最优价值=离开该状态的即时奖励➕所有能到达的新的状态的最优价值按出现概率求和:
q
∗
(
s
,
a
)
=
R
s
a
+
γ
∑
s
′
∈
S
P
S
S
′
a
v
∗
(
s
′
)
q_*(s,a)=\mathcal{R}_s^a+\gamma \sum \limits_{s^{\prime}\in \mathcal{S}}\mathcal{P}_{SS^{\prime}}^av_*(s^{\prime})
q∗(s,a)=Rsa+γs′∈S∑PSS′av∗(s′)
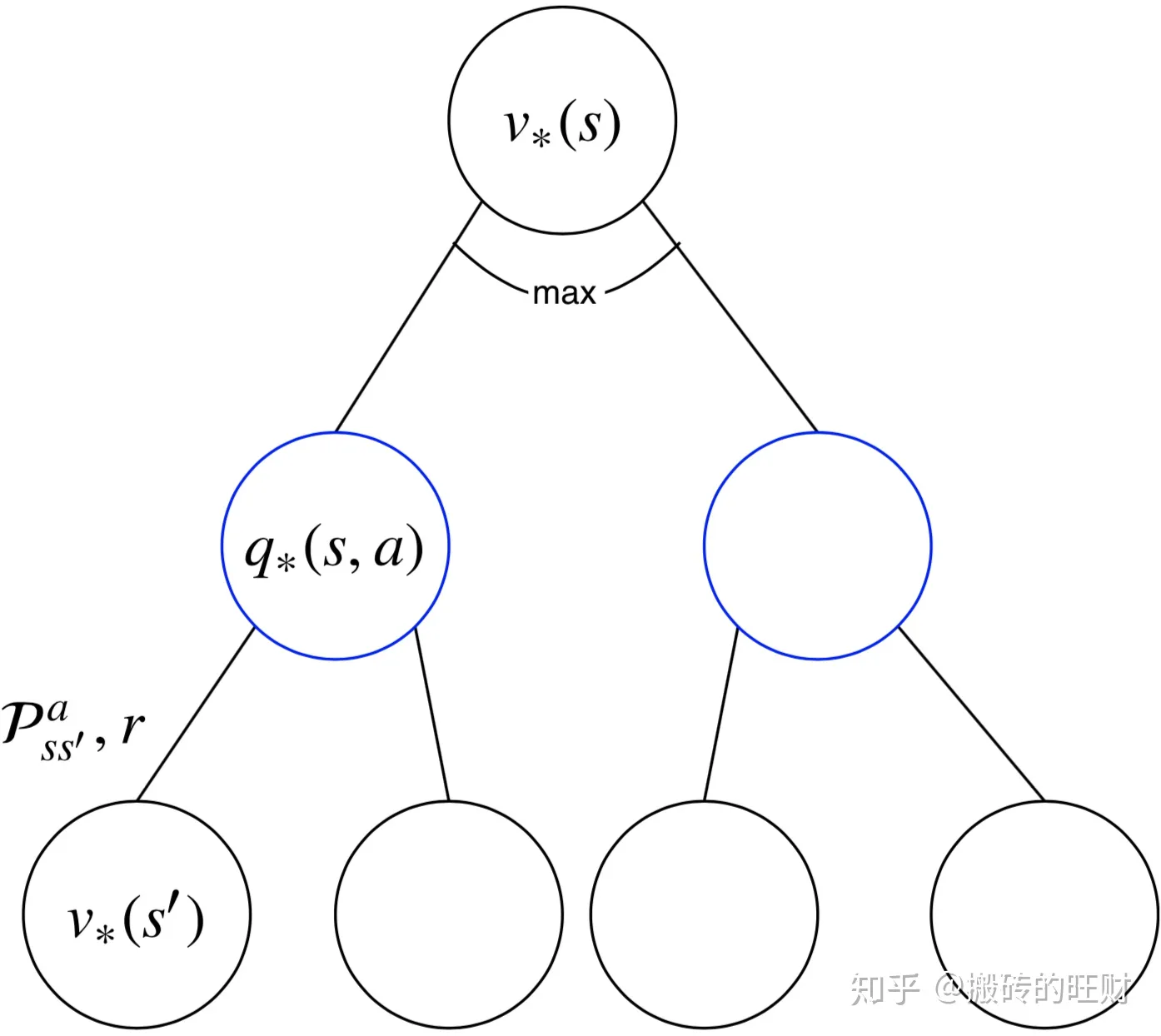
与
v
∗
(
s
)
=
max
a
q
∗
(
s
,
a
)
v_*(s)=\max \limits_aq_*(s,a)
v∗(s)=amaxq∗(s,a)组合起来,有:
v
∗
(
s
)
=
max
a
(
R
s
a
+
γ
∑
s
′
∈
S
P
S
S
′
a
v
∗
(
s
′
)
)
v_*(s)=\max \limits_a(\mathcal{R}_s^a+\gamma \sum \limits_{s^{\prime}\in \mathcal{S}}\mathcal{P}_{SS^{\prime}}^av_*(s^{\prime}))
v∗(s)=amax(Rsa+γs′∈S∑PSS′av∗(s′))
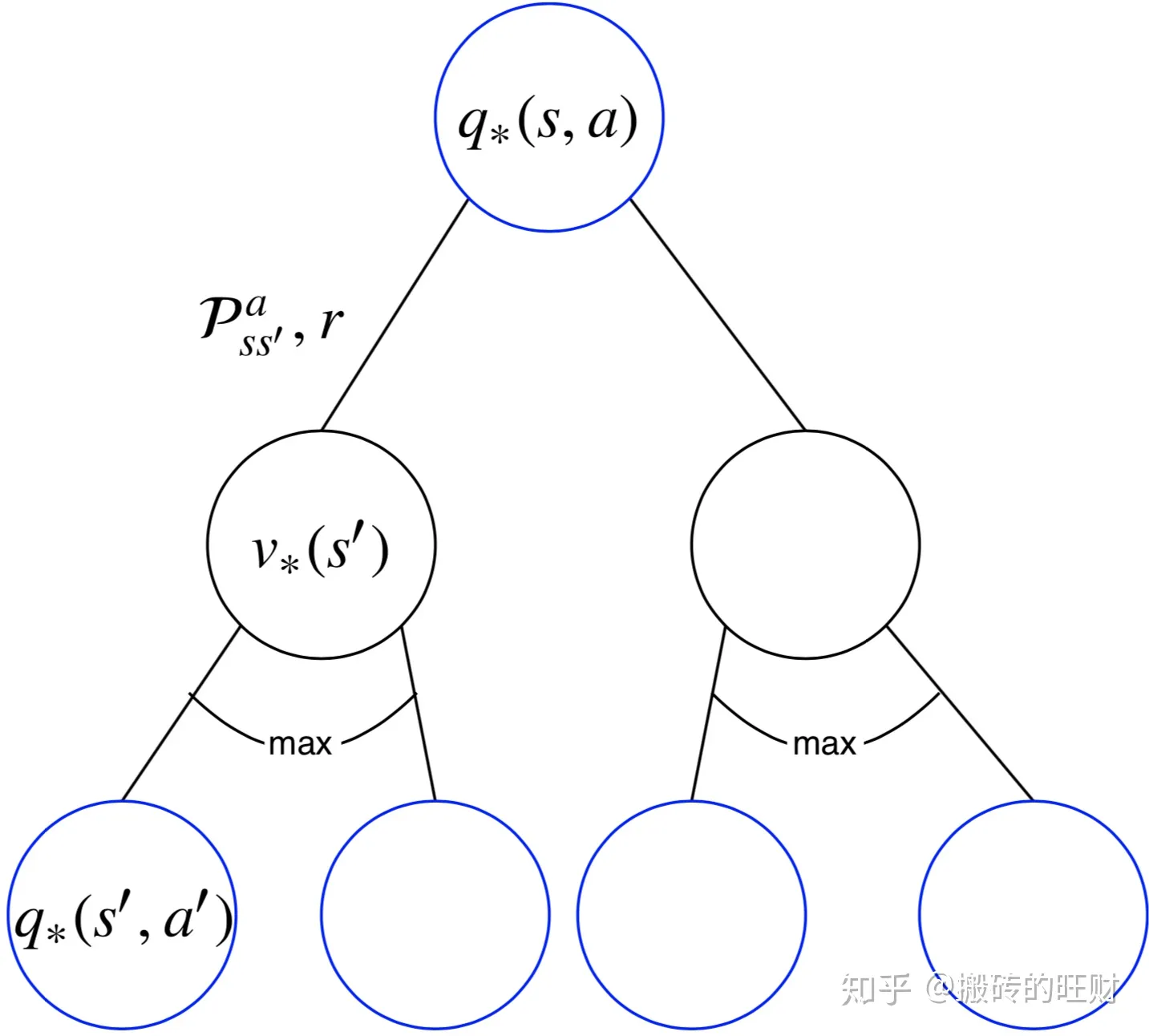
针对
q
∗
(
s
,
a
)
q_*(s,a)
q∗(s,a),有:
q
∗
(
s
,
a
)
=
R
s
a
+
γ
∑
s
′
∈
S
P
S
S
′
a
max
a
q
∗
(
s
′
,
a
′
)
q_*(s,a)=\mathcal{R}_s^a+\gamma \sum \limits_{s^{\prime}\in \mathcal{S}}\mathcal{P}_{SS^{\prime}}^a\max \limits_aq_*(s^{\prime},a^{\prime})
q∗(s,a)=Rsa+γs′∈S∑PSS′aamaxq∗(s′,a′)
3)贝尔曼最优方程和贝尔曼方程的关系
- 贝尔曼最优方程利用了 π ∗ \pi_* π∗的特点,将求期望的算子转化成了 m a x a max_a maxa
- 在贝尔曼期望方程中, π \pi π是已知的,但是在贝尔曼最优方程中, π ∗ \pi_* π∗未知
- 解贝尔曼期望的方程对应了评价,解贝尔曼最优方程的过程对应了优化
4)贝尔曼最优方程求解
- Bellman最优方程是非线性的
- 没有固定的解决方案
- 有很多迭代方法可以解决:
- 值迭代
- 策略迭代
- Q-learning
- Sarsa
4.MDP扩展
(1)无穷和连续MDPs
考虑到动作空间或状态空间的连续性,MDP有几下几种扩展:
- 动作空间或状态空间的大小为无穷可数
- 直接求取
- 动作空间或状态空无限不可数(连续)
- 在线性最小二乘(LQR)模式中有闭式解
- 时间连续(参考《Adaptive optimal control for continuous-time linear systems based on policy iteration》)
- 需要偏微分方程
- HJB方程(Hamilton-Jacobi-Bellman)
- Bellman方程在时间步长趋近于0的极限情况
(2)部分可观测的MDPs(POMDPs)
对于复杂的系统来说,难以获得系统的精确状态,POMDPs是更接近真实世界的模型。
部分可观察马尔可夫决策过程是一种具有隐藏状态的MDP。它是一个带有动作的隐马尔可夫模型。
除了前提是部分可观测外,POMDPs也基于MDP类似的假设,采用最大化期望奖励的方法
一个POMDP是一个元组 ⟨ S , A , O , P , R , Z , γ ⟩ \langle{\mathcal{S}},\mathcal{A}, \mathcal{O},\mathcal{P}, {\mathcal{R}},\mathcal{Z},{\mathcal{\gamma}}\rangle ⟨S,A,O,P,R,Z,γ⟩
⭐ S \mathcal{S} S是有限状态集合
⭐ A \mathcal{A} A是有限动作集合
⭐ O \mathcal{O} O是有限的观测集合
⭐ P \mathcal{P} P是状态转移矩阵, P S S ′ a = P [ S t + 1 = s ′ ∣ S t = s , A t = a ] \mathcal{P}_{SS^{\prime}}^a=\mathbb{P}[S_{t+1}=s^{\prime}\vert S_t=s,A_t=a] PSS′a=P[St+1=s′∣St=s,At=a]
⭐ R \mathcal{R} R是奖励函数, R s a = E [ R t + 1 ∣ S t = s , A t = a ] \mathcal{R}_s^a=\mathbb{E}[R_{t+1}\vert S_t=s,A_t=a] Rsa=E[Rt+1∣St=s,At=a],描述了在状态 s s s的标量奖励( R t + 1 R_{t+1} Rt+1是具体的奖励值, R s \mathcal{R}_s Rs是函数)
⭐ Z \mathcal{Z} Z是观察函数,表明状态和观察值之间的关系 Z S ′ o a = P [ O t + 1 = o ∣ S t + 1 = s ′ , A t = a ] \mathcal{Z}_{S^{\prime}o}^a=\mathbb{P}[O_{t+1}=o\vert S_{t+1}=s^{\prime},A_t=a] ZS′oa=P[Ot+1=o∣St+1=s′,At=a]
⭐ γ \gamma γ是折扣因子/衰减系数
在POMDP中,agent不能确定自己处于哪个状态,因此对于下一步动作的选择的决策基础是当前所处状态的概率(最有可能处于哪个状态)。因此,agent需要通过传感器收集环境信息,来更新对自己当前所处状态的可信度。这里不是直接把agent导向目标点,而是选择一个缓冲一般让agent先运动到邻近位置,在这个邻近位置收集到的环境信息加大了对自己所处状态的可信度。在确信自己所处的状态后,agent做出的动作决策才是更有效的。
历史 H t H_t Ht是 t t t时刻观察、动作和奖励的序列: H t = A 0 , O 1 , R 1 , … , A t − 1 , O t , R t H_t=A_0,O_1,R_1,\ldots,A_{t-1},O_t,R_t Ht=A0,O1,R1,…,At−1,Ot,Rt
这种存储方式会消耗大量存储空间,可以采用较短的历史代替所有的观察和行为。Astrom提出用状态上的概率,引入信念状态 b ( h ) b(h) b(h)的概念,来表示agent对自己所处状态的可信度。
一个信念状态 b ( h ) b(h) b(h)是一个状态的概率分布,以历史h为条件: b ( h ) = ( P [ S t = s 1 ∣ H t = h ] , … , P [ S t = s n ∣ H t = h ] ) b(h)=(\mathbb{P}[S_t=s^1\vert H_t=h],\ldots,\mathbb{P}[S_t=s^n\vert H_t=h]) b(h)=(P[St=s1∣Ht=h],…,P[St=sn∣Ht=h])
信念状态 b ( h ) b(h) b(h)是对历史 H t H_t Ht的 充分估计,所有状态上维护一个概率分布可以与维护一个完整历史提供同样的信息。以前解决POMDP问题时,需要知道历史动作才能决定当前的操作,这种解决方案是非马尔科夫链。引入信念状态后,POMDP问题可以转化为基于信念空间的马尔科夫链来求解,即把POMDP问题转化为求解信念状态函数和策略的问题。
- 历史 H t H_t Ht满足Markov性质
- 信念状态
b
(
h
)
b(h)
b(h)也满足Markov性质
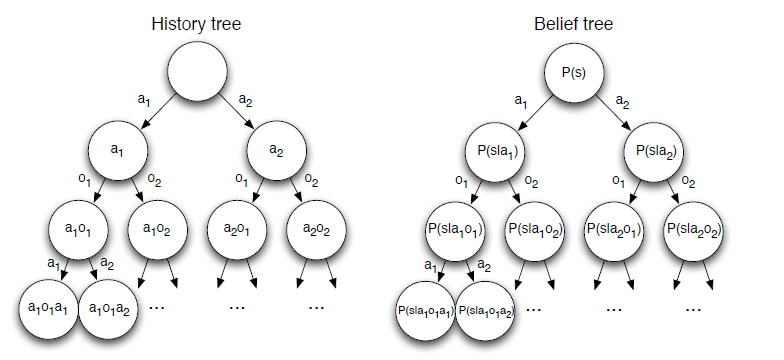
因此,一个POMDP可以简化为一个无限的历史树,从而简化为一个无限的信念状态树
(3)非折扣的、平均奖励的MDPs
1)遍历马尔科夫过程
马尔科夫链的遍历性可以理解为任意取一个时间段,所有状态都有出现的可能。遍历马尔可夫链是非周期的平稳的马尔科夫链,有长时间尺度下的稳定行为,是被广泛研究应用的马尔科夫链。遍历马尔可夫过程具有:
- 周期性:每个状态被访问无限次。
- 非周期性:每个状态被访问时没有任何系统周期
遍历马尔科夫过程有以下性质的极限平稳分布 d π ( s ) d^\pi(s) dπ(s): d π ( s ) = ∑ s ′ d π ( s ′ ) P S ′ S d^\pi(s)=\sum \limits _{s^\prime}d^\pi(s^\prime)\mathcal{P}_{S^\prime S} dπ(s)=s′∑dπ(s′)PS′S
如果任何策略引起的马尔科夫链都是遍历的,则MDP是遍历的。
对于任何策略
π
\pi
π,一个遍历MDP的每个时间步长
ρ
π
\rho^\pi
ρπ的平均奖励与开始状态无关
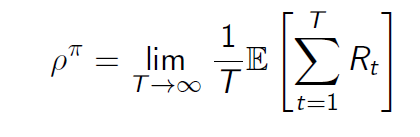
2)平均奖励的值函数
- 一个未折现的、遍历的MDP的价值函数可以用平均奖励表示。
- v ~ π ( s ) \tilde{v}_\pi(s) v~π(s)是从状态 s s s开始的额外奖励: v ~ π ( s ) = E π [ ∑ k = 1 ∞ ( R t + k − ρ π ) ∣ S t = s ] \tilde{v}_\pi(s)=\mathbb{E}_\pi[\sum_{k=1}^\infty(R_{t+k}-\rho^\pi)\vert S_t=s] v~π(s)=Eπ[k=1∑∞(Rt+k−ρπ)∣St=s]
- 有着相应的平均奖励贝尔曼方程: v ~ π ( s ) = E π [ ( R t + 1 − ρ π ) + ∑ k = 1 ∞ ( ( R t + k + 1 − ρ π ) ) ∣ S t = s ] = E π [ ( R t + 1 − ρ π ) + v ~ π ( S t + 1 ) ∣ S t = s ] \tilde{v}_\pi(s)=\mathbb{E}_\pi[(R_{t+1}-\rho^\pi)+\sum_{k=1}^\infty((R_{t+k+1}-\rho^\pi))\vert S_t=s] =\mathbb{E}_\pi[(R_{t+1}-\rho^\pi)+\tilde{v}_\pi(S_{t+1})\vert S_t=s] v~π(s)=Eπ[(Rt+1−ρπ)+k=1∑∞((Rt+k+1−ρπ))∣St=s]=Eπ[(Rt+1−ρπ)+v~π(St+1)∣St=s]
5.举例
(1)马尔科夫过程
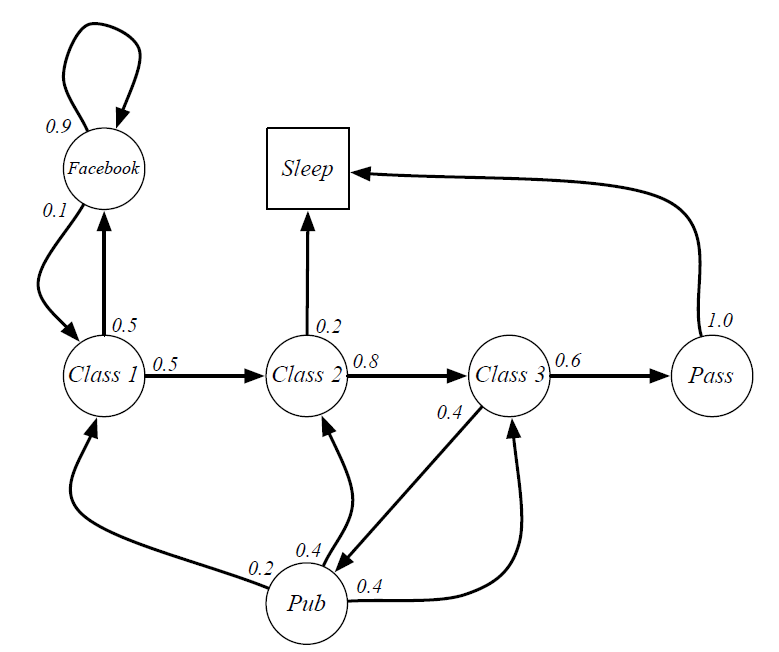
💡解释:
- 圆圈表示学生所处状态
- 方格Sleep为终止状态,或者可以描述为一个自循环的状态,即Sleep状态的下一个状态一定是自己
- 箭头上的数字表示当前转移的概率
💗注💗: - 终止状态的定义有两种,状态终止和时间终止
(2)状态转移矩阵

(3)马尔科夫奖励过程
1)图示
在马尔科夫过程的基础上增加了针对每个状态的奖励。(不包括衰减系数)
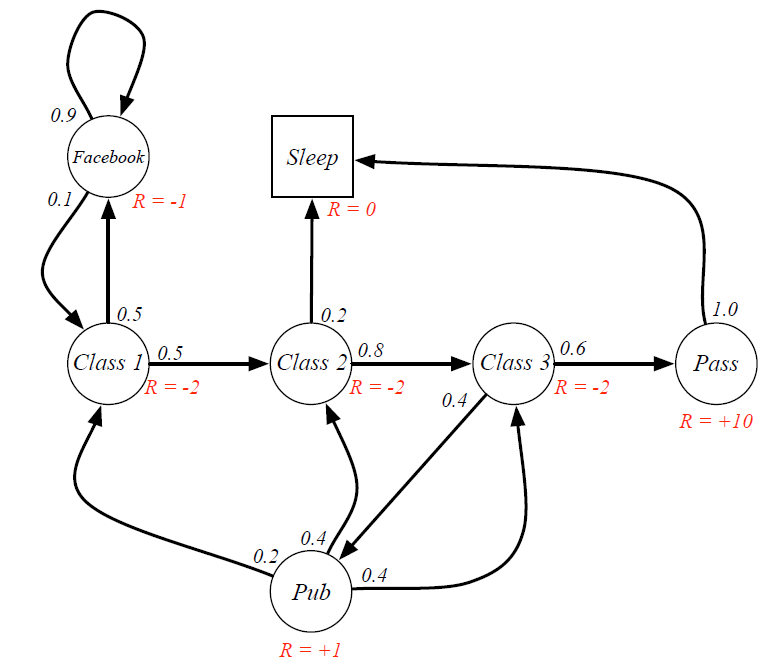
2)计算表:
第二行对应各状态的即时奖励值(该奖励只与状态本身有关,与从何而来无关);中间区域的数字为状态转移概率,即所在行状态转移到所在列状态的概率

3)计算示例
计算公式 G 1 = R 2 + γ R 3 + … + γ T − 2 R T G_1=R2+\gamma R_3+\ldots+\gamma^{T-2}R_T G1=R2+γR3+…+γT−2RT,这里 γ = 1 2 \gamma = \frac{1}{2} γ=21
- C1-FB-FB-C1-C2-Sleep v 1 = ( − 2 ) + ( − 1 ) × 1 2 + ( − 1 ) × ( 1 2 ) 2 + ( − 2 ) × ( 1 2 ) 3 + ( − 2 ) × ( 1 2 ) 4 + 0 = − 3.125 v_1=(-2)+(-1)\times\frac{1}{2}+(-1)\times(\frac{1}{2})^2+(-2)\times(\frac{1}{2})^3+(-2)\times(\frac{1}{2})^4+0=-3.125 v1=(−2)+(−1)×21+(−1)×(21)2+(−2)×(21)3+(−2)×(21)4+0=−3.125
- C1-C2-C3-Pass-Sleep
v
1
=
(
−
2
)
+
(
−
2
)
×
1
2
+
(
−
2
)
×
(
1
2
)
2
+
10
×
(
1
2
)
3
+
0
=
−
2.25
v_1=(-2)+(-2)\times\frac{1}{2}+(-2)\times(\frac{1}{2})^2+10\times(\frac{1}{2})^3+0=-2.25
v1=(−2)+(−2)×21+(−2)×(21)2+10×(21)3+0=−2.25
虽然都是从相同的初始状态开始,但是不同的episode有不同的回报值,值函数则是它们的期望值
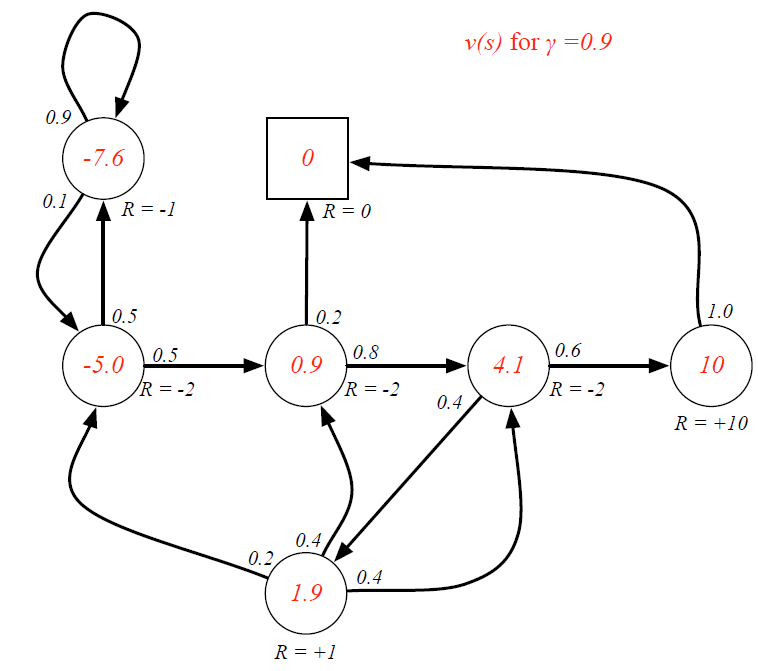
4) γ \gamma γ的影响
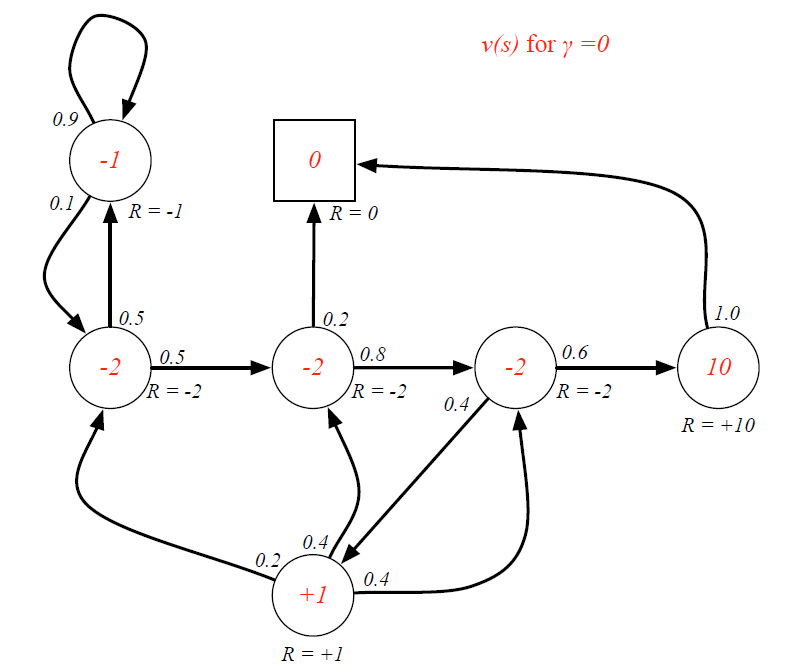
💗注💗:图中圆圈内的数字为该状态的价值,圈外的 R = − 2 R=-2 R=−2为该状态的即时奖励
-
γ
=
0
\gamma=0
γ=0时,各状态的价值与该状态的即时奖励相同
-
γ
≠
0
\gamma\neq0
γ=0时,各状态的价值需要计算得到
-
γ
=
0.9
\gamma=0.9
γ=0.9
-
γ
=
1
\gamma=1
γ=1
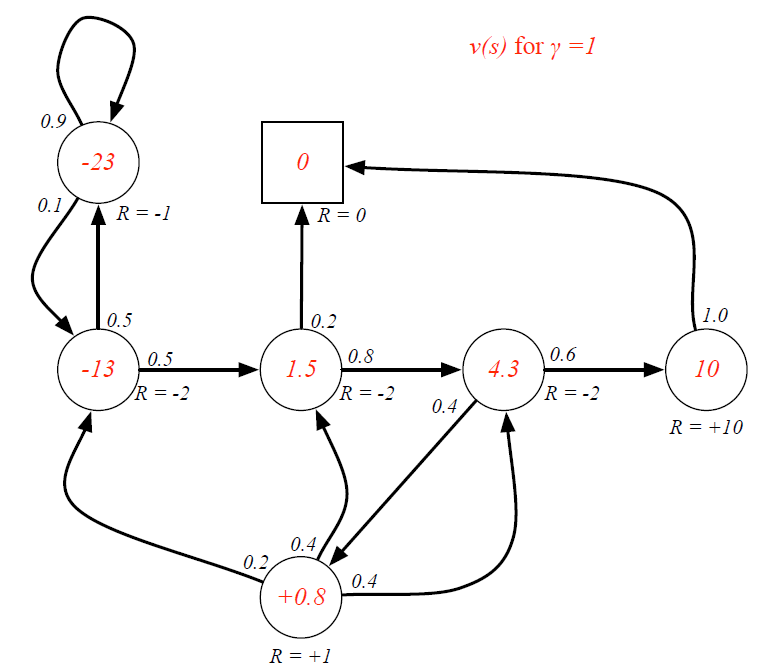 v
C
3
=
R
C
3
+
γ
P
C
3
P
a
s
s
×
v
p
a
s
s
+
(
P
C
3
P
u
b
×
v
P
u
b
)
=
−
2
+
1
×
(
0.6
×
10
+
0.4
×
0.8
)
=
4.3
v_{C3} =R_{C3}+ \gamma P_{C3Pass} \times v_{pass} + (P_{C3Pub} \times v_{Pub}) = -2+1\times (0.6\times 10+0.4 \times 0.8) = 4.3
vC3=RC3+γPC3Pass×vpass+(PC3Pub×vPub)=−2+1×(0.6×10+0.4×0.8)=4.3
v
C
3
=
R
C
3
+
γ
P
C
3
P
a
s
s
×
v
p
a
s
s
+
(
P
C
3
P
u
b
×
v
P
u
b
)
=
−
2
+
1
×
(
0.6
×
10
+
0.4
×
0.8
)
=
4.3
v_{C3} =R_{C3}+ \gamma P_{C3Pass} \times v_{pass} + (P_{C3Pub} \times v_{Pub}) = -2+1\times (0.6\times 10+0.4 \times 0.8) = 4.3
vC3=RC3+γPC3Pass×vpass+(PC3Pub×vPub)=−2+1×(0.6×10+0.4×0.8)=4.3
-
γ
=
0.9
\gamma=0.9
γ=0.9
(4)贝尔曼方程求解

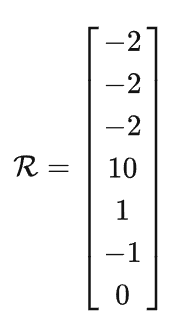
γ
=
1
\gamma = 1
γ=1
则

运用python求解
# coding:utf-8
import numpy as np
np.set_printoptions(precision=3, threshold=np.inf, linewidth=400, suppress=True)
gamma = 1.0
E = np.eye(7)
P = np.array([[0, 0.5, 0, 0, 0, 0.5, 0],
[0, 0, 0.8, 0, 0, 0, 0.2],
[0, 0, 0, 0.6, 0.4, 0, 0],
[0, 0, 0, 0, 0, 0, 1],
[0.2, 0.4, 0.4, 0, 0, 0, 0],
[0.1, 0, 0, 0, 0, 0.9, 0],
[0, 0, 0, 0, 0, 0, 1]])
R = np.array([-2, -2, -2, 10, 1, -1, 0]).T
# print(np.linalg.det(E-gamma*P))
# np.linalg.det(E-gamma*P) = 0.0 --> E-gamma*P是奇异矩阵
# 给矩阵主对角线每一个元素加一个很小的量,如1e-6,使其强制可逆
# print(np.linalg.det(E*1e-6 + E-gamma*P))
# np.linalg.det(E*1e-6 + E-gamma*P)=3.2401e-08
# print(np.linalg.inv(E*1e-6+E-gamma*P))
v = np.dot(np.linalg.inv(E*1e-6+E-gamma*P), R)
print("v={}".format(v))
# 输出 v=[-12.543 1.457 4.321 10. 0.803 -22.543 0. ]
❗❗❗问题:
- 使用这种求逆的计算复杂度是 O ( n 3 ) O(n^3) O(n3)
- 直接求解只适用于小规模的MRPs
- 大规模的MRPs的求解通常使用迭代法
- 动态规划(Dynamic Programming,DP)
- 蒙特卡洛评估(Monte-Carlo evaluation)
- 时序差分学习(Temporal-Difference,TD)
(5)马尔科夫决策过程
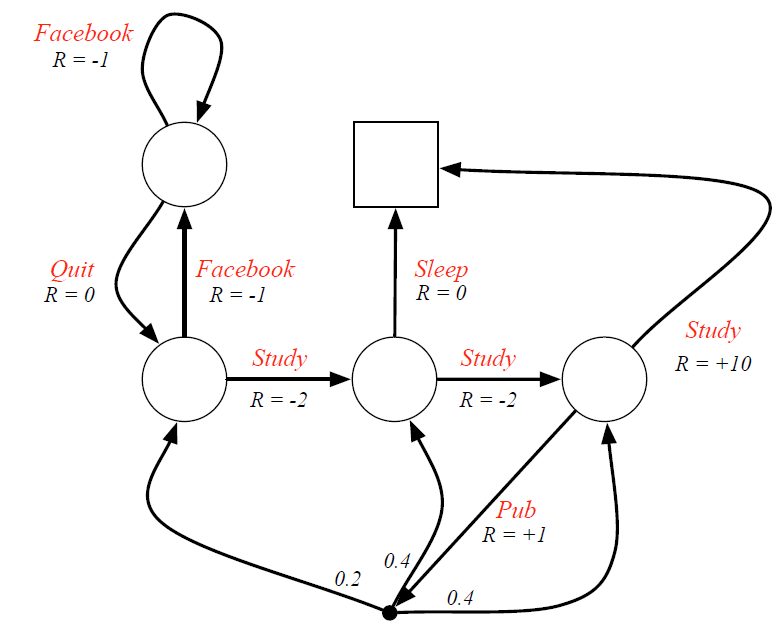
- 这里箭头上的文字表示采取的行为,而不是之前的状态名。
- 即时奖励与行为对应,同一状态下采取不同行为得到的即时奖励不同,即针对 ⟨ S ⟩ \langle{\mathcal{S}}\rangle ⟨S⟩的奖励变成了针对 ⟨ S , A ⟩ \langle{\mathcal{S}},{\mathcal{A}}\rangle ⟨S,A⟩的奖励
- 为了避免混淆,此图没有给出各状态的名称,只给了各行为的名称。
- 当选择“查阅文献”这一动作时,主动进入了一个临时状态(实心黑点),此时环境按照动力学分配到另外三个状态,agent无权决定
(6)状态价值函数
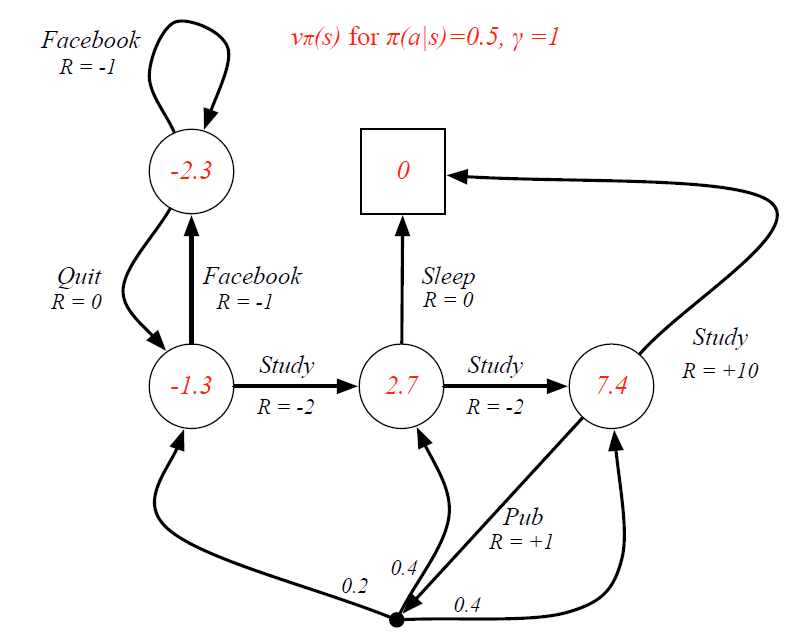
(7)Bellman期望方程
1)求状态价值函数
这里取
π
(
a
∣
s
)
=
0.5
,
γ
=
1
\pi(a\vert s)=0.5,\gamma=1
π(a∣s)=0.5,γ=1
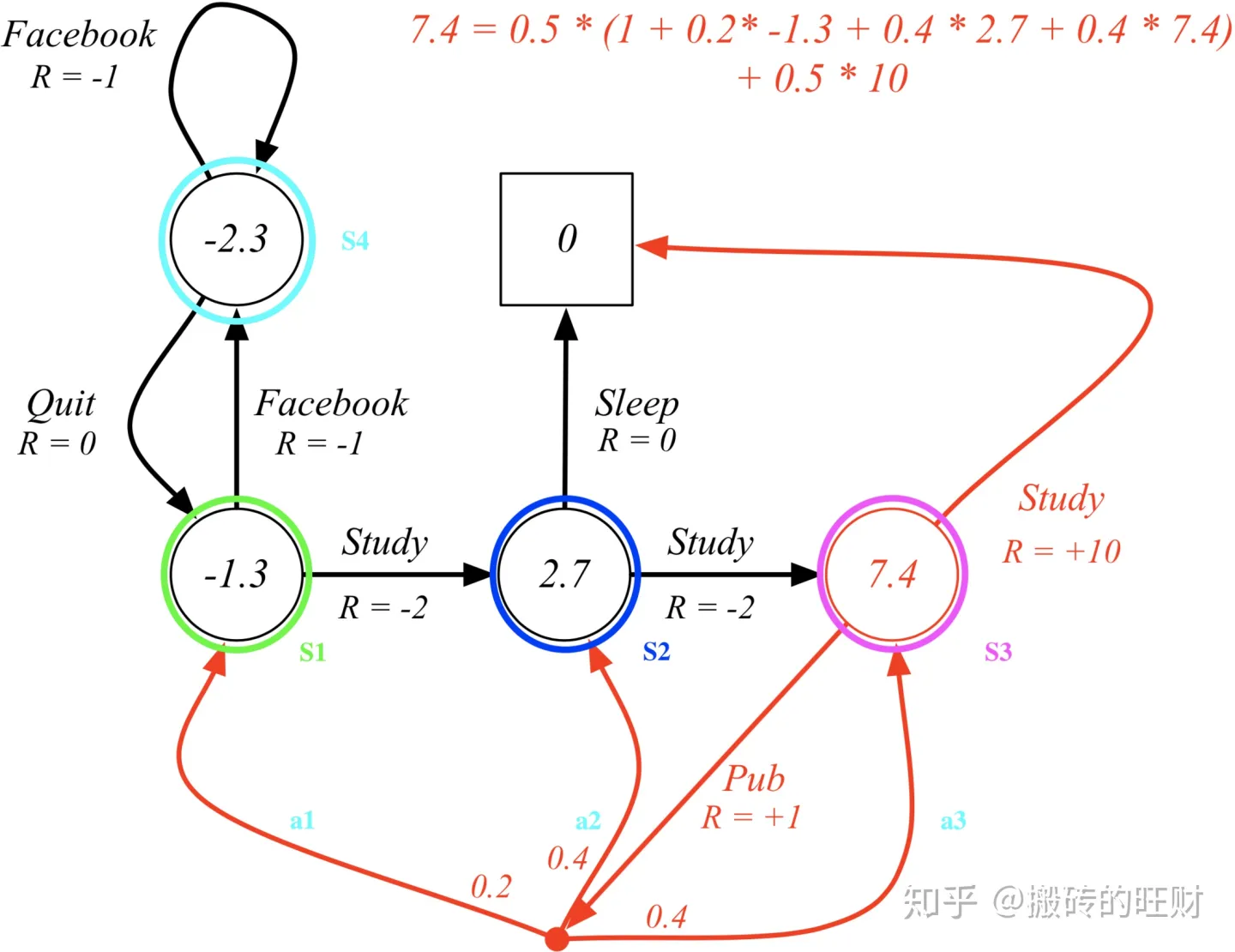
对于终点位置:没有下一个状态,也没有当前状态下的动作,因此状态价值函数为0
对于状态S1,S2,S3,S4,依次定义价值为 v 1 , v 2 , v 3 , v 4 v_1,v_2,v_3,v_4 v1,v2,v3,v4,根据KaTeX parse error: Expected group after '_' at position 14: v_\pi(s)=\sum_̲\limits {a\in\m…可以计算得到:
- 状态S1: v 1 = π ( S t u d y ∣ S 1 ) × ( R S 1 S t u d y + γ v 2 ) + π ( F a c e b o o k ∣ S 1 ) × ( R S 1 F a c e b o o k + γ v 4 ) = 0.5 × ( − 2 + 1 × v 2 ) + 0.5 × ( − 1 + 1 × v 4 ) = − 1.5 + 0.5 v 2 + 0.5 v 4 v_1 =\pi(Study\vert S1)\times (R_{S1}^{Study}+\gamma v_2)+\pi(Facebook\vert S1)\times(R_{S1}^{Facebook}+\gamma v_4) = 0.5\times (-2+1\times v_2)+0.5\times (-1+1\times v_4) = -1.5 + 0.5v_2+0.5v_4 v1=π(Study∣S1)×(RS1Study+γv2)+π(Facebook∣S1)×(RS1Facebook+γv4)=0.5×(−2+1×v2)+0.5×(−1+1×v4)=−1.5+0.5v2+0.5v4
- 状态S2 v 2 = π ( S t u d y ∣ S 2 ) × ( R S 2 S t u d y + γ v 3 ) + π ( S l e e p ∣ S 2 ) × ( R S 2 S l e e p + γ v e n d ) = 0.5 × ( − 2 + 1 × v 3 ) + 0.5 × ( 0 + 1 × 0 ) = 0.5 v 3 − 1 v_2 =\pi(Study\vert S2)\times (R_{S2}^{Study}+\gamma v_3)+\pi(Sleep\vert S2)\times(R_{S2}^{Sleep}+\gamma v_{end}) = 0.5\times (-2+1\times v_3)+0.5\times (0+1\times 0) = 0.5v_3 - 1 v2=π(Study∣S2)×(RS2Study+γv3)+π(Sleep∣S2)×(RS2Sleep+γvend)=0.5×(−2+1×v3)+0.5×(0+1×0)=0.5v3−1
- 状态S3 v 3 = π ( S t u d y ∣ S 3 ) × ( R S 3 S t u d y + γ v 1 ) + π ( P u b ∣ S 3 ) × ( R S 3 P u b + γ ( 0.2 × v 1 + 0.4 × v 2 + 0.4 × v 3 ) ) = 0.5 × ( 10 + 1 × 0 ) + 0.5 × ( 1 + 1 × ( 0.2 × v 1 + 0.4 × v 2 + 0.4 × v 3 ) ) = 5.5 + 0.1 v 1 + 0.2 v 2 + 0.2 v 3 v_3 =\pi(Study\vert S3)\times (R_{S3}^{Study}+\gamma v_1)+\pi(Pub\vert S3)\times(R_{S3}^{Pub}+\gamma (0.2\times v_1+0.4\times v_2 + 0.4\times v_3)) = 0.5\times (10+1\times 0)+0.5\times (1+1\times (0.2\times v_1+0.4\times v_2 + 0.4\times v_3)) =5.5+0.1v1+0.2v2+0.2v3 v3=π(Study∣S3)×(RS3Study+γv1)+π(Pub∣S3)×(RS3Pub+γ(0.2×v1+0.4×v2+0.4×v3))=0.5×(10+1×0)+0.5×(1+1×(0.2×v1+0.4×v2+0.4×v3))=5.5+0.1v1+0.2v2+0.2v3
- 状态S4
v
4
=
π
(
Q
u
i
t
∣
S
4
)
×
(
R
S
4
Q
u
i
t
+
γ
v
3
)
+
π
(
F
a
c
e
b
o
o
k
∣
S
4
)
×
(
R
S
4
F
a
c
e
b
o
o
k
+
γ
v
4
)
=
0.5
×
(
0
+
1
×
v
1
)
+
0.5
×
(
−
1
+
1
×
v
4
)
=
0.5
v
1
+
0.5
v
4
−
0.5
v_4 =\pi(Quit\vert S4)\times (R_{S4}^{Quit}+\gamma v_3)+\pi(Facebook\vert S4)\times(R_{S4}^{Facebook}+\gamma v_4) = 0.5\times (0+1\times v_1)+0.5\times (-1+1\times v_4) = 0.5v_1 + 0.5v_4 - 0.5
v4=π(Quit∣S4)×(RS4Quit+γv3)+π(Facebook∣S4)×(RS4Facebook+γv4)=0.5×(0+1×v1)+0.5×(−1+1×v4)=0.5v1+0.5v4−0.5
可以得到关于 v 1 , v 2 , v 3 , v 4 v_1,v_2,v_3,v_4 v1,v2,v3,v4的方程组:
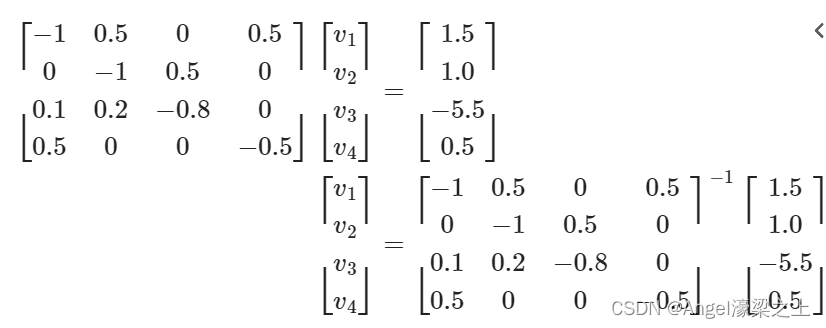
运用python求解该方程:
# coding:utf-8
import numpy as np
np.set_printoptions(precision=3, threshold=np.inf, linewidth=400, suppress=True)
a = np.array([[-1,0.5,0,0.5],[0,-1,0.5,0],[0.1,0.2,-0.8,0],[0.5,0,0,-0.5]])
b = np.array([[1.5],[1.0],[-5.5],[0.5]])
c = np.dot(np.linalg.inv(a), b)
print("c=\n{}".format(c)) # c=[[-1.308] [ 2.692] [ 7.385] [-2.308]]
求解得到 v 1 = − 1.3 , v 2 = 2.7 , v 3 = 7.4 , v 4 = − 2.3 v_1=-1.3,v_2=2.7,v_3=7.4,v_4=-2.3 v1=−1.3,v2=2.7,v3=7.4,v4=−2.3
2)求解动作价值函数
利用公式KaTeX parse error: Expected group after '_' at position 39: …s^a+\gamma \sum_̲\limits {s\in S…
q
π
(
S
1
,
S
t
u
d
y
)
=
R
S
1
S
t
u
d
y
+
γ
P
S
1
S
2
S
t
u
d
y
v
π
(
S
2
)
=
−
2
+
2.7
=
0.7
q_\pi(S1,Study)=\mathcal{R}_{S1}^{Study}+\gamma \mathcal{P}_{S1S2}^{Study}v_\pi(S2)=-2+2.7=0.7
qπ(S1,Study)=RS1Study+γPS1S2Studyvπ(S2)=−2+2.7=0.7
q
π
(
S
1
,
F
a
c
e
b
o
o
k
)
=
R
S
1
F
a
c
e
b
o
o
k
+
γ
P
S
1
S
4
F
a
c
e
b
o
o
k
v
π
(
S
4
)
=
−
1
−
2.3
=
−
3.3
q_\pi(S1,Facebook)=\mathcal{R}_{S1}^{Facebook}+\gamma \mathcal{P}_{S1S4}^{Facebook}v_\pi(S4)=-1-2.3=-3.3
qπ(S1,Facebook)=RS1Facebook+γPS1S4Facebookvπ(S4)=−1−2.3=−3.3
q
π
(
S
2
,
S
l
e
e
p
)
=
R
S
2
S
l
e
e
p
+
γ
P
S
2
e
n
d
S
l
e
e
p
v
π
(
e
n
d
)
=
0
+
0
=
0
q_\pi(S2,Sleep)=\mathcal{R}_{S2}^{Sleep}+\gamma \mathcal{P}_{S2end}^{Sleep}v_\pi(end)=0+0=0
qπ(S2,Sleep)=RS2Sleep+γPS2endSleepvπ(end)=0+0=0
q
π
(
S
2
,
S
t
u
d
y
)
=
R
S
2
S
t
u
d
y
+
γ
P
S
2
S
3
S
t
u
d
y
v
π
(
S
3
)
=
−
2
+
7.4
=
5.4
q_\pi(S2,Study)=\mathcal{R}_{S2}^{Study}+\gamma \mathcal{P}_{S2S3}^{Study}v_\pi(S3)=-2+7.4=5.4
qπ(S2,Study)=RS2Study+γPS2S3Studyvπ(S3)=−2+7.4=5.4
q
π
(
S
3
,
S
t
u
d
y
)
=
R
S
3
S
t
u
d
y
+
γ
P
S
3
e
n
d
S
t
u
d
y
v
π
(
e
n
d
)
=
10
+
0
=
10
q_\pi(S3,Study)=\mathcal{R}_{S3}^{Study}+\gamma \mathcal{P}_{S3end}^{Study}v_\pi(end)=10+0=10
qπ(S3,Study)=RS3Study+γPS3endStudyvπ(end)=10+0=10
q
π
(
S
3
,
P
u
b
)
=
R
S
3
P
u
b
+
γ
∑
s
′
∈
S
P
S
3
⋅
P
u
b
v
π
(
⋅
)
=
1
+
0.2
×
(
−
1.3
)
+
0.4
×
(
2.7
)
+
0.2
×
(
7.4
)
=
4.78
q_\pi(S3,Pub)=\mathcal{R}_{S3}^{Pub}+\gamma \sum \limits _{s^{\prime}\in \mathcal{S}}\mathcal{P}_{S3\cdot}^{Pub}v\pi(\cdot)=1+0.2\times (-1.3)+0.4\times (2.7)+0.2\times (7.4)=4.78
qπ(S3,Pub)=RS3Pub+γs′∈S∑PS3⋅Pubvπ(⋅)=1+0.2×(−1.3)+0.4×(2.7)+0.2×(7.4)=4.78
q
π
(
S
4
,
F
a
c
e
b
o
o
k
)
=
R
S
4
F
a
c
e
b
o
o
k
+
γ
P
S
4
S
4
F
a
c
e
b
o
o
k
v
π
(
S
4
)
=
−
1
+
(
−
2.3
)
=
−
3.3
q_\pi(S4,Facebook)=\mathcal{R}_{S4}^{Facebook}+\gamma \mathcal{P}_{S4S4}^{Facebook}v_\pi(S4)=-1+(-2.3)=-3.3
qπ(S4,Facebook)=RS4Facebook+γPS4S4Facebookvπ(S4)=−1+(−2.3)=−3.3
q
π
(
S
4
,
Q
u
i
t
)
=
R
S
4
Q
u
i
t
+
γ
P
S
4
S
1
Q
u
i
t
v
π
(
S
1
)
=
0
+
(
−
1.3
)
=
−
1.3
q_\pi(S4,Quit)=\mathcal{R}_{S4}^{Quit}+\gamma \mathcal{P}_{S4S1}^{Quit}v_\pi(S1)=0+(-1.3)=-1.3
qπ(S4,Quit)=RS4Quit+γPS4S1Quitvπ(S1)=0+(−1.3)=−1.3
(8)用矩阵形式求解
这里取
π
(
a
∣
s
)
=
0.5
,
γ
=
1
\pi(a\vert s)=0.5,\gamma=1
π(a∣s)=0.5,γ=1

用python求解该方程:
# coding:utf-8
import numpy as np
np.set_printoptions(precision=3, threshold=np.inf, linewidth=400, suppress=True)
gamma = 1.0
E = np.eye(5)
P = np.array(
[[0,0.5,0,0.5,0],
[0,0,0.5,0,0.5],
[0.1,0.2,0.2,0,0.5],
[0.5,0,0,0.5,0],
[0,0,0,0,1]])
R = np.array([[-1.5],[-1],[5.5],[-0.5],[0]])
# print(np.linalg.det(E-gamma*P))
# np.linalg.det(E-gamma*P)=0.0 --> E-gamma*P是奇异矩阵
# 给矩阵主对角线每一个元素加一个很小的量,如1e-6,使其强制可逆
# print(np.linalg.det(E*1e-6+E-gamma*P))
# np.linalg.det(E*1e-6+E-gamma*P)=1.6250e-07
v = np.dot(np.linalg.inv(E*1e-6+E-gamma*P), R)
print("v=\n{}".format(v)) # v=[[-1.308] [ 2.692] [ 7.385] [-2.308] [ 0. ]]
(9)最优价值函数
最优状态价值:

最优动作价值:
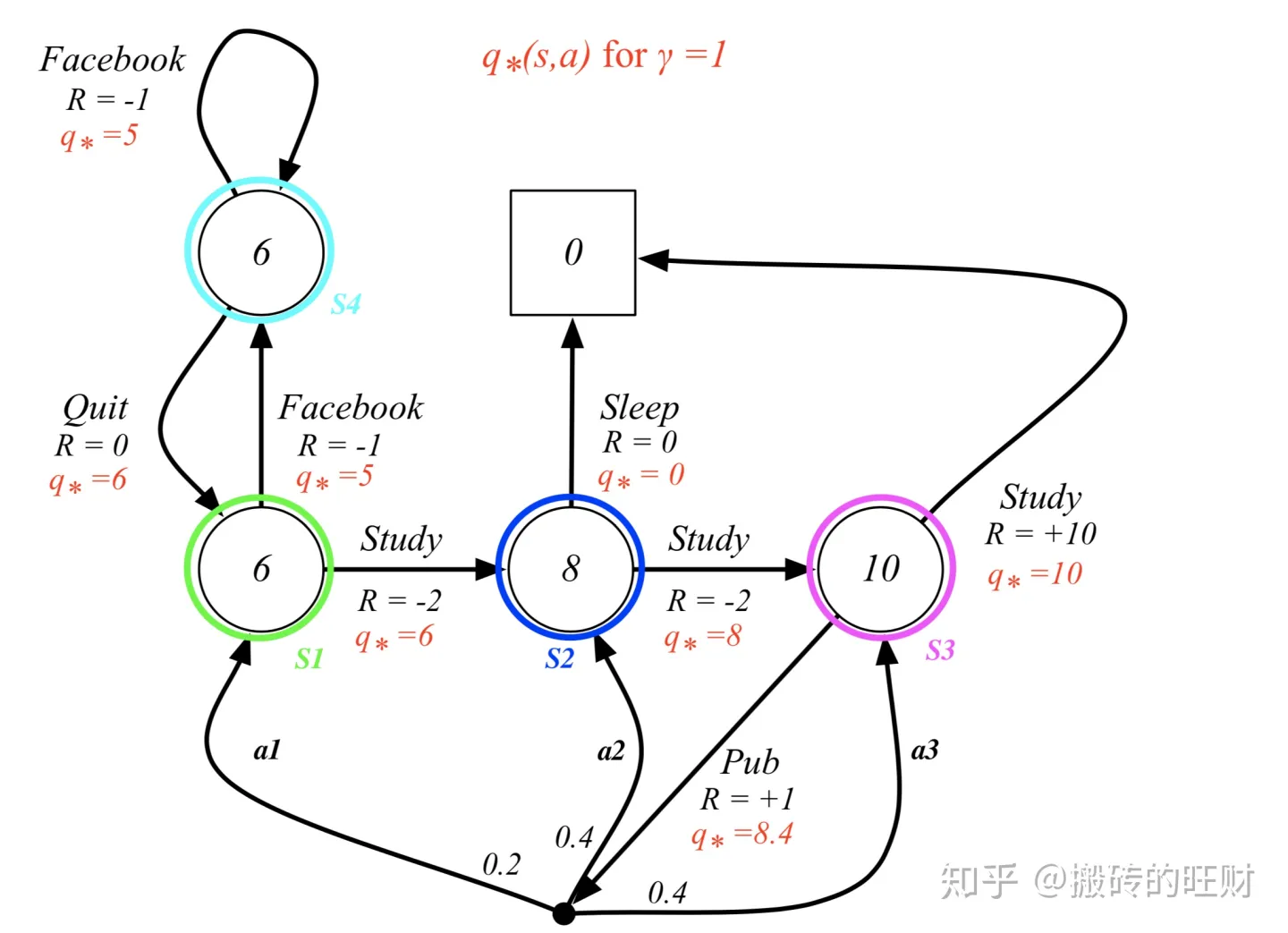
(10)最优策略
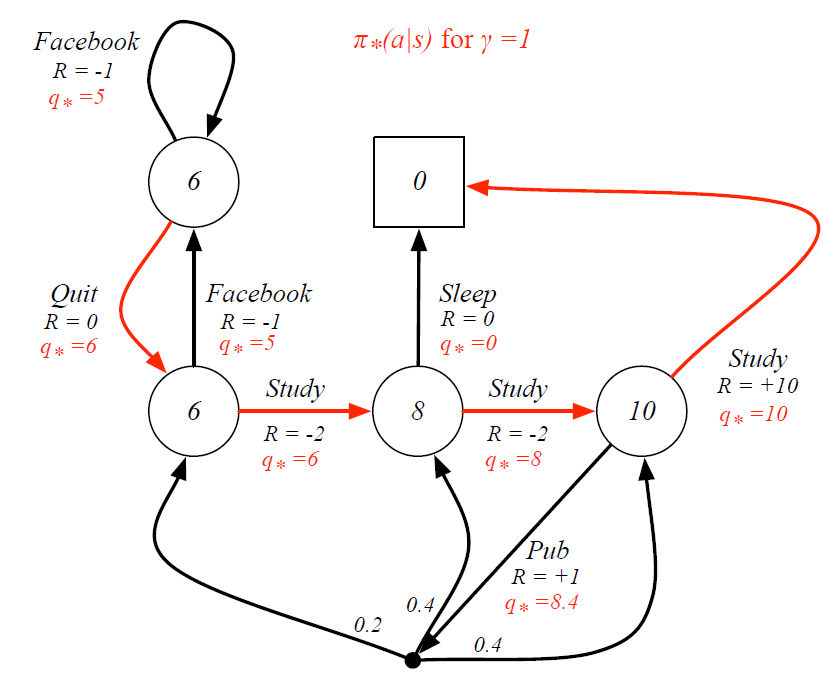
(11)贝尔曼最优方程求解
已知KaTeX parse error: Expected group after '_' at position 39: …s^a+\gamma \sum_̲\limits {s\in S…
q
∗
(
s
,
a
)
=
max
π
q
π
(
s
,
a
)
q_*(s,a)=\max \limits_\pi q_\pi(s,a)
q∗(s,a)=πmaxqπ(s,a)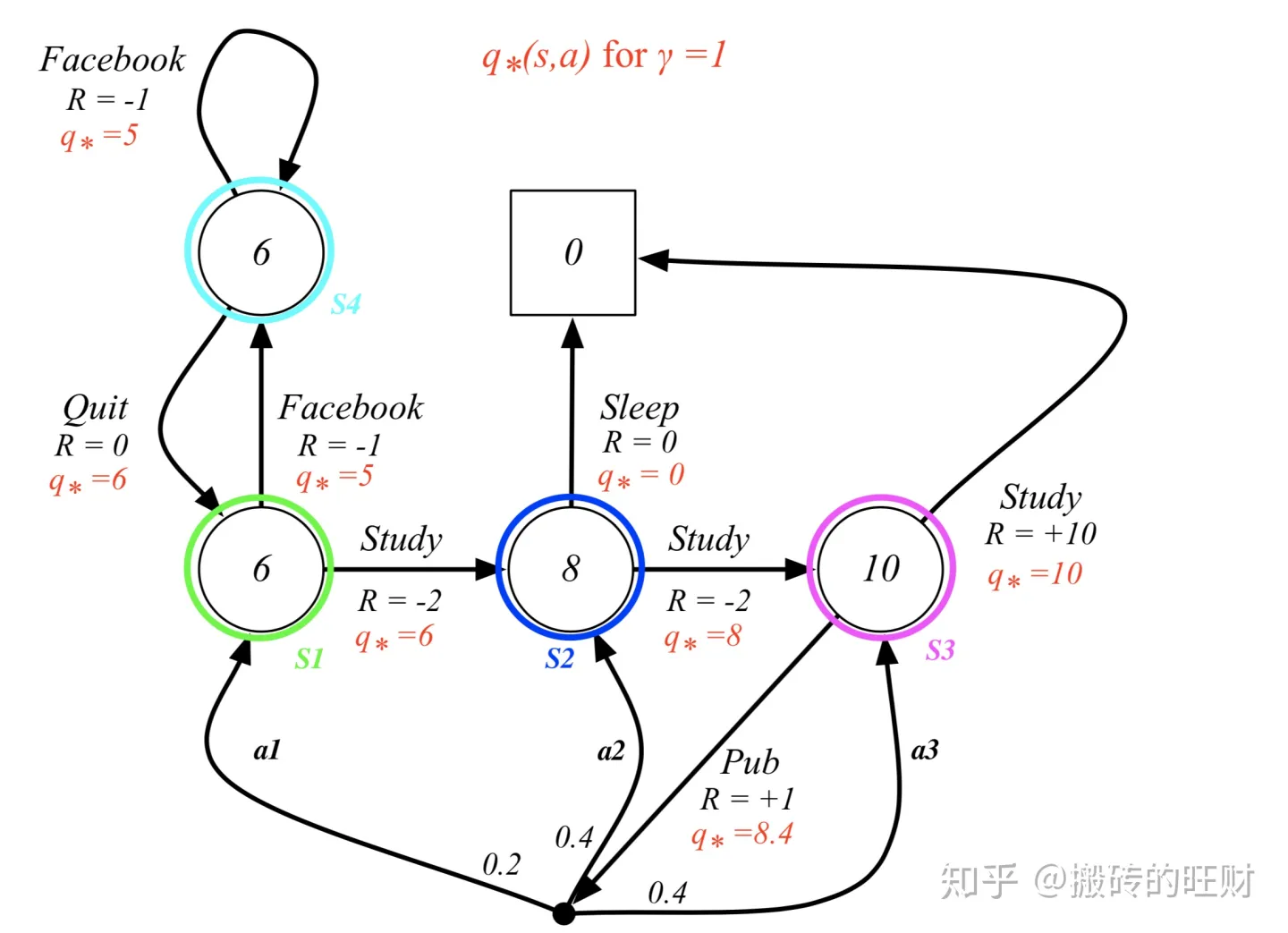
求解:
q
∗
(
S
1
,
S
t
u
d
y
)
=
R
S
1
S
t
u
d
y
+
γ
P
S
1
S
2
S
t
u
d
y
max
a
′
q
∗
(
S
2
,
a
′
)
=
R
S
1
S
t
u
d
y
+
γ
P
S
1
S
2
S
t
u
d
y
max
(
q
∗
(
S
2
,
S
l
e
e
p
)
,
q
∗
(
S
2
,
S
t
u
d
y
)
)
=
−
2
+
m
a
x
(
0
,
q
∗
(
S
2
,
S
t
u
d
y
)
)
q_*(S1,Study)=\mathcal{R}_{S1}^{Study}+\gamma \mathcal{P}_{S1S2}^{Study}\max \limits_{a^{\prime}}q_*(S2,a^{\prime}) \\ =\mathcal{R}_{S1}^{Study}+\gamma \mathcal{P}_{S1S2}^{Study}\max (q_*(S2,Sleep),q_*(S2,Study)) \\ = -2+max(0,q_*(S2,Study))
q∗(S1,Study)=RS1Study+γPS1S2Studya′maxq∗(S2,a′)=RS1Study+γPS1S2Studymax(q∗(S2,Sleep),q∗(S2,Study))=−2+max(0,q∗(S2,Study))
q
∗
(
S
1
,
F
a
c
e
b
o
o
k
)
=
R
S
1
F
a
c
e
b
o
o
k
+
γ
P
S
1
S
4
F
a
c
e
b
o
o
k
max
a
′
q
∗
(
S
4
,
a
′
)
=
R
S
1
F
a
c
e
b
o
o
k
+
γ
P
S
1
S
4
F
a
c
e
b
o
o
k
max
(
q
∗
(
S
4
,
F
a
c
e
b
o
o
k
)
,
q
∗
(
S
4
,
Q
u
i
t
)
)
=
−
1
+
max
(
q
∗
(
S
4
,
F
a
c
e
b
o
o
k
)
,
q
∗
(
S
4
,
Q
u
i
t
)
)
q_*(S1,Facebook)=\mathcal{R}_{S1}^{Facebook}+\gamma \mathcal{P}_{S1S4}^{Facebook}\max \limits_{a^{\prime}}q_*(S4,a^{\prime}) \\ =\mathcal{R}_{S1}^{Facebook}+\gamma \mathcal{P}_{S1S4}^{Facebook}\max (q_*(S4,Facebook),q_*(S4,Quit)) \\ = -1+\max (q_*(S4,Facebook),q_*(S4,Quit))
q∗(S1,Facebook)=RS1Facebook+γPS1S4Facebooka′maxq∗(S4,a′)=RS1Facebook+γPS1S4Facebookmax(q∗(S4,Facebook),q∗(S4,Quit))=−1+max(q∗(S4,Facebook),q∗(S4,Quit))
q
∗
(
S
2
,
S
t
u
d
y
)
=
R
S
1
S
t
u
d
y
+
γ
P
S
2
S
3
S
t
u
d
y
max
a
′
q
∗
(
S
3
,
a
′
)
=
R
S
1
S
t
u
d
y
+
γ
P
S
2
S
3
S
t
u
d
y
max
(
q
∗
(
S
3
,
S
t
u
d
y
)
,
q
∗
(
S
3
,
P
u
b
)
)
=
−
2
+
max
(
q
∗
(
S
3
,
S
t
u
d
y
)
,
q
∗
(
S
3
,
P
u
b
)
)
q_*(S2,Study)=\mathcal{R}_{S1}^{Study}+\gamma \mathcal{P}_{S2S3}^{Study}\max \limits_{a^{\prime}}q_*(S3,a^{\prime}) \\ =\mathcal{R}_{S1}^{Study}+\gamma \mathcal{P}_{S2S3}^{Study}\max (q_*(S3,Study),q_*(S3,Pub)) \\ = -2+\max (q_*(S3,Study),q_*(S3,Pub))
q∗(S2,Study)=RS1Study+γPS2S3Studya′maxq∗(S3,a′)=RS1Study+γPS2S3Studymax(q∗(S3,Study),q∗(S3,Pub))=−2+max(q∗(S3,Study),q∗(S3,Pub))
q
∗
(
S
2
,
S
l
e
e
p
)
=
R
S
2
S
l
e
e
p
+
γ
P
S
2
e
n
d
S
l
e
e
p
v
(
e
n
d
)
=
0
+
0
=
0
q_*(S2,Sleep)=\mathcal{R}_{S2}^{Sleep}+\gamma \mathcal{P}_{S2end}^{Sleep}v(end)=0+0=0
q∗(S2,Sleep)=RS2Sleep+γPS2endSleepv(end)=0+0=0
q
∗
(
S
3
,
S
t
u
d
y
)
=
R
S
3
S
t
u
d
y
+
γ
P
S
3
e
n
d
S
t
u
d
y
v
(
e
n
d
)
=
10
+
0
=
10
q_*(S3,Study)=\mathcal{R}_{S3}^{Study}+\gamma \mathcal{P}_{S3end}^{Study}v(end)=10+0=10
q∗(S3,Study)=RS3Study+γPS3endStudyv(end)=10+0=10
q
∗
(
S
3
,
P
u
b
)
=
R
S
3
P
u
b
+
γ
P
S
3
⋅
P
u
b
max
a
′
q
∗
(
⋅
,
a
′
)
=
R
S
3
P
u
b
+
γ
(
P
⋅
S
1
a
1
max
(
q
∗
(
S
1
,
F
a
c
e
b
o
o
k
)
,
q
∗
(
S
1
,
S
t
u
d
y
)
)
+
P
⋅
S
2
a
2
max
(
q
∗
(
S
2
,
S
l
e
e
p
)
,
q
∗
(
S
2
,
S
t
u
d
y
)
)
+
P
⋅
S
3
a
3
max
(
q
∗
(
S
3
,
P
u
b
)
,
q
∗
(
S
3
,
S
t
u
d
y
)
)
)
=
1
+
0.2
×
max
(
(
q
∗
(
S
1
,
S
t
u
d
y
)
,
q
∗
(
S
1
,
F
a
c
e
b
o
o
k
)
)
+
0.4
×
max
(
(
q
∗
(
S
2
,
S
l
e
e
p
)
,
q
∗
(
S
2
,
S
t
u
d
y
)
)
+
0.4
×
max
(
(
q
∗
(
S
3
,
P
u
b
)
,
q
∗
(
S
3
,
S
t
u
d
y
)
)
q_*(S3,Pub)=\mathcal{R}_{S3}^{Pub}+\gamma \mathcal{P}_{S3\cdot}^{Pub}\max \limits_{a^{\prime}}q_*(\cdot,a^{\prime}) \\ =\mathcal{R}_{S3}^{Pub}+\gamma (\mathcal{P}_{\cdot S1}^{a1}\max (q_*(S1,Facebook),q_*(S1,Study))+\mathcal{P}_{\cdot S2}^{a2}\max (q_*(S2,Sleep),q_*(S2,Study)) + \mathcal{P}_{\cdot S3}^{a3}\max (q_*(S3,Pub),q_*(S3,Study)))\\ = 1+0.2\times\max ((q_*(S1,Study),q_*(S1,Facebook))+0.4\times\max ((q_*(S2,Sleep),q_*(S2,Study))+0.4\times\max ((q_*(S3,Pub),q_*(S3,Study)) \\
q∗(S3,Pub)=RS3Pub+γPS3⋅Puba′maxq∗(⋅,a′)=RS3Pub+γ(P⋅S1a1max(q∗(S1,Facebook),q∗(S1,Study))+P⋅S2a2max(q∗(S2,Sleep),q∗(S2,Study))+P⋅S3a3max(q∗(S3,Pub),q∗(S3,Study)))=1+0.2×max((q∗(S1,Study),q∗(S1,Facebook))+0.4×max((q∗(S2,Sleep),q∗(S2,Study))+0.4×max((q∗(S3,Pub),q∗(S3,Study))
q
∗
(
S
4
,
F
a
c
e
b
o
o
k
)
=
R
S
4
F
a
c
e
b
o
o
k
+
γ
P
S
4
S
4
F
a
c
e
b
o
o
k
max
a
′
q
∗
(
S
4
,
a
′
)
=
R
S
4
F
a
c
e
b
o
o
k
+
γ
P
S
4
S
4
F
a
c
e
b
o
o
k
max
(
q
∗
(
S
4
,
F
a
c
e
b
o
o
k
)
,
q
∗
(
S
4
,
Q
u
i
t
)
)
=
−
1
+
max
(
q
∗
(
S
4
,
F
a
c
e
b
o
o
k
)
,
q
∗
(
S
4
,
Q
u
i
t
)
)
q_*(S4,Facebook)=\mathcal{R}_{S4}^{Facebook}+\gamma \mathcal{P}_{S4S4}^{Facebook}\max \limits_{a^{\prime}}q_*(S4,a^{\prime}) \\ =\mathcal{R}_{S4}^{Facebook}+\gamma \mathcal{P}_{S4S4}^{Facebook}\max (q_*(S4,Facebook),q_*(S4,Quit)) \\ = -1+\max (q_*(S4,Facebook),q_*(S4,Quit))
q∗(S4,Facebook)=RS4Facebook+γPS4S4Facebooka′maxq∗(S4,a′)=RS4Facebook+γPS4S4Facebookmax(q∗(S4,Facebook),q∗(S4,Quit))=−1+max(q∗(S4,Facebook),q∗(S4,Quit))
q
∗
(
S
4
,
Q
u
i
t
)
=
R
S
4
Q
u
i
t
+
γ
P
S
4
S
1
Q
u
i
t
max
a
′
q
∗
(
S
1
,
a
′
)
=
R
S
4
Q
u
i
t
+
γ
P
S
4
S
1
Q
u
i
t
max
(
q
∗
(
S
1
,
S
t
u
d
y
)
,
q
∗
(
S
1
,
F
a
c
e
b
o
o
k
)
)
=
0
+
max
(
q
∗
(
S
1
,
S
t
u
d
y
)
,
q
∗
(
S
1
,
F
a
c
e
b
o
o
k
)
)
q_*(S4,Quit)=\mathcal{R}_{S4}^{Quit}+\gamma \mathcal{P}_{S4S1}^{Quit}\max \limits_{a^{\prime}}q_*(S1,a^{\prime}) \\ =\mathcal{R}_{S4}^{Quit}+\gamma \mathcal{P}_{S4S1}^{Quit}\max (q_*(S1,Study),q_*(S1,Facebook)) \\ = 0+\max (q_*(S1,Study),q_*(S1,Facebook))
q∗(S4,Quit)=RS4Quit+γPS4S1Quita′maxq∗(S1,a′)=RS4Quit+γPS4S1Quitmax(q∗(S1,Study),q∗(S1,Facebook))=0+max(q∗(S1,Study),q∗(S1,Facebook))
整理可得:
q
∗
(
S
1
,
S
t
u
d
y
)
=
−
2
+
m
a
x
(
0
,
q
∗
(
S
2
,
S
t
u
d
y
)
)
q
∗
(
S
1
,
F
a
c
e
b
o
o
k
)
=
−
1
+
max
(
q
∗
(
S
4
,
F
a
c
e
b
o
o
k
)
,
q
∗
(
S
4
,
Q
u
i
t
)
)
q
∗
(
S
2
,
S
l
e
e
p
)
=
0
q
∗
(
S
2
,
S
t
u
d
y
)
=
−
2
+
max
(
10
,
q
∗
(
S
3
,
P
u
b
)
)
q
∗
(
S
3
,
S
t
u
d
y
)
=
10
q
∗
(
S
3
,
P
u
b
)
=
1
+
0.2
×
max
(
(
q
∗
(
S
1
,
S
t
u
d
y
)
,
q
∗
(
S
1
,
F
a
c
e
b
o
o
k
)
)
+
0.4
×
max
(
0
,
q
∗
(
S
2
,
S
t
u
d
y
)
)
+
0.4
×
max
(
(
q
∗
(
S
3
,
P
u
b
)
,
10
)
q
∗
(
S
4
,
F
a
c
e
b
o
o
k
)
=
−
1
+
max
(
q
∗
(
S
4
,
F
a
c
e
b
o
o
k
)
,
q
∗
(
S
4
,
Q
u
i
t
)
)
q
∗
(
S
4
,
Q
u
i
t
)
=
0
+
max
(
q
∗
(
S
1
,
S
t
u
d
y
)
,
q
∗
(
S
1
,
F
a
c
e
b
o
o
k
)
)
q_*(S1,Study) = -2+max(0,q_*(S2,Study))\\ q_*(S1,Facebook)=-1+\max (q_*(S4,Facebook),q_*(S4,Quit))\\ q_*(S2,Sleep) = 0\\ q_*(S2,Study) = -2+\max (10,q_*(S3,Pub)) \\ q_*(S3,Study) = 10\\ q_*(S3,Pub)=1+0.2\times\max ((q_*(S1,Study),q_*(S1,Facebook))+0.4\times\max (0,q_*(S2,Study))+0.4\times\max ((q_*(S3,Pub),10)\\ q_*(S4,Facebook)=-1+\max (q_*(S4,Facebook),q_*(S4,Quit))\\ q_*(S4,Quit)= 0+\max (q_*(S1,Study),q_*(S1,Facebook))
q∗(S1,Study)=−2+max(0,q∗(S2,Study))q∗(S1,Facebook)=−1+max(q∗(S4,Facebook),q∗(S4,Quit))q∗(S2,Sleep)=0q∗(S2,Study)=−2+max(10,q∗(S3,Pub))q∗(S3,Study)=10q∗(S3,Pub)=1+0.2×max((q∗(S1,Study),q∗(S1,Facebook))+0.4×max(0,q∗(S2,Study))+0.4×max((q∗(S3,Pub),10)q∗(S4,Facebook)=−1+max(q∗(S4,Facebook),q∗(S4,Quit))q∗(S4,Quit)=0+max(q∗(S1,Study),q∗(S1,Facebook))
简单观察可得:
q
∗
(
S
2
,
S
t
u
d
y
)
≥
8
q
∗
(
S
1
,
S
t
u
d
y
)
≥
6
q
∗
(
S
3
,
P
u
b
)
=
1
+
0.2
×
max
(
(
q
∗
(
S
1
,
S
t
u
d
y
)
,
q
∗
(
S
1
,
F
a
c
e
b
o
o
k
)
)
+
0.4
×
q
∗
(
S
2
,
S
t
u
d
y
)
+
0.4
×
max
(
(
q
∗
(
S
3
,
P
u
b
)
,
10
)
q_*(S2,Study) \geq 8 \\ q_*(S1,Study) \geq 6\\ q_*(S3,Pub) = 1+0.2\times\max ((q_*(S1,Study),q_*(S1,Facebook))+0.4\times q_*(S2,Study)+0.4\times\max ((q_*(S3,Pub),10)\\
q∗(S2,Study)≥8q∗(S1,Study)≥6q∗(S3,Pub)=1+0.2×max((q∗(S1,Study),q∗(S1,Facebook))+0.4×q∗(S2,Study)+0.4×max((q∗(S3,Pub),10)
观察
q
∗
(
S
4
,
F
a
c
e
b
o
o
k
)
=
−
1
+
max
(
q
∗
(
S
4
,
F
a
c
e
b
o
o
k
)
,
q
∗
(
S
4
,
Q
u
i
t
)
)
q_*(S4,Facebook)=-1+\max (q_*(S4,Facebook),q_*(S4,Quit))
q∗(S4,Facebook)=−1+max(q∗(S4,Facebook),q∗(S4,Quit)),显然
q
∗
(
S
4
,
F
a
c
e
b
o
o
k
)
=
−
1
+
q
∗
(
S
4
,
Q
u
i
t
)
q_*(S4,Facebook)=-1+q_*(S4,Quit)
q∗(S4,Facebook)=−1+q∗(S4,Quit)
则
q
∗
(
S
1
,
F
a
c
e
b
o
o
k
)
=
−
1
+
q
∗
(
S
4
,
Q
u
i
t
)
q
∗
(
S
4
,
Q
u
i
t
)
=
0
+
max
(
q
∗
(
S
1
,
S
t
u
d
y
)
,
−
1
+
q
∗
(
S
4
,
Q
u
i
t
)
)
=
q
∗
(
S
1
,
S
t
u
d
y
)
q
∗
(
S
3
,
P
u
b
)
=
1
+
0.2
×
max
(
(
q
∗
(
S
1
,
S
t
u
d
y
)
,
q
∗
(
S
1
,
F
a
c
e
b
o
o
k
)
)
+
0.4
×
q
∗
(
S
2
,
S
t
u
d
y
)
+
0.4
×
max
(
(
q
∗
(
S
3
,
P
u
b
)
,
10
)
=
1
+
0.2
×
max
(
(
q
∗
(
S
4
,
Q
u
i
t
)
,
−
1
+
q
∗
(
S
4
,
Q
u
i
t
)
)
+
0.4
×
q
∗
(
S
2
,
S
t
u
d
y
)
+
0.4
×
max
(
(
q
∗
(
S
3
,
P
u
b
)
,
10
)
=
1
+
0.2
×
q
∗
(
S
4
,
Q
u
i
t
)
+
0.4
×
q
∗
(
S
2
,
S
t
u
d
y
)
+
0.4
×
max
(
(
q
∗
(
S
3
,
P
u
b
)
,
10
)
=
1
+
0.2
×
q
∗
(
S
1
,
S
t
u
d
y
)
+
0.4
×
q
∗
(
S
2
,
S
t
u
d
y
)
+
0.4
×
max
(
(
q
∗
(
S
3
,
P
u
b
)
,
10
)
=
1
+
0.2
×
(
−
2
+
q
∗
(
S
2
,
S
t
u
d
y
)
)
+
0.4
×
q
∗
(
S
2
,
S
t
u
d
y
)
+
0.4
×
max
(
(
q
∗
(
S
3
,
P
u
b
)
,
10
)
=
0.6
+
0.6
×
q
∗
(
S
2
,
S
t
u
d
y
)
+
0.4
×
max
(
(
q
∗
(
S
3
,
P
u
b
)
,
10
)
(
n
o
t
e
:
q
∗
(
S
2
,
S
t
u
d
y
)
≥
8
)
)
=
0.6
+
0.6
×
q
∗
(
S
2
,
S
t
u
d
y
)
+
0.4
×
10
=
0.6
×
q
∗
(
S
2
,
S
t
u
d
y
)
+
4.6
q_*(S1,Facebook)=-1+q_*(S4,Quit)\\ q_*(S4,Quit)= 0+\max (q_*(S1,Study),-1+q_*(S4,Quit))=q_*(S1,Study)\\ q_*(S3,Pub)=1+0.2\times\max ((q_*(S1,Study),q_*(S1,Facebook))+0.4\times q_*(S2,Study)+0.4\times\max ((q_*(S3,Pub),10)\\ =1+0.2\times\max ((q_*(S4,Quit),-1+q_*(S4,Quit))+0.4\times q_*(S2,Study)+0.4\times\max ((q_*(S3,Pub),10) \\ =1+0.2\times q_*(S4,Quit)+0.4\times q_*(S2,Study)+0.4\times\max ((q_*(S3,Pub),10)\\ =1+0.2\times q_*(S1,Study)+0.4\times q_*(S2,Study)+0.4\times\max ((q_*(S3,Pub),10)\\ =1+0.2\times (-2+q_*(S2,Study))+0.4\times q_*(S2,Study)+0.4\times\max ((q_*(S3,Pub),10)\\ = 0.6+0.6\times q_*(S2,Study)+0.4\times\max ((q_*(S3,Pub),10) \ \ \ (note:q_*(S2,Study) \geq 8))\\ = 0.6+0.6\times q_*(S2,Study)+0.4\times 10\\ = 0.6\times q_*(S2,Study) + 4.6
q∗(S1,Facebook)=−1+q∗(S4,Quit)q∗(S4,Quit)=0+max(q∗(S1,Study),−1+q∗(S4,Quit))=q∗(S1,Study)q∗(S3,Pub)=1+0.2×max((q∗(S1,Study),q∗(S1,Facebook))+0.4×q∗(S2,Study)+0.4×max((q∗(S3,Pub),10)=1+0.2×max((q∗(S4,Quit),−1+q∗(S4,Quit))+0.4×q∗(S2,Study)+0.4×max((q∗(S3,Pub),10)=1+0.2×q∗(S4,Quit)+0.4×q∗(S2,Study)+0.4×max((q∗(S3,Pub),10)=1+0.2×q∗(S1,Study)+0.4×q∗(S2,Study)+0.4×max((q∗(S3,Pub),10)=1+0.2×(−2+q∗(S2,Study))+0.4×q∗(S2,Study)+0.4×max((q∗(S3,Pub),10)=0.6+0.6×q∗(S2,Study)+0.4×max((q∗(S3,Pub),10) (note:q∗(S2,Study)≥8))=0.6+0.6×q∗(S2,Study)+0.4×10=0.6×q∗(S2,Study)+4.6
总结可得:
q
∗
(
S
1
,
S
t
u
d
y
)
=
−
2
+
8
=
6
q
∗
(
S
1
,
F
a
c
e
b
o
o
k
)
=
−
1
+
6
=
5
q
∗
(
S
2
,
S
l
e
e
p
)
=
0
q
∗
(
S
2
,
S
t
u
d
y
)
=
−
2
+
10
=
8
q
∗
(
S
3
,
S
t
u
d
y
)
=
10
q
∗
(
S
3
,
P
u
b
)
=
0.6
×
8
+
4.6
=
8.4
q
∗
(
S
4
,
F
a
c
e
b
o
o
k
)
=
−
1
+
6
=
5
q
∗
(
S
4
,
Q
u
i
t
)
=
6
q_*(S1,Study) = -2 + 8 =6\\ q_*(S1,Facebook) =-1+6=5\\ q_*(S2,Sleep) = 0\\ q_*(S2,Study) = -2 + 10 = 8 \\ q_*(S3,Study)= 10\\ q_*(S3,Pub)=0.6\times 8 + 4.6=8.4\\ q_*(S4,Facebook)= -1+6=5\\ q_*(S4,Quit)= 6
q∗(S1,Study)=−2+8=6q∗(S1,Facebook)=−1+6=5q∗(S2,Sleep)=0q∗(S2,Study)=−2+10=8q∗(S3,Study)=10q∗(S3,Pub)=0.6×8+4.6=8.4q∗(S4,Facebook)=−1+6=5q∗(S4,Quit)=6
因此,可以求出最优状态价值函数:
v
∗
(
S
1
)
=
6
v
∗
(
S
2
)
=
8
v
∗
(
S
3
)
=
−
2
+
10
=
10
v
∗
(
S
4
)
=
6
v_*(S1) = 6\\ v_*(S2) = 8\\ v_*(S3) = -2 + 10 = 10 \\ v_*(S4)=6\\
v∗(S1)=6v∗(S2)=8v∗(S3)=−2+10=10v∗(S4)=6
6.总结
马尔科夫过程:元组
⟨
S
,
P
⟩
\langle{\mathcal{S}},{\mathcal{P}}\rangle
⟨S,P⟩
马尔科夫奖励过程:元组
⟨
S
,
P
,
R
,
γ
⟩
\langle{\mathcal{S}},\mathcal{P}, {\mathcal{R}},{\mathcal{\gamma}}\rangle
⟨S,P,R,γ⟩
马尔可夫决策过程:元组
⟨
S
,
A
,
P
,
R
,
γ
⟩
\langle{\mathcal{S}},\mathcal{A}, \mathcal{P}, {\mathcal{R}},{\mathcal{\gamma}}\rangle
⟨S,A,P,R,γ⟩
马尔可夫奖励过程的贝尔曼方程:
v
(
s
)
=
E
[
R
t
+
1
+
γ
v
(
S
t
+
1
)
∣
S
t
=
s
]
=
R
s
+
γ
∑
s
′
∈
S
P
S
S
′
v
(
s
′
)
v(s)=\mathbb{E}[R_{t+1}+\gamma v(S_{t+1})\vert S_t=s]=R_s+\gamma \sum_{s^{\prime}\in \mathcal{S}}\mathcal{P}_{SS^{\prime}}v(s^{\prime})
v(s)=E[Rt+1+γv(St+1)∣St=s]=Rs+γ∑s′∈SPSS′v(s′)
马尔科夫决策过程的贝尔曼期望方程:
- 状态-价值函数: v π ( s ) = E [ R t + 1 + γ v π ( S t + 1 ) ∣ S t = s ] = ∑ a ∈ A π ( a ∣ s ) q π ( s , a ) = ∑ a ∈ A π ( a ∣ s ) ( R s a + γ ∑ s ∈ S ′ P S S ′ a v π ( s ′ ) ) v_\pi(s)=\mathbb{E}[R_{t+1}+\gamma v_\pi(S_{t+1})\vert S_t=s]=\sum_ {a\in\mathcal{A}}\pi(a\vert s)q_\pi(s,a)=\sum_ {a\in\mathcal{A}}\pi(a\vert s)(\mathcal{R}_s^a+\gamma \sum_ {s\in S^{\prime}}\mathcal{P}_{SS^{\prime}}^av_\pi(s^{\prime})) vπ(s)=E[Rt+1+γvπ(St+1)∣St=s]=∑a∈Aπ(a∣s)qπ(s,a)=∑a∈Aπ(a∣s)(Rsa+γ∑s∈S′PSS′avπ(s′))
- 动作-价值函数: q π ( s , a ) = E [ R t + 1 + γ q π ( S t + 1 , A t + 1 ) ∣ S t = s , A t = a ] = R s a + γ ∑ s ′ ∈ S P S S ′ a v π ( s ′ ) q_\pi(s,a)=\mathbb{E}[R_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1})\vert S_t=s,A_t=a]=\mathcal{R}_s^a+\gamma \sum_{s^{\prime}\in S}\mathcal{P}_{SS^{\prime}}^av_\pi(s^{\prime}) qπ(s,a)=E[Rt+1+γqπ(St+1,At+1)∣St=s,At=a]=Rsa+γ∑s′∈SPSS′avπ(s′)






















 1023
1023











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








