损失函数——交叉熵损失函数_bp神经网络交叉熵loss曲线图-CSDN博客

本文链接：https://blog.csdn.net/weixin_44023658/article/details/107507506

交叉熵代价函数（Cross-entropy cost function）是用来衡量人工神经网络（ANN）的预测值与实际值的一种方式。与二次代价函数相比，它能更有效地促进ANN的训练。在介绍交叉熵代价函数之前，本文先简要介绍二次代价函数，以及其存在的不足。

一、二次代价函数的不足

ANN的设计目的之一是为了使机器可以像人一样学习知识。人在学习分析新事物时，当发现自己犯的错误越大时，改正的力度就越大。比如投篮：当运动员发现自己的投篮方向离正确方向越远，那么他调整的投篮角度就应该越大，篮球就更容易投进篮筐。同理，我们希望：ANN在训练时，如果预测值与实际值的误差越大，那么在反向传播训练的过程中，各种参数调整的幅度就要更大，从而使训练更快收敛。然而，如果使用二次代价函数训练ANN，看到的实际效果是，如果误差越大，参数调整的幅度可能更小，训练更缓慢。

以一个神经元的二类分类训练为例，进行两次实验（ANN常用的激活函数为sigmoid函数，该实验也采用该函数）：输入一个相同的样本数据x=1.0（该样本对应的实际分类y=0）；两次实验各自随机初始化参数，从而在各自的第一次前向传播后得到不同的输出值，形成不同的代价（误差）：

在这里插入图片描述

实验1：第一次输出值为0.82
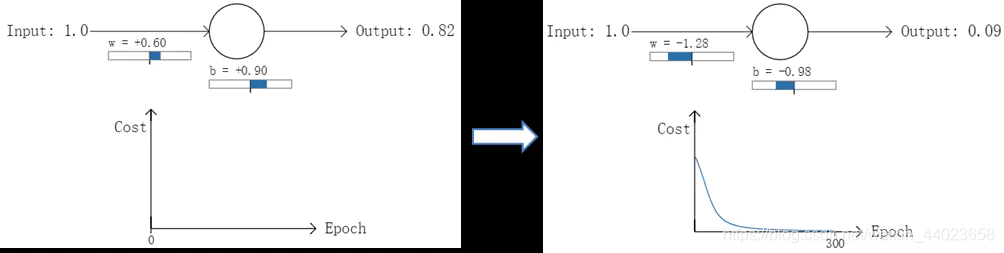
在这里插入图片描述

实验2：第一次输出值为0.98
在实验1中，随机初始化参数，使得第一次输出值为0.82（该样本对应的实际值为0）；经过300次迭代训练后，输出值由0.82降到0.09，逼近实际值。而在实验2中，第一次输出值为0.98，同样经过300迭代训练，输出值只降到了0.20。

从两次实验的代价曲线中可以看出：实验1的代价随着训练次数增加而快速降低，但实验2的代价在一开始下降得非常缓慢；直观上看，初始的误差越大，收敛得越缓慢。

其实，误差大导致训练缓慢的原因在于使用了二次代价函数。二次代价函数的公式如下：
$C=\frac{1}{2 n} \sum_{x}\left\|y(x)-a^{L}(x)\right\|^{2}$

其中，C表示代价，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。为简单起见，同样一个样本为例进行说明，此时二次代价函数为：
$C=\frac{(y-a)^{2}}{2}$
目前训练ANN最有效的算法是反向传播算法。简而言之，训练ANN就是通过反向传播代价，以减少代价为导向，调整参数。参数主要有：神经元之间的连接权重w，以及每个神经元本身的偏置b。调参的方式是采用梯度下降算法 ( Gradient descent )，沿着梯度方向调整参数大小。W和b的梯度推导如下：
$\begin{array}{l} \frac{\partial C}{\partial w}=(a-y) \sigma^{\prime}(z) x \\ \frac{\partial C}{\partial b}=(a-y) \sigma^{\prime}(z) \end{array}$

其中，Z表示神经元的输入，の表示激活函数。从以上公式可以看出，W和b的梯度跟激活函数的梯度成正比，激活函数的梯度越大，w和b的大小调整得越快，训练收合得就越快。而神经网络常用的激活函数为sigmoid函数，该函数的曲线如下所示：
在这里插入图片描述
如图所示，实验2的初始输出值（0.98）对应的梯度明显小于实验1的输出值（0.82），因此实验2的参数梯度下降得比实验1慢。这就是初始的代价（误差）越大，导致训练越慢的原因。与我们的期望不符，即：不能像人一样，错误越大，改正的幅度越大，从而学习得越快。

可能有人会说，那就选择一个梯度不变化或变化不明显的激活函数不就解决问题了吗？图样图森破，那样虽然简单粗暴地解决了这个问题，但可能会引起其他更多更麻烦的问题。而且，类似sigmoid这样的函数（比如tanh函数）有很多优点，非常适合用来做激活函数，具体请自行google之

交叉熵代价函数的定义

那么我们如何解决这个问题呢？研究表明, 我们可以通过使用交叉嫡函数来替换二次代价函数。为了理解什么是交叉嫡, 我们稍微改变一下之前的简单例子。假设, 我们现在要训练一个包含若干输
入变量的的神经元, $x_{1}, x_{2}, \ldots$ 对应的权重为 $w_{1}, w_{2}, \ldots$ 和偏置 $b$ :
在这里插入图片描述
神经元的输出就是 $a=\sigma(z),$ 其中 $z=\sum_{j} w_{j} x_{j}+b_{\text { } \text { }}$ 是输入的带权和。我们如下定义这个神经元的交叉嫡代价函数:
$C=-\frac{1}{n} \sum_{x}[y \ln a+(1-y) \ln (1-a)]$

其中 $n$ 是训练数据的总数，求和是在所有的训练输入 $x$ 上进行的， $y$ 是对应的目标输出。
对于交叉嫡代价函数, 针对一个训练样本 $x$ 的输出误差 $\delta^{L}$ 为
$\delta^{L}=a^{L}-y$
关于输出层的权重的偏导数为
$\frac{\partial C}{\partial w_{j k}^{L}}=\frac{1}{n} \sum_{x} a_{k}^{L-1}\left(a_{j}^{L}-y_{j}\right)$
这里 $\sigma^{\prime}\left(z_{j}^{L}\right)$ 就消失了，所以交叉嫡避免了学习缓慢的问题。

那么我们应该在什么时候用交叉熵来替换二次代价函数？实际上，如果在输出神经元是 $S$ 时，交叉熵一般都是更好的选择。为什么？考虑一下我们初始化网络的权重和偏置的时候通常使用某种随机方法。可能会发生这样的情况，这些初始选择会对某些训练输入误差相当明显，比如说，目标输出是 $1$ ，而实际值是 $0$ ，或者完全反过来。如果我们使用二次代价函数，那么这就会导致学习速度的下降。它并不会完全终止学习的过程，因为这些权重会持续从其他的样本中进行学习，但是显然这不是我们想要的效果。

交叉熵在分类问题中的应用

交叉熵损失函数应用在分类问题中时，不管是单分类还是多分类，类别的标签都只能是 0 或者 1。

交叉熵在单分类问题中的应用

这里的单类别是指，每一张图像样本只能有一个类别，比如只能是狗或只能是猫。交叉熵在单分类问题上基本是标配的方法

$\operatorname{los} s=-\sum_{i=1}^{n} y_{i} \log \left(\hat{y}_{i}\right)$
上式为一张样本的 loss 计算方法。式中 $n$ 代表着 $n$ 种类别。举例如下

$\begin{array}{|l|l|l|l|} \hline * & \text { 猫 } & \text { 青蛙 } & \text { 老鼠 } \\ \hline \text { Label } & 0 & 1 & 0 \\ \hline \text { Pred } & 0.3 & 0.6 & 0.1 \\ \hline \end{array}$

那么
$\begin{aligned} \operatorname{los} s &=-(0 \times \log (0.3)+1 \times \log (0.6)+0 \times \log (0.1)\\ &=-\log (0.6) \end{aligned}$
对应一个batch的loss就是
$\operatorname{los} s=-\frac{1}{m} \sum_{j=1}^{m} \sum_{i=1}^{n} y_{j i} \log \left(\hat{y}_{j i}\right)$
m为当前batch的样本数

交叉熵在多标签问题中的应用

这里的多类别是指，每一张图像样本可以有多个类别，比如同时包含一只猫和一只狗和单分类问题的标签不同，多分类的标签是n-hot。
$\begin{array}{|l|l|l|l|} \hline * & \text { 猫 } & \text { 青蛙 } & \text { 老鼠 } \\ \hline \text { Label } & 0 & 1 & 1 \\ \hline \text { Pred } & 0.1 & 0.7 & 0.8 \\ \hline \end{array}$

值得注意的是，这里的Pred采用的是sigmoid函数计算。将每一个节点的输出归一化到[0,1]之间。所有Pred值的和也不再为1。换句话说，就是每一个Label都是独立分布的，相互之间没有影响。所以交叉熵在这里是单独对每一个节点进行计算，每一个节点只有两种可能值，所以是一个二项分布。对于二项分布这种特殊的分布，熵的计算可以进行简化。

同样的，交叉熵的计算也可以简化，即
$\operatorname{loss}=-y \log (\hat{y})-(1-y) \log (1-\hat{y})$
注意，上式只是针对一个节点的计算公式。这一点一定要和单分类Ioss区分开来。
例子中可以计算为：
$\begin{array}{l} \operatorname{los} s_{\text {猫 }}=-0 \times \log (0.1)-(1-0) \log (1-0.1)=-\log (0.9) \\ \operatorname{los} s_{\text {蛙 }}=-1 \times \log (0.7)-(1-1) \log (1-0.7)=-\log (0.7) \\ \operatorname{los} s_{\text {鼠 }}=-1 \times \log (0.8)-(1-1) \log (1-0.8)=-\log (0.8) \end{array}$

单张样本的loss即为loss $s_{\text {猫 }}+\operatorname{loss} _{\text {娃 }}+\operatorname{loss} _{\text {氏 }}$ 每一个batch的loss就是：
$\operatorname{loss}=\sum_{j=1}^{m} \sum_{i=1}^{n}-y_{j i} \log \left(\hat{y}_{j i}\right)-\left(1-y_{j i}\right) \log \left(1-\hat{y}_{j i}\right)$
式中m为当前batch中的样本量，n为类别数。

交叉熵代价函数对权重求导的证明

交叉熵代价函数的定义：
$C=-\frac{1}{n} \sum_{x}[y \ln a+(1-y) \ln (1-a)]$
代价函数 $C$ 对 $w_{j k}^{L}$ 求偏导
$\begin{aligned} \frac{\partial C}{\partial w_{j k}^{L}} &=-\frac{1}{n} \sum_{x}\left(\frac{y_{j}^{L}}{\sigma\left(z_{j}^{L}\right)}-\frac{\left(1-y_{j}^{L}\right)}{1-\sigma\left(z_{j}^{L}\right)}\right) \frac{\partial \sigma\left(z_{j}^{L}\right)}{\partial w_{j k}^{L}} \\ &=-\frac{1}{n} \sum_{x}\left(\frac{y_{j}^{L}}{\sigma\left(z_{j}^{L}\right)}-\frac{\left(1-y_{j}^{L}\right)}{1-\sigma\left(z_{j}^{L}\right)}\right) \sigma^{\prime}\left(z_{j}^{L}\right) a_{k}^{L-1} \\ &=\frac{1}{n} \sum_{x} \frac{\sigma^{\prime}\left(z_{j}^{L}\right) a_{k}^{L-1}}{\sigma\left(z_{j}^{L}\right)\left(1-\sigma\left(z_{j}^{L}\right)\right)}\left(\sigma\left(z_{j}^{L}\right)-y_{j}\right) \end{aligned}$

其中 $\frac{\partial z_{j}^{l}}{\partial w_{j k}^{l}}=a_{k}^{l-1}$ 来自, 根据 $z_{j}^{l}$ 定义
$z_{j}^{l}=\sum_{k} w_{j k}^{l} a_{k}^{l-1}+b_{j}^{l}$
所以
$\frac{\partial z_{j}^{l}}{\partial w_{j k}^{l}}=a_{k}^{l-1}$
根据 $\sigma(z)=1 /\left(1+e^{-z}\right)$ 的定义

$\begin{aligned} \sigma^{\prime}(z) &=\left(\frac{1}{1+e^{-z}}\right)^{\prime} \\ &=\frac{e^{-z}}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{1+e^{-z}-1}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{1}{\left(1+e^{-z}\right)}\left(1-\frac{1}{\left(1+e^{-z}\right)}\right) \\ &=\sigma(z)(1-\sigma(z)) \end{aligned}$
把 $\sigma^{\prime}(z)$ 带入 $\frac{\partial C}{\partial w_{j}}$ 可街
$\frac{\partial C}{\partial w_{j k}^{L}}=\frac{1}{n} \sum_{x} a_{k}^{L-1}\left(a_{j}^{L}-y_{j}\right)$
其向量形式是
$\frac{\partial C}{\partial w^{L}}=\frac{1}{n} \sum_{x} a_{j}^{L-1}\left(\sigma\left(z^{L}\right)-y\right)$
对偏置用同样的方法可得
$\frac{\partial C}{\partial b_{j}^{L}}=\frac{1}{n} \sum_{x}\left(a_{j}^{L}-y_{j}\right)$

交叉熵的含义和来源

我们对于交叉熵的讨论聚焦在代数分析和代码实现。这虽然很有用，但是也留下了一个未能回答的更加宽泛的概念上的问题，如：交叉熵究竟表示什么？存在一些直觉上的思考交叉熵的方法吗？我们如何想到这个概念？

让我们从最后一个问题开始回答：什么能够激发我们想到交叉熵？假设我们发现学习速度下降了，并理解其原因是因为对于二次代价函数,输出层的权重的偏导数为

$\frac{\partial C}{\partial w_{j k}^{L}}=\frac{1}{n} \sum_{x} a_{k}^{L-1}\left(a_{j}^{L}-y_{j}\right) \sigma^{\prime}\left(z_{j}^{L}\right)$
项 $\sigma^{\prime}\left(z_{j}^{L}\right)$ 会在一个输出神经元困在错误值时导致学习速度的下降。在研究了这些公式后, 我们可能就会想到选择一个不包含 $\sigma^{\prime}(z)$ 的代价函数。所以, 这时候对一个训练样本 $x$ , 其代价 $C=C_{x}$ 满足:

$\begin{array}{c} \frac{\partial C}{\partial w_{j}}=a_{j}^{L-1}\left(a_{j}^{L}-y\right) \\ \frac{\partial C}{\partial b}=(a-y) \end{array}$
如果我们选择的损失函数满足这些条件，那么它们就能以简单的方式呈现这样的特性：初始误差越大，神经元学习得越快。这也能够解决学习速度下降的问题。实际上，从这些公式开始，现在我们就看看凭着我们数学的直觉推导出交叉熵的形式是可行的。我们来推一下，由链式法则，我们有

$\frac{\partial C}{\partial b}=\frac{\partial C}{\partial a} \sigma^{\prime}(z)$
使用 $\sigma^{\prime}(z)=\sigma(z)(1-\sigma(z))=a(1-a),$ 上个等式就变成
$\frac{\partial C}{\partial b}=\frac{\partial C}{\partial a} a(1-a)$
对比等式, 我们有
$\frac{\partial C}{\partial a}=\frac{a-y}{a(1-a)}$
对此方程关于 $a$ 进行积分, 得到
$\ln a+(1-y) \ln (1-a)]+\text { constant }$
其中 constant 是积分常量。这是一个单独的训练样本 $x$ 对损失函数的贡献。为了得到整个的损失函数, 我们需要对所有的训练样本进行平均, 得到了
$C=-\frac{1}{n} \sum_{x}[y \ln a+(1-y) \ln (1-a)]+\text { constant }$
而这里的常量就是所有单独的常量的平均。所以我们看到方程
$\begin{array}{c} \frac{\partial C}{\partial w_{j}}=a_{j}^{L-1}\left(a_{j}^{L}-y\right) \\ \frac{\partial C}{\partial b}=(a-y) \end{array}$
唯一确定了交叉嫡的形式，并加上了一个常量的项。这个交叉嫡并不是凭空产生的。而是一种我们以自然和简单的方法获得的结果。那么交叉嫡直觉含义又是什么？我们如何看待它？深入解释这一点会将我们带到一个不大愿意讨论的领域。然而，还是值得提一下，有一种源自信息论的解释交叉嫡的标准方式。粗略地说，交叉嫡是"不确定性"的一种度量。特别地, 我们的神经元想要计算函数 $x\rightarrow y=y(x)$ 。但是, 它用函数 $\rightarrow a=a(x)$ 进行了替换。假设我们将 $a$ 想象成我们神经元估计为 $y = 1$ 的概率, 而 $1 - a$ 则是 $y = 0$ 的概率。那么交叉嫡衡量我们学习到 $y$ 的正确值的平均起来的不确定性。如果输出我们期望的结果，不确定性就会小一点; 反之，不确定性就大一些。

当然，我这里没有严格地给出"不确定性"到底意味着什么，所以看起来像在夸夸其谈。但是实际上，在信息论中有一种准确的方式来定义不确定性究竟是什么。详细内容请看交叉嫡（cross-entropy）的数学历史。

交叉熵（cross-entropy）的数学历史

通用的说，熵(Entropy)被用于描述一个系统中的不确定性(the uncertainty of a system)。在不同领域熵有不同的解释，比如热力学的定义和信息论也不大相同。
先给出一个"不严谨"的概念表述：

熵：可以表示一个事件A的自信息量，也就是A包含多少信息。
KL散度：可以用来表示从事件A的角度来看，事件B有多大不同。
交叉熵：可以用来表示从事件A的角度来看，如何描述事件B。

一句话总结的话：KL散度可以被用于计算代价，而在特定情况下最小化KL散度等价于最小化交叉熵。而交叉熵的运算更简单，所以用交叉熵来当做代价。
信息量

首先是信息量。假设我们听到了两件事，分别如下：
事件A：巴西队进入了2018世界杯决赛圈。
事件B：中国队进入了2018世界杯决赛圈。

仅凭直觉来说，显而易见事件B的信息量比事件A的信息量要大。究其原因，是因为事件A发生的概率很大，事件B发生的概率很小。所以当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。

假设 $X$ 是一个离散型随机变量, 其取值集合为 $\chi$ ,概率分布函数 $p(x)=\operatorname{Pr}(X=x), x \in \chi$ 则定义事件 $X=x_{0}$ 的信息量为:
$I\left(x_{0}\right)=-\log \left(p\left(x_{0}\right)\right)$
由于是概率所以 $p\left(x_{0}\right)$ 的取值范围是[0, 1], 绘制为图形如下：
在这里插入图片描述
什么是熵(Entropy)？

放在信息论的语境里面来说，就是一个事件所包含的信息量。我们现在有了信息量的定义，而熵用来表示所有信息量的期望，即：
$\text { 因此嫡被定义为 } S(x)=-\sum_{i} P\left(x_{i}\right) \log _{b} P\left(x_{i}\right)$

如何衡量两个事件/分布之间的不同：KL散度

我们上面说的是对于一个随机变量x的事件A的自信息量，如果我们有另一个独立的随机变量x相关的事件B，该怎么计算它们之间的区别？
此处我们介绍默认的计算方法：KL散度，有时候也叫KL距离，一般被用于计算两个分布之间的不同。看名字似乎跟计算两个点之间的距离也很像，但实则不然，因为KL散度不具备有对称性。在距离上的对称性指的是A到B的距离等于B到A的距离。

KL散度的数学定义：

相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异
维基百科对相对熵的定义

In the context of machine learning, DKL(P‖Q) is often called the information gain achieved if P is used instead of Q.

对于离散事件我们可以定义事件A和B的差别为：

如果 $P_{A}=P_{B}$ , 即两个事件分布完全相同，那么KL散度等于0。
观察公式, 可以发现减号左边的就是事件A的嫡，请记住这个发现。
如果颠倒一下顺序求 $D_{K L}(B|| A),$ 那么就需要使用B的嫡，答案就不一样了。所以KL散度来计算两个分布A与B的时候是不是对称的，有"坐标系"的问题** $D_{K L}(A|| B) \neq D_{K L}(B|| A)$

换句话说，KL散度由A自己的熵与B在A上的期望共同决定。当使用KL散度来衡量两个事件(连续或离散)，上面的公式意义就是求 A与B之间的对数差在 A上的期望值。

KL散度 = 交叉熵 - 熵？

如果我们默认了用KL散度来计算两个分布间的不同，那还要交叉熵做什么？

事实上交叉嫡和KL散度的公式非常相近, 其实就是KL散度的后半部分(公式2.1)：A和B的交叉嫡 A与B的KL散度 - A的嫡。 $D_{K L}(A \| B)=-S(A)+H(A, B)$

对比一下这是KL散度的公式:

$D_{K L}(A|| B)=\sum_{i} P_{A}\left(x_{i}\right) \log \left(\frac{P_{A}\left(x_{i}\right)}{P_{B}\left(x_{i}\right)}\right)=\sum_{i} P_{A}\left(x_{i}\right) \log \left(P_{A}\left(x_{i}\right)\right)-P_{A}\left(x_{i}\right) \log \left(P_{B}\left(x_{i}\right)\right)$
这是嫡的公式：
$S(A)=-\sum_{i} P_{A}\left(x_{i}\right) \log P_{A}\left(x_{i}\right)$
这是交叉嫡公式:
$B)=-\sum_{i} P_{A}\left(x_{i}\right) \log \left(P_{B}\left(x_{i}\right)\right)$
此处最重要的观察是, 如果 $S (A)$ 是一个常量, 那么 $D_{K L}(A \| B)=H(A, B)$ , 也就是说 KL散度和交叉嫡在特定条件下等价。。

为什么交叉嫡可以用作代价？

接着上一点说，最小化模型分布 $P(\bmod e l)$ 与训练数据上的分布 $P(\text {training})$ 的差异等价于最小化这两个分布间的KL散度, 也就是最小化 $\| P(m o d e l))$
比照第四部分的公式：

此处的A就是数据的真实分布： $\quad P(\text { training })$
此处的B就是模型从训练数据上学到的分布： $\quad P(\text { model })$

巧的是，训练数据的分布A是给定的。那么根据我们在第四部分说的，因为A固定不变，那么求 $D_{K L}(A|| B)$ 等价于求 $H (A, B),$ 也就是A与B的交叉嫡。得证, 交叉嫡可以用于计算"学习模型的分布"与"训练数据分布"之间的不同。当交叉嫡最低时(等于训练数据分布的嫡)，我们学到了 '最好的模型"。