西北农林科技大学2020年算法分析与设计实验二——基于动态规划方法求解0-1背包等问题

最新推荐文章于 2022-10-29 10:52:57 发布

努力的算算

最新推荐文章于 2022-10-29 10:52:57 发布

阅读量2.7k

点赞数 5

分类专栏：算法文章标签：算法

本文链接：https://blog.csdn.net/weixin_44029810/article/details/110341052

版权

算法专栏收录该内容

4 篇文章 1 订阅

订阅专栏

实验二

基于动态规划方法求解0-1背包等问题

实验内容

本实验要求基于算法设计与分析的一般过程
（即待求解问题的描述、算法设计、算法描述、算法正确性证明、算法分析、算法实现与测试），在针对0-1背包问题求解的实践中理解动态规划 (Dynamic Programming, DP) 方法的思想、求解策略及步骤。
作为挑战：可以完成基于跳跃点的改进算法，以支持连续型物品重量/背包容量且提高算法的效率。

实验目的

理解动态规划方法的核心思想以及动态规划方法的求解过程；
从算法分析与设计的角度，对0-1背包问题的基于DP法求解有更进一步的理解。

环境要求

对于环境没有特别要求。对于算法实现，可以自由选择C, C++, Java，甚至于其他程序设计语言如Python等。

我选择c++语言作为此算法的实现语言

实验结果

步骤1：

理解问题，给出问题的描述。

n个物品和1个背包。对物品i，其价值为v_i，重量为w_i，背包容量为W。如何选取物品装入背包，使背包中所装入的物品的总价值最大？其中，w_i, W都是正整数。

给定一个背包，已知背包的最大承重为
packageWeight ，再给出若干件(numbers件)物品，已经每件物品的重量和对应的价值。

物品的重量存储在weight[]数组中，物品的价值存储在value[]数组中。

现在要求：应该挑选哪几件物品，使得背包装下最大的价值（P.S.：装的物品的重量不能超过背包的承重）

最后打印出了装入了哪几件物品
公式化描述为
给定C>0,w_i>0,v_i>0,1≤i≤n,要求找出n元0-1向量(x₁,x₂,x₃,……,x_n),1≤i≤n,使得 $\sum_{i=1}^n$ w_ix_i≤C,而且 $\sum_{i=1}^n$ w_ix_i≤C达到最大。

约束条件:
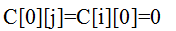
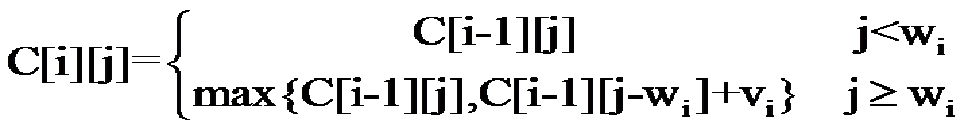
在这里插入图片描述

目标函数

max $\sum_{r=1}^n$ v_ix_i

步骤2

算法设计，包括策略与数据结构的选择

从规模最大的问题的最优解与其子问题的最优解的关系，一级一级抽象问题的一般表述，得出递归关系式：
在这里插入图片描述

包的容量比该商品体积小，装不下，此时的价值与此前i-1个的价值是一样的，即V(i,j)=V(i-1,j)
还有足够的容量装该商品，但装了也不一定达到当前最优价值，所以在装与不装之间选择最优的一个，即V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i))}

步骤3

描述算法。希望采用源代码以外的形式，如伪代码或流程图等

KNAPSACK-01-DP(w, v, W) //w为重量，v为价值，W为容量
  //C[1..n, 1..n]为最优值
  FOR i = 1 TO n
    C[i,0] = 0
  FOR j = 1 TO W
    C[0,j] = 0
  FOR i = 1 TO n
    FOR j = 1 TO W
      IF j < w[i]
        C[i,j] = C[i-1][j]
      ELSE
        C[i,j] = MAX{C[i-1][j],C[i-1][j-w[i] + v[i]}
  RETURN C

KNAPSACK-TRACEBACK-01(w,W,C,X) //w为重量，W为容量，C为最优值
  //X[1..n]为构建的最优解
  n = w.length – 1
  j = W //Remained Capacity
  FOR i = n TO 1
    IF C[i][j] == C[i-1][j]
      X[i] = 0
    ELSE
      X[i] = 1
      j -= w[i]
  RETURN X

在这里插入图片描述

步骤4

算法的正确性证明。需要这个环节，在理解的基础上对算法的正确性给予证明；此题目证明循环不变式,网络上的不变式理解循环不变式

步骤5

算法复杂性分析，包括时间复杂性和空间复杂性；时间复杂性：

O(n )

空间复杂性：

O(1)

步骤6

算法实现与测试。附上代码或以附件的形式提交，同时贴上算法运行结果截图;

#include <iostream>
#include <math.h>

int **knapack01DP(int *v, int *w, int multiWeight, int n, int **C);

//C存放最优解,w为重量，v为价值，W为容量
int max(int a, int b) {
    return (a > b) ? a : b;
}

//void traceback(int **C,int *w,int *x,int c);
int *knapack01traceback(int *w, int multiWeight, int **C, int *X, int n);

int main() {
    int multiWeight;
    std::cin >> multiWeight;
    int n;
    std::cin >> n;
    int **C = new int *[n + 1];
    for (int i = 0; i < n + 1; ++i) {
        C[i] = new int[multiWeight + 1];
    }

    for (int i = 0; i < n + 1; ++i) {
        for (int j = 0; j < multiWeight + 1; ++j) {
            C[i][j] = 0;
        }
    }
    int *value = new int[n];
    for (int i = 0; i < n; ++i) {
        value[i] = 0;
    }
    value[0] = 0;
    for (int i = 1; i < n + 1; ++i) {
        std::cin >> value[i];
    }
    int *weight = new int[n + 1];
    for (int i = 0; i < n + 1; ++i) {
        weight[i] = 0;
    }
    weight[0] = 0;
    for (int i = 1; i < n + 1; ++i) {
        std::cin >> weight[i];
    }
    int *X = new int[n + 1];
    X[0] = 0;
    for (int i = 1; i < n + 1; ++i) {
        X[i] = 0;
    }

    C = knapack01DP(value, weight, multiWeight, n, C);
    X = knapack01traceback(weight, multiWeight, C, X, n);

    for (int i = 0; i <= n; ++i) {
        for (int j = 0; j <= multiWeight; ++j) {
//            C[i][j] = 0;
            std::cout << C[i][j] << " ";

        }
        std::cout << std::endl;
    }

    std::cout << "{x1,x2,x3,x4,x5,......,xn} = ";
    for (int i = 1; i <= n; i++) {
        std::cout <<X[i] << " ";
    }
    std::cout << std::endl;
    return 0;
}

int **knapack01DP(int *v, int *w, int multiWeight, int n, int **C) {
//    int **C=new int*[n];
//    for (int i = 0; i < n; ++i) {
//        C[i] = new int[n];
//    }

    for (int i = 1; i <= n; ++i) {
        C[i][0] = 0;
    }
    for (int i = 1; i <= multiWeight; ++i) {
        C[0][i] = 0;

    }
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= multiWeight; ++j) {
            if (j < w[i])
                C[i][j] = C[i - 1][j];
            else
                C[i][j] = max(C[i - 1][j], C[i - 1][j - w[i]] + v[i]);
        }
    }
    return C;
}

int *knapack01traceback(int *w, int multiWeight, int **C, int *X, int n) {
    int j = multiWeight;//保存总重量

    for (int i = n; i >= 1; i--) {
        if (C[i][j] == C[i - 1][j])
            X[i] = 0;
        else {
            X[i] = 1;
            j -= w[i];
        }
    }
    return X;
}

在这里插入图片描述

算法改进

问题描述

算法存在的问题

假设物品的重量w_i(1≤i≤n)为整数：

如果wi(1≤i≤n)为连续型的实数，如何枚举？

该算法复杂性目前为O(nW)：

当背包容量W很大时，算法所需的计算时间较多。
若W>2n，算法复杂性则为O(n × 2ⁿ)。指数级

算法的改进

在这里插入图片描述

伪代码

希望采用源代码以外的形式，如伪代码或流程图等

KNAPSACK-01-OPT(w, v, W) //w为重量，v为价值，W为容量
  //p[1..n, 2]：存放指定i的跳跃点即(j,C[i][j])值对。q[1..n, 2]：如定义
  p[0] = {(0, 0)}
  FOR i = 1 to n
    q[i-1] = p[i-1] + (w[i],v[i])
    p[i] = p[i-1] ∪ q[i-1]
    PROCESS(p[i],W) //剔除受控/无效的跳跃点
  RETURN p
BACKTRACK-OPT(w, v, p, n) //w为重量，v为价值，p为跳跃点的值对
  //x[1..n]：存放问题的解
  j = MAX(p[n][0]); m = MAX(p[n][1])
  FOR i = n TO 1
    IF (j, m) == p[i-1] + (w[i],v[i]) //其中一个满足
      x[i] = 1; j = p[i-1][0]; m = p[i-1][1]
    ELSE
      x[i] = 0
  RETURN x

算法实现与测试

// 动态规划 背包问题 跳跃点优化
#include <iostream>
using namespace std;
template<class Type>
void Traceback(int n,Type w[],Type v[],Type **p,int *head,int x[])
{
    Type j = p[head[0]-1][0],m=p[head[0]-1][1];
    for(int i=1; i<=n; i++)
    {
        x[i]=0;
        for(int k=head[i+1]; k<=head[i]-1; k++)
        {
            if(p[k][0]+w[i]==j && p[k][1]+v[i]==m)
            {
                x[i]=1;
                j=p[k][0];
                m=p[k][1];
                break;
            }
        }
    }
}
template<class Type>
int Knapsack(int n,Type c,Type v[],Type w[],int **p,int x[])
{
    int *head = new int[n+2];
    head[n+1]=0;
    p[0][0]=0;
    p[0][1]=0;
    int left = 0,right = 0,next = 1;
    head[n]=1;
    for(int i=n; i>=1; i--)
    {
        int k = left;
        for(int j=left; j<=right; j++)
        {
            if(p[j][0]+w[i]>c) break;
            Type y = p[j][0] + w[i],m = p[j][1] + v[i];
            while(k<=right && p[k][0]<y)
            {
                p[next][0]=p[k][0];
                p[next++][1]=p[k++][1];
            }
            if(k<=right && p[k][0]==y)
            {
                if(m<p[k][1])
                {
                    m=p[k][1];
                }
                k++;
            }
            if(m>p[next-1][1])
            {
                p[next][0]=y;
                p[next++][1]=m;
            }
            while(k<=right && p[k][1]<=p[next-1][1])
            {
                k++;
            }
        }
        while(k<=right)
        {
            p[next][0]=p[k][0];
            p[next++][1]=p[k++][1];
        }
        left = right + 1;
        right = next - 1;
        head[i-1] = next;
    }
    Traceback(n,w,v,p,head,x);
    return p[next-1][1];
}
int main()
{
    int c;
    cout<<"请输入待装物品的数量: "<<endl;
    int N;
    cin>>N;
    int w[N+1];
    int v[N+1];
    cout<<"请输入各个物品的重量及其对应价值:"<<endl;
    for(int i=1; i<=N; i++)
    {
        cin>>w[i];
        cin>>v[i];
    }
    int x[N+1];
    cout<<"请输入背包最大载重量:"<<endl;
    cin>>c;
    int **p = new int *[50];
    for(int i=0; i<50; i++)
    {
        p[i] = new int[2];
    }
    cout<<"背包能装的最大价值为："<<Knapsack(N,c,v,w,p,x)<<endl;
    cout<<"背包装下的物品编号为："<<endl;
    for(int i=1; i<=N; i++)
    {
        if(x[i]==1)
        {
            cout<<i<<" ";
        }
    }
    cout<<endl;
    for(int i=0; i<50; i++)
    {
        delete p[i];
    }
    delete[] p;
    return 0;
}

在这里插入图片描述

算法复杂性分析，包括时间复杂性和空间复杂性

在这里插入图片描述

时间复杂性：

O(min(nW, 2ⁿ))

空间复杂性：

O(n)

实验总结

动态规划方法的实质是分治思想和解决冗余：

分治思想：将原问题分解为更小、更易求解的子问题，然后对子问题进行求解，并最终产生原问题的解。
解决冗余：求解过程中，所有子问题只求解一次并以表的方式保存，对于相同子问题并不重复求解而通过查表的方式获得。

动态规划的求解步骤：

分析最优解的性质，以刻画最优解的结构特征 ——— 考察是否适合采用动态规划方法，即是否具备最优子结构性质；
递归定义最优值（即建立递归公式或动态规划方程），包括停止条件（递归出口）和递归体；
以自底向上的方式计算出最优值，并记录相关信息。应充分利用子问题重叠性质；
最终构造出最优解。

备忘录方法为动态规划方法的变形： **相同点**： - 采用表格保存已解决的子问题的值，在下次需要时直接查表而无需重新计算；

不同点：

备忘录方法采用自顶向下的递归方式，而动态规划方法则采用自底向上的递归方式。
其控制结构与直接递归的控制结构相同，区别在于备忘录方法为每个已
解的子问题建立备忘录以备需要时看，避免了相同子问题的重复求

适用条件

任何思想方法都有一定的局限性，超出了特定条件，它就失去了作用。同样，动态规划也并不是万能的。适用动态规划的问题必须满足最优化原理和无后效性。

最优化原理（最优子结构性质）
最优化原理可这样阐述：一个最优化策略具有这样的性质，不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简而言之，一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
无后效性
将各阶段按照一定的次序排列好之后，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策，而只能通过当前的这个状态。换句话说，每个状态都是过去历史的一个完整总结。这就是无后向性，又称为无后效性。
子问题的重叠性
采用自底向上的递归方式。
其控制结构与直接递归的控制结构相同，区别在于备忘录方法为每个已
解的子问题建立备忘录以备需要时看，避免了相同子问题的重复求

适用条件

最优化原理（最优子结构性质）
最优化原理可这样阐述：一个最优化策略具有这样的性质，不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简而言之，一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
无后效性
将各阶段按照一定的次序排列好之后，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策，而只能通过当前的这个状态。换句话说，每个状态都是过去历史的一个完整总结。这就是无后向性，又称为无后效性。
子问题的重叠性
动态规划算法的关键在于解决冗余，这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术，它在实现的过程中，不得不存储产生过程中的各种状态，所以它的空间复杂度要大于其他的算法。选择动态规划算法是因为动态规划算法在空间上可以承受，而搜索算法在时间上却无法承受，所以我们舍空间而取时间。

努力的算算

关注

5
点赞
踩
45

收藏

觉得还不错? 一键收藏
打赏
1
评论
西北农林科技大学2020年算法分析与设计实验二——基于动态规划方法求解0-1背包等问题

实验二基于动态规划方法求解0-1背包等问题实验内容本实验要求基于算法设计与分析的一般过程（即待求解问题的描述、算法设计、算法描述、算法正确性证明、算法分析、算法实现与测试），在针对0-1背包问题求解的实践中理解动态规划 (Dynamic Programming, DP) 方法的思想、求解策略及步骤。作为挑战：可以完成基于跳跃点的改进算法，以支持连续型物品重量/背包容量且提高算法的效率。实验目的理解动态规划方法的核心思想以及动态规划方法的求解过程；从算法分析与设计的角度，对0-1背包问.
复制链接

扫一扫