【机器学习】笔记3：Perceptron 感知机

1. Reference

刘建平 Pinard
Hsuan-Tien Lin ,National Taiwan University
统计学习方法 李航
 

2. Concept

参考台湾大学林轩田老师 机器学习基石课程。

2.1 Basic Notations

• $H$: the set of candidate formulas.

• $D$: data $\Rightarrow$ training examples.

• $f$: $X\to Y$ , which is the unknown pattern to be learned $\iff$ target function.

• $g$: $X\to Y$ , which is ‘learned’ formula to be used)

• $A$: learning algorithm

  We want
  $A$ takes $D$ (given) and $H$ (suitable) to get $g(best)$.
  Learning Model = $A$ and $H$.==
   

2.2 Learning Model

3. Perceptron

3.1 What is Perceptron?

在机器学习中，perceptron是一种二元分类的线性分类模型，它可以决定输入是属于一个类（+1，记为正类）还是另一个类（-1，记为负类）。
以恋爱为例，你自己本身就是一个perceptron，根据自己的择偶准则，异性在你的眼里就自动被划分为鱼塘内和鱼塘外两种类型（太魔鬼…）。
我们用数学的语言来进行更为准确的表达，用threshold表示择偶的门槛分数，也叫做阈值，$\mathbf{x}$ $=(x_1,x_2,...,x_d)$表示boy or girl 的features，$\mathbf{w}$ $=(w_1,w_2,...,w_d)$表示每一个feature的权重。

approve \quad ${\sum }_{i=1}^d{w}_i{x}_i>threshold$
deny \qquad ${\sum }_{i=1}^d{w}_i{x}_i<threshold$

 
此处，为了简化起见，记 $h(\mathbf{x}$$)=sign(({\sum }_{i=1}^d{w}_i{x}_i)-threshold)=sign({\sum }_{i=0}^d{w}_i{x}_i)=sign({\mathbf{w}}^{\mathbf{T}}\mathbf{x})$，where $x_0=+1,w_0=-threshold$
其中，$sign$是示性函数，
若${\mathbf{w}}^{\mathbf{T}}\mathbf{x}$大于0，即 ${\sum }_{i=1}^d{w}_i{x}_i-threshold>0$, 也就是boy or girl 的得分大于阈值的时候，$sign=+1$，那他/她就被划进鱼塘；在小于零的时候，$sign=-1$，那就放生。
所以，我们的目标是，寻找一张合适的网，进行最佳的渔场管理。

 
 

3.2 Why Perceptron?

简单地解决分类问题
从两个角度来解释“简单”，一方面是训练数据应该是线性可分的，另一方面，我们的解决办法也很简单，就是找到一个超平面完全将其分割开来。
 
 

3.3 How Perceptron?

3.31 Sketch

Rule: improve it  based on mistakes.

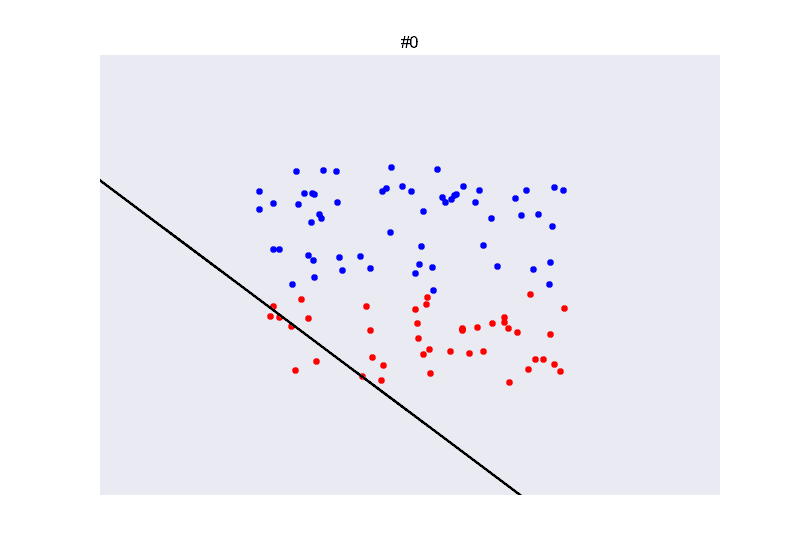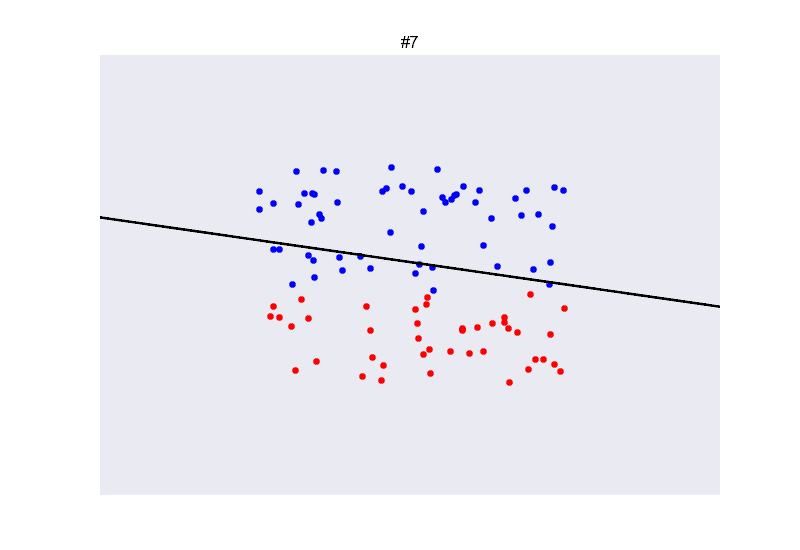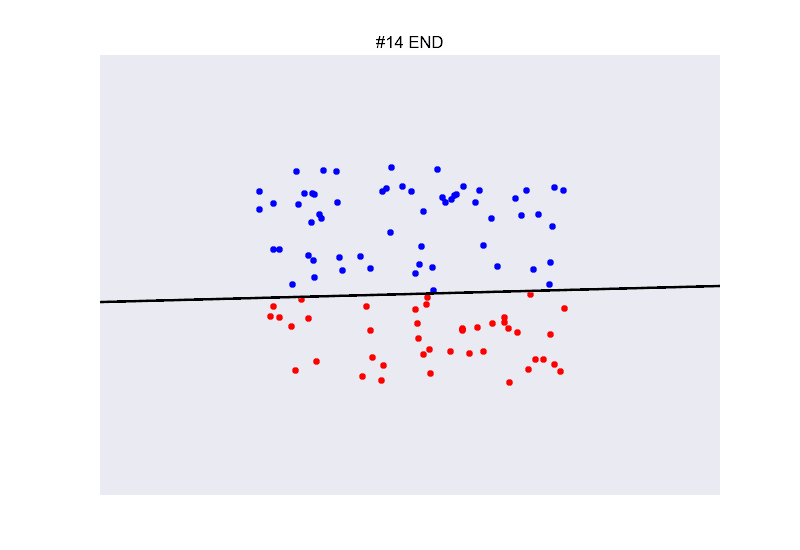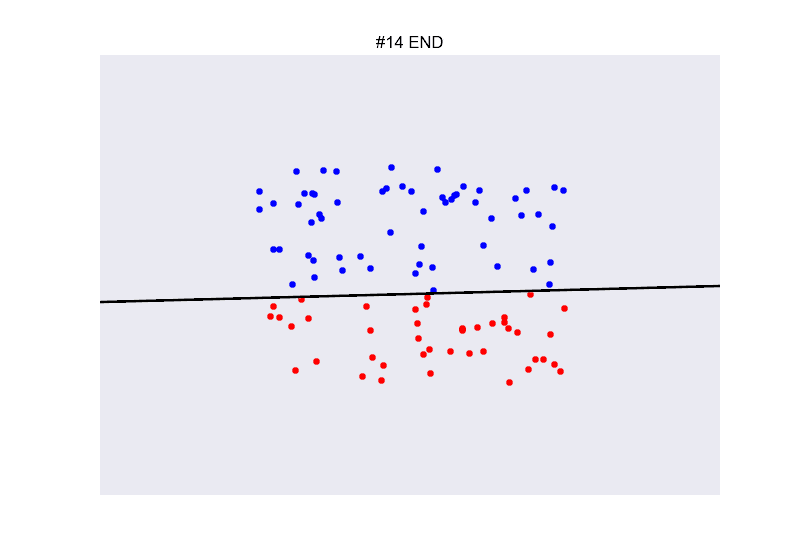
前文提到过，我们的目标是找到最佳的分类器，可以将训练集中的两类数据分开。
观察之前的数学式子，$sign({\mathbf{w}}^{\mathbf{T}}\mathbf{x})$的结果关乎判断对错，其中，用于训练的样本$\mathbf{x}$是给定的，无法改变，可以进行改动的就只有$\mathbf{w}$。所以，我们用$\mathbf{w}$来代表分类器。

为了更形象地进行说明，依旧以二维平面为例：上图中的黑色直线代表分类器，$\mathbf{w}$是其法向量。当选取了最优的$\mathbf{w}$时，分割线也就可以被唯一地表达出来，就是我们要找的分类器。所以，寻找最佳分类器的任务就是寻找最佳$\mathbf{w}$啦~~~
然而，在一般情况下，我们不可能一次就得到这样的分类器，可以完美地将两类数据分开。一开始，分类器可能会出现误分类的现象，基于它犯的这些错误，我们可以来一步步改进我们的分类器。
如下流程图所示，每当遇到分类错误的情况，我们就更新一次参数$\mathbf{w}$。

步骤：

1. 随机选取一个${\mathbf{w}}_{\mathbf{t}=0}$。（实际上，并没有那么“随便”。如果一开始选的分类器就不会“犯错”，那么后面的优化迭代也就无法进行。）
2. 随机选择样本点，如果样本点在该分类器下是正确分类的，则继续sample，直到发生第一次错误。（这里应该不是从全局的误分类点中随机抽样，点到即止可以提高运算效率）。
3. 修正$\mathbf{w}$。
4. 重复步骤2-3，如果某个分类器遍历所有样本都没有发生误分类的错误，则停止。

 
 

3.32 Details

3.321 Correction

可以看出，根据“误分类的样本点”来修正我们的分类器是关键所在。那么，具体又是如何进行修正的呢？

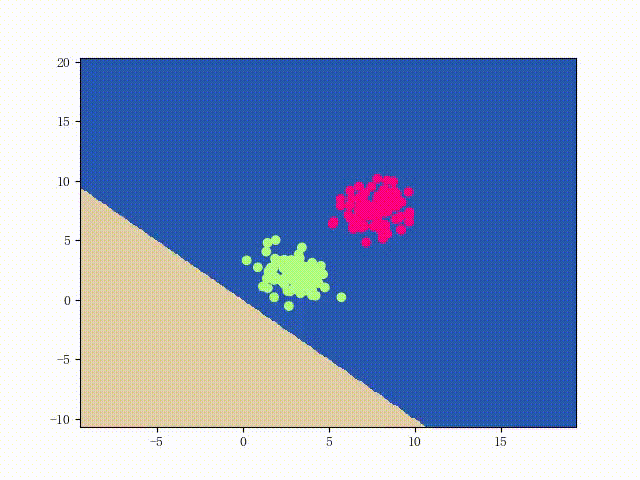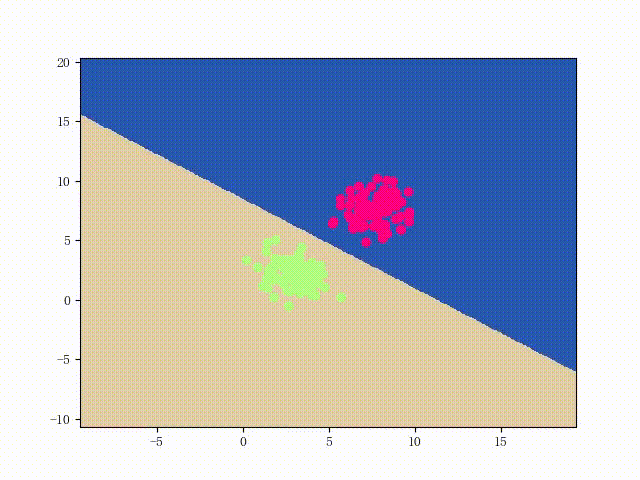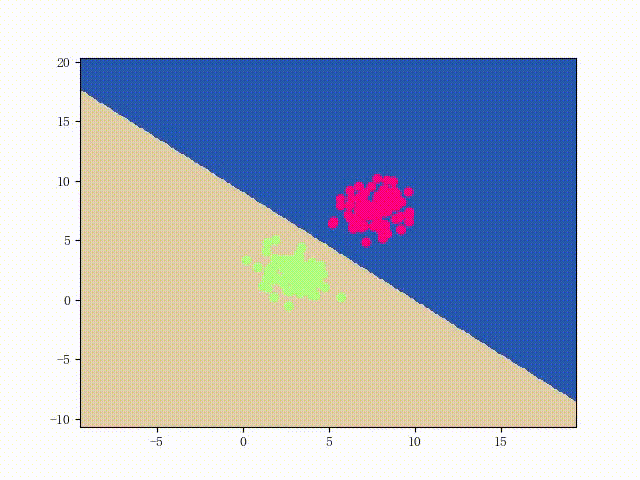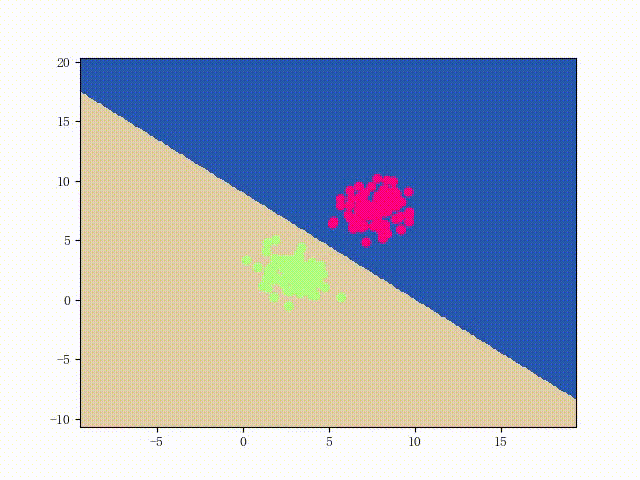
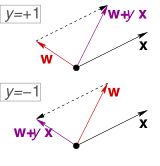
如下图所示，我们用具体的例子进行说明。其中，
$O$表示原点，
蓝色的点表示正类样本（+1），
红色的叉叉表示负类样本（-1）；
紫色的向量是法向量，与法向量垂直的灰色直线代表对应的分隔线。
我们可以清楚地观察到，样本点B和样本点C被分类错误了。

用数学形式表达如下：
$sign({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{B}}$)=$-1$, $y_B=+1$,
$sign({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{C}}$)=$+1$, $y_C=-1$.

对于正类样本点B来说，超平面的法向量$w$与其($\mathbf{x}$) 夹角却大于90°，所以产生误分类。那我们很自然的一个想法就是，根据这个“犯错点”来修正法向量，考虑${\mathbf{w}}_{\mathbf{t}+1}\leftarrow {\mathbf{w}}_{\mathbf{t}}$+$y_{n(t)}$${\mathbf{x}}_{\mathbf{n}(\mathbf{t})}$，即 ${\mathbf{w}}_{\mathbf{t}+1}={\mathbf{w}}_{\mathbf{t}}+{\mathbf{x}}_{\mathbf{B}}$.
同时，对于C点来说，超平面的法向量$w$与其($\mathbf{x}$) 夹角小于90°，所以产生误分类，那我们把$\mathbf{w}$朝着$\mathbf{x}$的反方向调节移动, 即${\mathbf{w}}_{\mathbf{t}+1}={\mathbf{w}}_{\mathbf{t}}-{\mathbf{x}}_{\mathbf{C}}$.
${\mathbf{w}}_{\mathbf{t}+1}={\mathbf{w}}_{\mathbf{t}}+{\mathbf{x}}_{\mathbf{B}}$ 和 ${\mathbf{w}}_{\mathbf{t}+1}={\mathbf{w}}_{\mathbf{t}}-{\mathbf{x}}_{\mathbf{C}}$可以被合并表示为${\mathbf{w}}_{\mathbf{t}+1}={\mathbf{w}}_{\mathbf{t}}$$+y_{n(t)}$${\mathbf{x}}_{\mathbf{n}(\mathbf{t})}$

我们以更严谨的形式描述PLA算法：

For $t=0,1,...$

1. find a mistake of ${\mathbf{w}}_{\mathbf{t}}$ called $({\mathbf{x}}_{\mathbf{n}(\mathbf{t})}$,$y_{n(t)})$
   $sign({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{n}(\mathbf{t})})$$=y_{n(t)}$
2. ( try to ) correct the mistake by
   ${\mathbf{w}}_{\mathbf{t}+1}\leftarrow {\mathbf{w}}_{\mathbf{t}}$+$y_{n(t)}$${\mathbf{x}}_{\mathbf{n}(\mathbf{t})}$

Until no more mistakes,
return last $\mathbf{w}$ (called ${\mathbf{w}}_{\mathbf{P}\mathbf{L}\mathbf{A}}$ ) as $g$

这里，我们需要特别注意，PLA存在许多解集，也就是说，不只存在一个超平面可以将两类数据完全分开。在进行PLA的过程中，我们可能每次会得到不同的结果，这些结果不仅依赖于我们对于${\mathbf{w}}_0$的选择，而且也依赖于迭代过程中对于误分类点的选择顺序。
 

让我们再回顾一下这张图，记紫色向量为${\mathbf{w}}_{\mathbf{t}}$,当我们选择点B对${\mathbf{w}}_{\mathbf{t}}$进行更新时,新的法向量为${\mathbf{w}}_{(\mathbf{t}+1)\mathbf{g}\mathbf{r}\mathbf{e}\mathbf{e}\mathbf{n}}$；然而，若我们选择了点C时，更新后的法向量为${\mathbf{w}}_{(\mathbf{t}+1)\mathbf{y}\mathbf{e}\mathbf{l}\mathbf{l}\mathbf{o}\mathbf{w}}$.

 

3.322 Break Point

因为数据是线性可分的，我们知道一定可以找到一个线性分类器将两类数据分开，也就是说，迭代一定是会停止的。那么问题在于，迭代的次数一定是有限的吗？
我们可以证明迭代次数一定是有限的。

MATH WARNING （T-T）

1. ${\mathbf{w}}_{\mathbf{t}+1}={\mathbf{w}}_{\mathbf{t}}$$+y_{n(t)}$${\mathbf{x}}_{\mathbf{n}(\mathbf{t})}$ (Correction)

2. ${\mathbf{y}}_{\mathbf{n}(\mathbf{t}+1)}{\mathbf{w}}_{\mathbf{f}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{n}}\ge$ $\underset{n}{\min }{\mathbf{y}}_{\mathbf{n}(\mathbf{t})}{\mathbf{w}}_{\mathbf{f}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{n}}$ (图中任意点在法向量上的投影长度都大于点T在其上的投影长度。)
   

3. ${\mathbf{w}}_{\mathbf{f}}^{\mathbf{T}}{\mathbf{w}}_{\mathbf{t}+1}\ge {\mathbf{w}}_{\mathbf{f}}^{\mathbf{T}}{\mathbf{w}}_{\mathbf{t}}+\underset{\mathbf{n}}{\min }{\mathbf{y}}_{\mathbf{n}(\mathbf{t})}{\mathbf{w}}_{\mathbf{f}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{n}}$

4. $\Vert {\mathbf{w}}_{\mathbf{t}+1}{\Vert }^2\le \Vert {\mathbf{w}}_{\mathbf{t}}{\Vert }^2+\underset{\mathbf{n}}{\max }\Vert {\mathbf{y}}_{\mathbf{n}}{\mathbf{x}}_{\mathbf{n}}{\Vert }^2$

5. ${\mathbf{w}}_{\mathbf{f}}^{\mathbf{T}}{\mathbf{w}}_{\mathbf{t}+1}\ge {\mathbf{w}}_{\mathbf{f}}^{\mathbf{T}}{\mathbf{w}}_0+(\mathbf{t}+1)\underset{\mathbf{n}}{\min }{\mathbf{y}}_{\mathbf{n}(\mathbf{t})}{\mathbf{w}}_{\mathbf{f}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{n}}$ (由3可得)

6. $\Vert {\mathbf{w}}_{\mathbf{t}+1}{\Vert }^2\le \Vert {\mathbf{w}}_0{\Vert }^2+(\mathbf{t}+1)\underset{\mathbf{n}}{\max }\Vert {\mathbf{y}}_{\mathbf{n}}{\mathbf{x}}_{\mathbf{n}}{\Vert }^2$ （由4可得）

7. $\frac{{\mathbf{w}}_{\mathbf{f}}^{{}^{\prime }}}{\Vert {\mathbf{w}}_{\mathbf{f}}\Vert }\frac{{\mathbf{w}}_{\mathbf{T}}}{\Vert {\mathbf{w}}_{\mathbf{T}}\Vert }=\mathbf{c}\mathbf{o}\mathbf{s}\theta \le 1$

8. $R^2=\underset{n}{\max }\Vert {\mathbf{x}}_{\mathbf{n}}{\Vert }^2$

9. $\rho =\underset{n}{\min }{\mathbf{y}}_{\mathbf{n}}\frac{{\mathbf{w}}_{\mathbf{f}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{n}}}{\Vert {\mathbf{w}}_{\mathbf{f}}\Vert }$
    

Finally, we get
$$\frac{{\mathbf{w}}_{\mathbf{f}}^{{}^{\prime }}}{\Vert {\mathbf{w}}_{\mathbf{f}}\Vert }\frac{{\mathbf{w}}_{\mathbf{T}}}{\Vert {\mathbf{w}}_{\mathbf{T}}\Vert }=\frac{1}{\Vert {\mathbf{w}}_{\mathbf{f}}^{{}^{\prime }}\Vert }\frac{\mathbf{T}\underset{\mathbf{n}}{\min }{\mathbf{y}}_{\mathbf{n}}{\mathbf{w}}_{\mathbf{f}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{n}}}{\sqrt{\mathbf{T}\ast \underset{\mathbf{n}}{\max }\Vert {\mathbf{x}}_{\mathbf{n}}{\Vert }^2}}=\sqrt{\mathbf{T}}\frac{\rho }{\mathbf{R}}$$

$$⟹T\le \frac{R^2}{{\rho }^2}$$

Oooooops!!!
 
 

3.4 统计学习角度

根据李航老师的统计计算一书，将统计学习方法解构为模型，策略和算法三个要素。

模型： 示性(符号)函数
$$f(x)=sign(wx+b)$$
$$sign(w^{T}x+b)=\{\begin{array}{rcl}+1& & w^{T}x+b\ge 0\\ -1& & w^{T}x+b<0\end{array}$$

 

策略：最小化误分类点到超平面的距离

$$min-\frac{1}{||w||}\sum _{x_i\in 误分类}{y}_i(w^T{x}_i+b)$$
 

算法： 随机梯度下降

  对损失函数求偏导得到其梯度，从而对$w,b$进行更新：

$${▽}_{w}L(w,b)=-\sum _{x_i\in 误分类}{y}_i{x}_i$$
$${▽}_{b}L(w,b)=-\sum _{x_i\in 误分类}{y}_i$$

  随机选择误分类点$(x_i,y_i)$,对$w,b$进行更新：
$$w_{new}\leftarrow w_{old}+y_i{x}_i$$

$$b_{new}\leftarrow b_{old}+y_i$$

 

3.5 To Be Continued…

3.51 Pocket

If noise in the data？
好了，至此PLA告一段落。
在现实生活中，两类数据完全线性可分的这种情况其实是比较少见的。如下图所示，两类数据并不能被直线完全分割开来。
我们考虑，那找一条犯错误最少的线好了！同时，因为数据线性不可分的原因，迭代不会停止，需要设置一个固定的迭代次数。
换句话说，我们每次更新参数的时候，都把之前的${\mathbf{w}}_{\mathbf{t}}$存储下来，当我们的口袋里装了足够多的分类器之后，最后从中选取一个犯错最少的分类器。

WARNING:
听起来，我们的算法好像变得更加实用了些。然而，每一次都要储存新的参数，也就意味着运算速度会降低。
如果数据的真实分布是线性可分的，口袋算法的效率可能还不如原始PLA高。

 
 

3.52 SVM

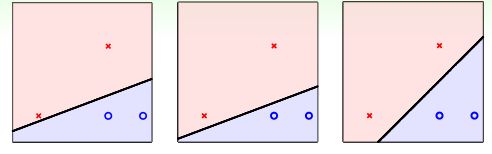
自始至终，我们的目标都是：找到一个超平面，将两类数据分开。可是，PLA的结果并不唯一。下图的三个超平面都可以将两类数据完美地分开，PLA 并不能帮助我们进行最优的选择。
直觉告诉我们，最右的分割线应该是最棒的。这就要提到SVM了，后面会详细介绍…