二叉排序树的定义及基本操作（构造、查找、插入、删除）递归及非递归算法

最新推荐文章于 2024-03-25 18:55:55 发布
最新推荐文章于 2024-03-25 18:55:55 发布
阅读量4w 收藏 811
点赞数 124
分类专栏： 经典编程题——二叉树与树 文章标签： c++ 二叉排序树 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_44162361/article/details/119112155
版权

文章目录

二叉排序树的定义

二叉排序树（Binary Sort Tree， BST），也称二叉查找树。
二叉排序树或者是一棵空树，或者是一棵具有下列特性的非空二叉树：
1） 若左子树非空，则左子树上所有结点关键字均小于根结点的关键字值；
2） 若右子树非空，则右子树上所有结点关键字均大于根结点的关键字值；
3） 左、右子树本身也分别是一棵二叉排序树。

由定义可知，二叉排序树是一个递归的数据结构，可以方便的使用递归算法对二叉排序树进行各种运算。
根据二叉树的定义，可得左子树结点值 ＜ 根结点值 ＜ 右子树结点值。
所以，对二叉排序树进行中序遍历，可以得到一个递增的有序序列。

二叉排序树的结点定义：

typedef struct BSTNode{
    int data;
    struct BSTNode *left;
    struct BSTNode *right;
}BSTNode;

二叉树结点的创建：

//二叉树结点创建
BSTNode *CreateTreeNode(int x){
    BSTNode *p = (BSTNode *)malloc(sizeof(BSTNode));
    p->data = x;
    p->left = NULL;
    p->right = NULL;
    return p;
}

二叉排序树的查找

 二叉排序树的查找是从根结点开始的，沿某个分支逐层向下进行比较的过程。
 其查找过程描述如下：若二叉排序树非空，则将给定值与根结点的关键字比较，若相等，则查找成功；若不等，则当根结点的关键字值大于给定关键字值时，在根结点的左子树中查找；否则在根结点的右子树中查找。

实现代码：

//查找的递归算法
BSTNode *Search(BSTNode *root, int x){
    if(root->data == x){
        return root;
    }else if(x < root->data){
        return Search(root->left, x);
    }else{
        return Search(root->right, x);
    }
}

//查找的非递归算法
BSTNode *Search(BSTNode *root, int x){
    BSTNode *p = root;
    while(p!=NULL && p->data!=x){
        if(x < p->data)
            p = p->left;
        else
            p = p->right;
    }
    return p;
}

二叉排序树的插入

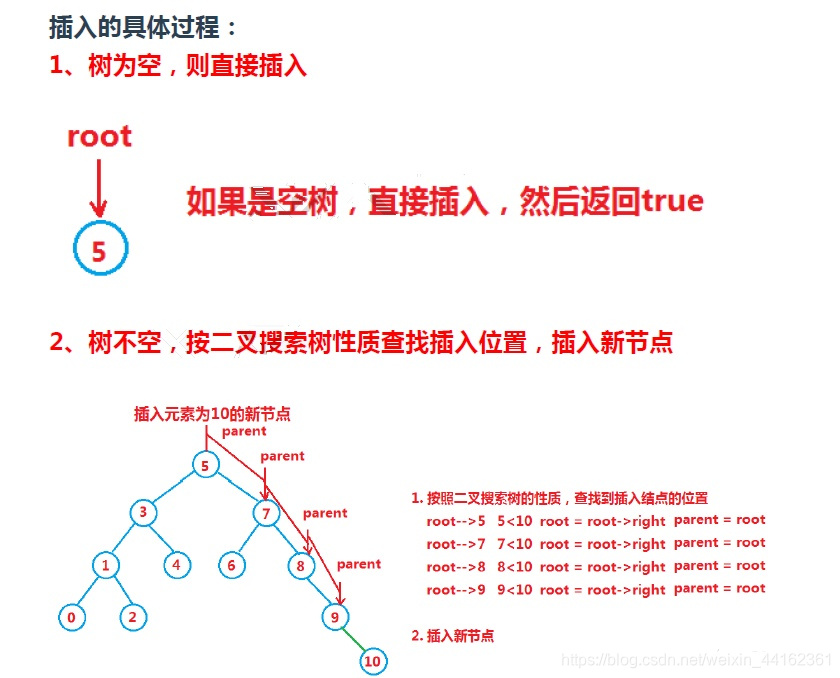
 二叉排序树作为一种动态集合，其特点是树的结构通常不是一次生成的，而是在查找过程中，当树中不存在关键字等于给定值的结点时再进行插入的。
 由于二叉排序树是递归定义的，因此插入结点的过程如下：若原二叉排序树为空，则直接插入结点；否则，若关键字＜根结点关键字，则插入左子树，若关键字＞根结点关键字，则插入右子树。

实现代码：

//插入的递归算法
BSTNode *Insert(BSTNode *root, int x){
    if(root == NULL){
        root = CreateTreeNode(x);
        return root;
    }
    if(x < root->data){
        root->left = Insert(root->left, x);
    }
    if(x > root->data){
        root->right = Insert(root->right, x);
    }
    return root;
}

请添加图片描述

//插入的非递归算法
BSTNode *Insert1(BSTNode *root, int x){
    BSTNode *parent = NULL;
    BSTNode *p = root;
    if(root == NULL){
        root = CreateTreeNode(x);
        return root;
    }
    while(p != NULL){
        parent = p;
        if(x < p->data){
            p = p->left;
        }else{
            p = p->right;
        }
    }
    if(parent->data >x){
        parent->left = CreateTreeNode(x);
    }else{
        parent->right = CreateTreeNode(x);
    }
    return root;
}

二叉排序树的构造

 构造一棵二叉排序树就是依次输入数据元素，并将它们插入二叉排序树中适当位置上的过程。
 构造二叉排序树的过程：每读入一个元素，就建立一个新结点，若二叉排序树为空，则将新结点作为二叉排序树的根结点；若二叉排序树非空，则将新结点的值与根结点的值比较，若小于根结点的值，则插入左子树，否则插入右子树。

实现代码：

void Create(BSTNode *&root, int str[], int n){
    root = NULL;
    for(int i=0; i<n; i++){
        Insert(root, str[i]);
    }
}

二叉排序树的删除

 在二叉排序树中删除一个结点时，不能把以该结点为根的子树上的结点都删除，必须先把被删除结点从存储二叉排序树的链表上摘下来，将因删除结点而断开的二叉链表重新链接起来，同时**确保二叉排序树的性质（左子树结点值＜根结点值＜右子树结点值）**不会丢失。

 删除操作一般会出现三种情况：
1） 若被删除结点z是叶结点，则直接删除，不会破坏二叉排序树的性质。
2） 若结点z只有一棵左子树或右子树，则让z的子树成为z父结点的子树，替代z的位置。
3） 若结点z有左、右两棵子树，则令z的直接后继（或直接前驱）替代z，然后从二叉排序树中删除这个直接后继（或直接前驱），这样就转换成了第一或第二种情况。

 注：已知二叉排序树经过中序遍历可以得到一个递增的有序序列，这里的直接后继（或直接前驱）应该是指被删除结点在这个中序遍历序列中的直接后继（或直接前驱）。
 
 体现在二叉排序树的图中:
 某个结点的直接后继为以该结点为根的右子树中最左下位置的结点，即右子树的最小值；
 某个结点的直接前驱为以该结点为根的左子树中最右下位置的结点，即左子树的最大值。

下面依次给出以上三种情况的实例及删除操作：
<1> 被删除结点是叶结点，如删除关键字为23的叶子结点。
在这里插入图片描述

<2.1>被删除结点z只有一棵左子树，删除关键字为45的结点。
在这里插入图片描述

<2.2>被删除结点z只有一棵右子树，如删除关键字为78的结点。
在这里插入图片描述

<3>被删除结点z有左、右两棵子树，如删除结点78。
 再强调一下寻找替代被删除结点的结点的原则以供结合下图思考：

 已知二叉排序树经过中序遍历可以得到一个递增的有序序列，这里的直接后继（或直接前驱）应该是指被删除结点在这个中序遍历序列中的直接后继（或直接前驱）。
 
 体现在二叉排序树的图中:
 某个结点的直接后继为以该结点为根的右子树中最左下位置的结点，即右子树的最小值；
 某个结点的直接前驱为以该结点为根的左子树中最右下位置的结点，即左子树的最大值。

在这里插入图片描述


实现代码：

//删除
bool Delete(BSTNode *p){
    //在二叉排序树中删除结点p, 并重新连接它的左右子树
    BSTNode *q, *s;
    //1.p为叶子结点
    if(p->left==NULL && p->right==NULL){
        p = NULL;
    }
    //2.1 p左子树为空, 重接右子树
    else if(p->left == NULL){
        q = p;
        p = p->right;
        free(q);
    }
    //2.2 p右子树为空, 重接左子树
    else if(p->right == NULL){
        q = p;
        p = p->left;
        free(q);
    }
    //3. p左右子树均不为空
    else{
        q = p;
        s = p->right; //找到p的右子树的最左端（中序直接后继）
        while(s->left != NULL){
            q = s;
            s = s->left;
        }
        p->data = s->data;
        
        if(q != p) //判断是否执行上述while循环
            q->left = s->right; //执行上述while循环，重接*q的左子树
        else
            q->right = s->right; //未执行上述while循环，重接*q的右子树，对于这个情况，可以参考代码后给出的示例图
        free(s);
    }
    return true;
}
bool DeleteBST(BSTNode *root, int x){
    if(root == NULL){
        return false;
    }else{
        if(x == root->data)
            return Delete(root); 
        else if(x < root->data)
            return DeleteBST(root->left, x);
        else
            return DeleteBST(root->right, x);
    }
}

对于未执行while循环的情况，如下图示例。
即未执行while循环的的情况为以被删除结点的右子树为根的树没有左子树只有右子树，也就是说，该右子树的最小值即为该根结点的值。
在这里插入图片描述

此外，在上面的代码中，在情况3中选择的是用被删除结点z的直接后继替代z，当然也可以用被删除结点z的直接前驱来替代，那么则需要修改为如下的代码即可。

//3. p左右子树均不为空
    else{
        q = p;
        s = p->left; //找到p的左子树的最右端（中序直接前驱）
        while(s->right != NULL){
            q = s;
            s = s->right;
        }
        p->data = s->data;
        
        if(q != p) //判断是否执行上述while循环
            q->right = s->left; //执行上述while循环，重接*q的右子树
        else
            q->left = s->left; //未执行上述while循环，重接*q的左子树
        free(s);
    }

完整代码及实例

#include<bits/stdc++.h>
using namespace std;

typedef struct BSTNode{
    int data;
    struct BSTNode *left;
    struct BSTNode *right;
}BSTNode;

#define N 100 

//查找的递归算法
BSTNode *Search(BSTNode *root, int x){
    if(root->data == x){
        return root;
    }else if(x < root->data){
        return Search(root->left, x);
    }else{
        return Search(root->right, x);
    }
}
//查找的非递归算法
BSTNode *Search1(BSTNode *root, int x){
    BSTNode *p = root;
    while(p!=NULL && p->data!=x){
        if(x < p->data)
            p = p->left;
        else
            p = p->right;
    }
    return p;
}

//二叉树结点创建
BSTNode *CreateTreeNode(int x){
    BSTNode *p = (BSTNode *)malloc(sizeof(BSTNode));
    p->data = x;
    p->left = NULL;
    p->right = NULL;
    return p;
}

//插入的递归算法
BSTNode *Insert(BSTNode *root, int x){
    if(root == NULL){
        root = CreateTreeNode(x);
        return root;
    }
    if(x < root->data){
        root->left = Insert(root->left, x);
    }
    if(x > root->data){
        root->right = Insert(root->right, x);
    }
    return root;
}
//插入的非递归算法
BSTNode *Insert1(BSTNode *root, int x){
    BSTNode *parent = NULL; //记录当前结点的父结点
    BSTNode *p = root;
    if(root == NULL){
        root = CreateTreeNode(x);
        return root;
    }
    while(p != NULL){
        parent = p;
        if(x < p->data){
            p = p->left;
        }else{
            p = p->right;
        }
    }
    if(parent->data >x){
        parent->left = CreateTreeNode(x);
    }else if(parent->data < x){
        parent->right = CreateTreeNode(x);
    }
    return root;
}


//构建
void Create(BSTNode *&root, int str[], int n){
    root = NULL;
    for(int i=0; i<n; i++){
        root = Insert(root, str[i]);
    }
}

//删除
bool Delete(BSTNode *p){
    //在二叉排序树中删除结点p, 并重新连接它的左右子树
    BSTNode *q, *s;
    //1.p为叶子结点
    if(p->left==NULL && p->right==NULL){
        p = NULL;
    }
    //2.1 p左子树为空, 重接右子树
    else if(p->left == NULL){
        q = p;
        p = p->right;
        free(q);
    }
    //2.2 p右子树为空, 重接左子树
    else if(p->right == NULL){
        q = p;
        p = p->left;
        free(q);
    }
    //3. p左右子树均不为空
    else{
        q = p;
        s = p->right; //找到p的右子树的最左端（中序直接后继）
        while(s->left != NULL){
            q = s;
            s = s->left;
        }
        p->data = s->data;
        
        if(q != p) //判断是否执行上述while循环
            q->left = s->right; //执行上述while循环，重接*q的左子树
        else
            q->right = s->right; //未执行上述while循环，重接*q的右子树
        free(s);
    }
    return true;
}
bool DeleteBST(BSTNode *root, int x){
    if(root == NULL){
        return false;
    }else{
        if(x == root->data)
            return Delete(root); 
        else if(x < root->data)
            return DeleteBST(root->left, x);
        else
            return DeleteBST(root->right, x);
    }
}


void LevelOrder(BSTNode *root){
    queue<BSTNode *> treenode; //队列存储结点
    if(root != NULL)
        treenode.push(root); //根结点入队
    while(!treenode.empty()){
        BSTNode *p = treenode.front(); 
        treenode.pop(); //根结点出队
        cout<<p->data<<" "; //输出队首元素，即当前访问的结点值
        if(p->left != NULL){
            treenode.push(p->left);//如果有左子树，则将左子树的根结点入队
        }
        if(p->right != NULL){
            treenode.push(p->right);//如果有右子树，则将右子树的根结点入队
        }
    }
}

int main(){
    BSTNode *root;
    int n;
    cin>>n;
    int str[n];
    for(int i=0; i<n; i++){
        cin>>str[i];
    }
    Create(root,str,n); 
    cout<<"当前二叉排序树的层序遍历序列为：";
    LevelOrder(root);
    cout<<endl;
    BSTNode *p = Search(root, 17);
    cout<<"结点17的右孩子结点值为："<<p->right->data<<endl;
    DeleteBST(root, 78);
    cout<<"删除结点78后的二叉排序树的层序遍历序列为：";
    LevelOrder(root);
    return 0;
}

构建的二叉排序树如下图所示，删除时为删除结点78.
在这里插入图片描述

运行结果为：
在这里插入图片描述


二叉排序树的查找效率

二叉排序树查找算法的平均查找长度，主要取决于树的高度，即与二叉树的形态有关。

查找成功的平均查找长度为：  Σ(本层高度*本层结点个数) / 结点总数
查找不成功的平均查找长度为：   Σ(本层高度*本层补上的叶子结点个数) / 补上的叶子总数

如图所示的二叉排序树：
在这里插入图片描述

查找成功的平均查找长度为：（1*1 + 2*2 + 3*3 + 4*3）/ 9

在这里插入图片描述

查找不成功的平均查找长度：（2*1 + 3*3 + 4*6）/ 10

薛定谔的猫ovo
关注
  • 124
    点赞
  • 踩
  • 811
    收藏
    觉得还不错? 一键收藏
  • 17
    评论
专栏目录
c++封装的二叉排序树， c++ 封装 二叉排序树 私有成员函数递归 非递归的插入 实现的树的各种操作。
04-23
c++ 封装 二叉排序树 私有成员函数递归 非递归的插入 实现的树的各种操作，并且利用c++的面向对象思想进行封装，内部包含三个文件BinaryTree.cpp， BinaryTree.hpp ， main.cpp
c++封装的二叉排序树
04-24
c++ 封装 二叉排序树 私有成员函数递归 非递归的插入 实现的树的各种操作，并且利用c++的面向对象思想进行封装，内部包含三个文件BinaryTree.cpp， BinaryTree.hpp ， main.cpp 非递归的插入 实现的树的各种操作， 私有成员函数递归。
二叉搜索树（二叉排序树，二叉查找树）（附图详解+代码实现+应用分析）
最新发布
2301_77509762的博客
03-25 1354
二叉搜索树，二叉搜索树的概念，二叉搜索树的操作（含思路分析+代码实现），二叉搜索树的查找（递归实现看最后总代码），二叉搜索树的插入（递归实现看最后总代码），二叉搜索树的删除（递归实现看最后总代码，总代码（含递归实现）：，二叉搜索树的应用，二叉搜索树的性能分析
二叉排序树的相关代码（插入，删除，创建，遍历）
12-18
二叉排序树（Binary Sorting Tree）又称二叉搜索树（Binary Search Tree），是一种特殊结构的二叉数，作为一种排序和查找的手段，对应有序表的对半查找，通常亦被称为数表。其定义也是递归的。 二叉排序树的定义： 每个节点都有一个作为搜索依据的关键码（key），所有节点的关键码互不相同； 二叉排序树或者是空树或者是具有下述性质的二叉数， ①其左子树上所有结点的数据值均小于根结点的数据值； ②右子树上所有结点的数据值均大于根结点的数据值； ③左子树和右子树又各是一棵二叉排序树。 二叉排序树用中序遍历就可以得到由小到大的有序序列
二叉排序树最新版本.pdf
04-21
1.2.1编程实现二叉排序树，包括生成、插入，删除； 1.2.2对二叉排序树进行先根、中根、和后根非递归遍历； 1.2.3每次对树的修改操作和遍历操作的显示结果都需要在屏幕上用树的形状表示出来。 1.2.4分别用二叉排序树和数组去存储一个班(50 人以上)的成员信息(至少包括学号、姓名、成绩 3 项),对比查找效率，并说明在什么情况下二叉排序树效率高,为什么?
二叉排序树构建 （学生）.c
10-24
二叉排序树构建 （学生）.c
数据结构-二叉排序树（图文详细版）
淡沫初夏zz的博客
01-17 5万+
二叉排序树
数据结构-----二叉排序树
m0_73633088的博客
10-01 6980
今天我们继续学习新的知识点----排序二叉树，在此之前我们学习了相关的排序算法，给你一个数组，然后对这个数组进行排序。那么同样的我们也可以去构建一个二叉排序树，在创建树的过程中进行排序，也能实现排序的效果，下面就一起来看看吧！二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。是数据结构中的一类。在一般情况下，查询效率比链表结构要高。给定一个二叉树，如果满足以下条件，那就是二叉排序树。
二叉排序树（二叉查找树、二叉搜索树）（图解+完整代码）
热门推荐
weixin_54186646的博客
04-25 7万+
图解二叉排序树（二叉查找树、二叉搜索树）的插入操作、查找操作、删除操作以及完整的代码实现
数据结构-二叉排序树（BST树）
理科男同学
11-15 8929
1，二叉排序树介绍 二叉排序树（Binary Sort Tree）或者是一颗空树；或者是具有如下性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树又分别为二叉排序树。 显然二叉排序树的定义是一个递归形式的定义，所以后面景禹要讲的插入、查找和删除都是基于递归的形式。特别说明：如果有相同的值，可以将该节点放在左子节点或右子节点 1.1，二叉排序树的构建 假设我们有初始的无序...
二叉排序树详解
云杉木屋
04-01 2万+
摘要：本篇笔记专门介绍二叉排序树，重点讲解了二叉排序树的特性，以及二叉排序树各方面的基本实现。
二叉排序树的建立、插入、查找和删除
08-04
代码里有二叉排序树插入操作递归算法，二叉排序树插入操作非递归算法，二叉排序树删除操作，创建二叉排序树，二叉排序树查找递归算法，二叉排序树查找非递归算法
C++搜索二叉树的查找、插入、删除
MilkLeong的博客
02-15 2243
以一年十二月的英文缩写为键值而产生二叉搜索树，查找其中的Feb值，及输出最小、最大值： 红框以内为输出，红框以外为输入。
C++生成二叉搜索树，以及数据的查找，删除和插入
m0_56350559的博客
06-09 164
C++二叉排序树的实现
二叉搜索树的插入,查找,删除和遍历(c/c++)
weixin_42480264的博客
08-19 2208
二叉搜索树的建立 二叉搜索树的建立即为向二叉树中插入元素.开始插入第一个元素时,二叉搜索树是空树,直接申请一个内存空间将元素放入树中.再插入元素时,从根节点开始比较,若待插入的元素值较大,则树中节点向右走,若较小,则树中节点向左走,直到找到一个空位置,将节点插入. 二叉搜索树中查找元素 在二叉搜索树中查找元素时,先将元素与根节点值比较,若元素的值较小,则根节点向左走(root = root-...
二叉排序树BST的插入、查找实现(递归和非递归)
qq_45512400的博客
09-22 769
#include<stdio.h> #include<stdbool.h> #include<stdlib.h> typedef int ElemType; typedef struct BiTNode{ ElemType data; struct BiTNode *lchild,*rchild; }BiTNode,*BiTree; //递归实现 bool BST_insert(BiTree T,ElemType key){ if(T->data==-1)
二叉树（排序树）的创建、遍历、插入、删除以及查找
weixin_43126491的博客
08-11 3540
二叉树（排序树）的创建、遍历、插入、删除以及查找 原理：二叉树的先序创建（递归）按先序遍历的顺序，依次 输入结点的信息建成立二叉链表的算法。该算法的基本思想是：首先对一般的二叉树添加若干个虚结点，使每一个节点都有左右两个孩子，然后依次输入结点信息。若输入的结不是虚结点，则建立一个新结点；先序创建左子树；先序创建右子树 在这里插入代码片 ...
详解数据结构——二叉排序树
莫浅子的博客
10-29 1万+
二叉排序树，又称二叉查找树（BST，Binary Search Tree)一棵二叉树或者是空二叉树，或者是具有如下性质的二叉树: 左子树上所有结点的关键字均小于根结点的关键字; 右子树上所有结点的关键字均大于根结点的关键字。左子树和右子树又各是一棵二叉排序树 左子树结点值
数据结构（34）二叉排序树
李白
06-20 9717
目录 1、二叉排序树（BST,Binary Sort Tree）定义 2、二叉排序树的查找 3、二叉排序树的插入 4、二叉排序树的构造 6、二叉排序树的查找效率分析 7、二叉排序树与二分排序对比 1、二叉排序树（BST,Binary Sort Tree）定义 二叉排序树（也称为二叉查找树）或者是一棵空树，或者是具有以下特性的二叉树： 1）若左子树非空，则左子树上所有结点的值均小于根节点的值。 2）若右子树非空，则右子树上所有结点的值均大于根节点的值。 3）左、右子树也分别是一棵二叉排序
二叉排序树非递归插入算法
11-06
二叉排序树非递归插入算法是一种在二叉排序树中插入新节点的方法，它不使用递归，而是使用循环来实现。具体实现方法如下： 1. 首先，创建一个新节点，并将要插入的值存储在该节点中。 2. 然后，从根节点开始遍历二叉排序树，直到找到一个空节点为止。 3. 在遍历过程中，如果要插入的值比当前节点的值小，则继续遍历当前节点的左子树；如果要插入的值比当前节点的值大，则继续遍历当前节点的右子树。 4. 当找到一个空节点时，将新节点插入到该位置。 5. 最后，返回根节点。 下面是二叉排序树非递归插入算法的代码实现： ```C++ void insert(T value) { TreeNode<T> *node = new TreeNode<T>(value); if (root == NULL) { root = node; return; } TreeNode<T> *current = root; while (true) { if (value < current->val) { if (current->left == NULL) { current->left = node; break; } current = current->left; } else { if (current->right == NULL) { current->right = node; break; } current = current->right; } } } ```

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 17
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值