光线追踪渲染实战：蒙特卡洛路径追踪及其c++实现

项目代码仓库：
GitHub：https://github.com/AKGWSB/EzRT
gitee：https://gitee.com/AKGWSB/EzRT

写在前面

这两天微信打算换个头像，于是打算弄个光追的小渲染器来渲染新头像。。。下面是结果：

多贴几张不同渲染滴图片：

---

要实现光线追踪可不容易，最近我也在网上看了一些他人的博客和资料，基本上要么是笼统的理论介绍，贴几个高大上的数学公式，或者是 ppt 的截图，然后就是你复制我我复制你的内容，最后贴几张渲染的结果。我看完他们写的之后基本都是一脸懵 β 不知所措，我太菜了

…

于是我打算自己写一篇博客。以【把大象装进冰箱】进行比喻：如果说网络上的资料是【打开门，送大象进去，关门】的话，那本篇博客就是讨论【怎么装】的。比如冰箱门把手在哪里，朝哪个方向拉才能打开冰箱，要用香蕉还是鞭子把大象赶进去，怎么关上冰箱的门…

批话不多说，直接开始正文的内容!

光线追踪简介

在传统的计算机图形学中，通常使用光栅化的方法来生成像素。因为光栅化之后我们只选取我们看到的图形，视野之外的几何信息被裁剪，导致场景的全局信息丢失。那么就会造成一些渲染上的 “不正确”，比如水面只能反射我们屏幕看到的像素：

此外，一些基于全局信息的渲染效果不能很好的运行，比如全局光照。在光栅管线下我们往往需要通过各种近似算法去模拟真实世界的光影现象，非常麻烦并且效果 “还凑合”

---

光线追踪超越了传统的图形流水线，是一种 现代 的渲染。光线追踪是一种基于物理的渲染方法，通过模拟光在介质中的真实表现来输出足以逼近现实的图像。光线从光源出发，经过各种反射折射，进入摄像机：

因为从光源出发有 无数条 到达相机的路线，正向地从灯泡开始模拟光的传播变得不是很现实，于是曲线救国，转而从相机方向开始向场景投射射线，试图找出到达光源的可能路径：

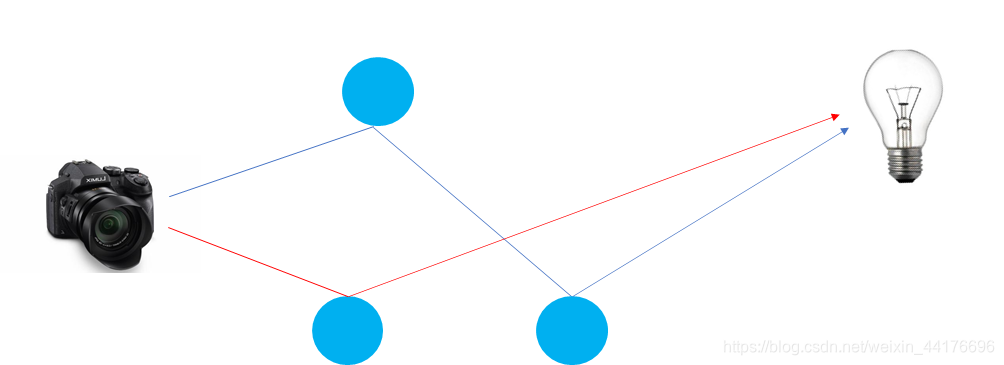
本篇博客代码主要实现的是路径追踪技术。路径追踪技术是光线追踪的一个分支，通过向场景中投射光线，并且模拟光线的行径，在物体和光源之间找出一条条可行的路径，最后返回积累的颜色。

---

和光栅化不同，光线追踪的第一步是向世界空间中投射光线，这一步叫做 RayCasting，投射的光线碰到哪个实体，我们对应位置的像素就代表该实体，同时要给对应位置的像素赋以一定的颜色：

假设我们发射的光线命中了一个点，我们就返回这个点的颜色作为最终像素的颜色。

那么怎样描述一点的颜色呢？我们引入渲染方程 ↓

渲染方程

故事要从 元和二年 1986 年开始说起，科学家首次提出渲染方程，以描述一个点受到的光照的影响。渲染一个像素的颜色就是求解渲染方程的过程。大致意思是这样的：一个点的光照由 2 部分组成，分别是：

1. 该点自己发出的光
2. 来自任意方向上的光打到该点积累形成的光

注意这个任意方向，允许该点接收来自其 法向半球 范围内方向的入射光：

那么想要计算来自法向半球内任意方向的入射光的积累，我们必须计算一个 半球积分！ 这里给出渲染方程的简化形式：

$$L\left(p\right)=E\left(p\right)+{\int }_{}L\left(q\right)\ast cos(\theta )\mathrm{d}{\omega }_i$$

其中符号的解释如下：

$$\begin{array}{l}L(x)\to x点的光强度\\ E(x)\to x点发出的光\\ q\to 从p点出发,方向为{\omega }_i的光命中了q点的物体\\ \theta \to {\omega }_i与q点法向量的夹角\end{array}$$

此外，${\int }_{}$ 就是对法向半球入（出）射光线方向的积分。注意到渲染方程的 递归 形式，要想求解 p 点的光照我们必须先递归计算 q 点的光照值，如图：

递归式告诉我们：q 点也反射了光到 p 点，反射光的强度等于 q 点的光强度乘以反射到 p 点的百分比 cos(θ）

注：


这里有个错误，我写的是 θ 是出射光 wi 和命中点 q 的法线的夹角，实际上渲染方程中，θ 是出射光 wi 和出发点 p 点的法线的夹角，也就是 Lambert’s cosine law ，或者说 phong 光照模型中的 N dot L


这个错误我在写完博客的半年之后才发现。。。不过因为我们用的是简化版的渲染方程，并非基于物理，即使你去掉这个 cosine，也能够得到相对不错的结果，真正正确的伪代码应该是：

至于这里为啥使用错误的图，得到的图片仍然在一定程度上符合物理定律呢？我猜测是这样的：

民科警告⚠

对于 p 点的单位面积 dp，光能够发射到 q 点的比率，取决于 dp 在入射光方向上面的投影面积：

---

了解了渲染方程的成分，就可以进行渲染方程的求解了。在高等数学中，积分的计算需要找到被积函数的原函数，和积分变量。可是渲染方程是一个困难积分，无法精确地计算其原函数，于是需要找寻其他方法对困难积分进行计算。

那么怎样计算一个困难积分的？我们引入蒙特卡洛方法 ↓

蒙特卡洛方法

我更愿意称之为丢豆子。考虑最直观的情况，欲求区间上一函数的积分，我们往 x 区间上面丢豆子，并且计算豆子命中的位置的 y 的值，最后把他们加起来作为积分的估计：

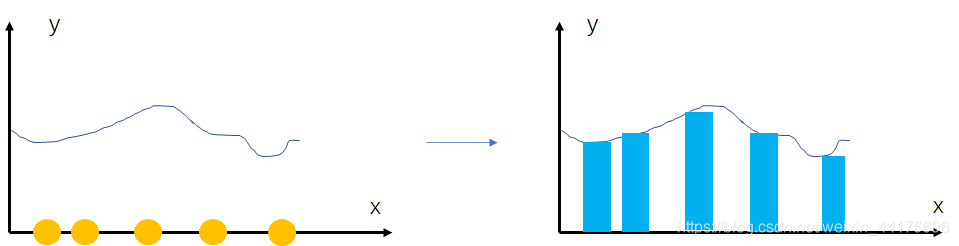
丢豆子的过程称之为【采样】，如果我们使用 均匀分布 的 x 进行丢豆子，就能得到上图等宽度的柱状图近似。

事实上在实际问题中，豆子的位置不会总是服从均匀分布。那么每一个豆子的贡献，除了豆子命中位置的 y 值，还取决于豆子 命中该位置的概率。蒙特卡洛方法允许我们使用 x 的任意的概率密度函数，来对积分进行估计。

假设采样 x 的概率密度函数为 $PDF(x)$，被积函数为 $f(x)$，那么 x 点采样的贡献就是：

$$\frac{f(x)}{PDF(x)}$$

所以积分计算就很简单了。首先按照产生一堆符合概率密度函数 PDF 分布的随机变量 x，然后对每一个 x 都计算 $\frac{f(x)}{PDF(x)}$ 最后求他们的 均值 即可。现在回过头来看刚刚的均匀分布的丢豆子，其中 $PDF(x)=\frac{1}{b-a}$，那么我们估计 $x^2$ 的积分就可以这么计算：

可以看到仅 5 次采样就可以获得还不错的结果。我们和真实的积分值十分逼近了！采样的次数越多，差异就越少，所以蒙特卡洛方法可以做到对积分结果的 无偏 估计，这是好特性。

知晓了困难积分的近似求解方式，我们开始正式求解渲染方程 ↓

渲染方程求解伪代码

渲染方程是对于被求解点 p 的法向半球的积分，那么我们的随机变量就是在法向半球内的射线的方向，假设我们取法向半球内 均匀分布的射线 方向，那么就有 $PDF(x)=\frac{1}{2\pi }$，因为半球面积就是 $2\pi$，如图：

于是有如下的伪代码：

pathTracing(p)
{
   
	L = 0.0
	for(i in SAMPLE)
	{
   
		wi = random()	// 随机选择一个方向
		if(wi hit q)	// 射线 wi 击中 q 点
		{
   
			cosine = dot(nq, wi)	// q 点法向量 nq 和 wi 的夹角余弦值
			L += cosine * pathTracing(q) / PDF(wi)
		}
	}
	return L / SAMPLE	// 返回均值
}

其中 SAMPLE 就是我们的采样次数。那么问题就来了，这个递归的复杂度是指数，复杂度非常高带来的就是极大的计算资源的消耗，因为光线会有爆炸般的增长，以 SAMPLE=100 为例：

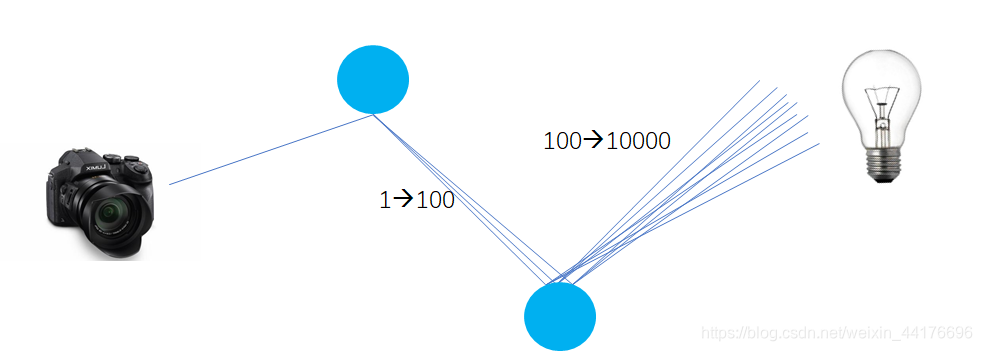
那么我们只有限制 SAMPLE=1 才能防止指数增长。而一次采样的估计肯定是不准确的，于是我们对每个像素，发射多条光线，然后平均他们的结果。每个像素的光线数目叫做 SPP，即（Sample Pre Pixel），下图演示了 SPP=3 的情况，我们找寻了 3 条到光源的路径，并且平均他们的贡献：

注意只有在第一次采样时发射若干条光线，其余的时候我们只随机选取一个方向发射光线并且递归计算。那么伪代码就改成：

// 追踪一条光线
pathTracing(p)
{
   
	L = 0.0
	wi = random()	// 随机选择一个方向
	if(wi hit q)	// 射线 wi 击中 q 点
	{
   
		cosine = dot(nq, wi)	// q 点法向量 nq 和 wi 的夹角余弦值
		L += cosine * pathTracing(q) / PDF(wi)
	}

	return L
}

// 对一个像素投射 SPP 条光线
L = 0.0
for(i in SPP)
{
   
	wi = random()	// 随机选择一个方向
	if(wi hit q)	// 射线 wi 击中 q 点
	{
   
		L += pathTracing(q) / PDF(wi)
	}
}
L /= SPP

这一步也没啥特别的，就是向每一个像素投射光线，然后求解渲染方程，没了。。。

渲染方程的伪代码有了，我们通过 c++ 实现它 ↓

编程前的准备

着手编写一个在 Windows 10 下运行的 x64 程序，程序以图片的形式输出场景的渲染结果。我们以 Vusial Studio 2019 作为 IDE，此外我们还需要额外的帮助库。

数学运算库

首先是数学运算库，我们需要一个能够表示 三维向量，并且对向量进行加减乘除点积叉乘等操作的帮助库。你可以自己写一个简易的 class，也可以使用现成的第三方库，这里我使用的是 glm，它的网站在 这里，你也可以从它的 GitHub 上面获取。此外，也可以通过 vcpkg 包管理工具来下载，只需要运行命令：

vcpkg install glm

如果在安装时遇到任何困难，可以参考我以前的博客：传送门①，传送门②

图像输出

你可以使用任何流行的图像处理的库来进行图像输出，他们可以是 Opencv，Qt，甚至是 OpenGL，但是这里我使用非常轻量级的 svpng。svpng 不是一个 c++ 的第三方库，它仅是一个 inc文件：

你只需要把它放在你的工程目录下，然后再 #include "svpng.inc" 即可调用它。svpng 就一个非常简单的功能，就可以帮我们保存 png 图像，调用 svpng 函数即可。函数的原型长这样：

void svpng(FILE* fp, unsigned w, unsigned h, const unsigned char* img, int alpha)

其中 FILE 是文件指针，w 和 h 是图片的宽度和高度，img 是图像的像素值数组，alpha 是透明度，我们填 0 即可。通过如下的代码就可以将一个范围在 [0, 1] 之间的 double 浮点数 buffer 输出到图片上：

// 输出 SRC 数组中的数据到图像
void imshow(double* SRC)
{
   
    
    unsigned char* image = new unsigned char[WIDTH * HEIGHT * 3];// 图像buffer
    unsigned char* p = image;
    double* S = SRC;    // 源数据

    FILE* fp;
    fopen_s(&fp, "image.png", "wb");

    for (int i = 0; i < HEIGHT; i++)
    {
   
        for (int j = 0; j < WIDTH; j++)
        {
   
            *p++ = (unsigned char)clamp((*S++) * 255, 0.0, 255.0);  // R 通道
            *p++ = (unsigned char)clamp((*S++) * 255, 0.0, 255.0);  // G 通道
            *p++ = (unsigned char)clamp((*S++) * 255, 0.0, 255.0);  // B 通道
        }
    }

    svpng(fp, WIDTH, HEIGHT, image, 0);
}

clamp 是截断函数，glm 库带的，如果报错那么您可以删掉它并且换成您自己的 clamp，只是时刻注意 SRC 是 [0, 1] 范围的 double，我们习惯这么表示颜色，同时方便计算，不容易被截断。此外，svpng 默认图像的 RGB 通道是相邻的，我们直接利用指针进行遍历即可。

随便在 SRC 中写点什么，比如输出 xy 的值作为 rg 通道。如果你看到如下的图片被生成，那么很成功！

如果找不到 svpng.inc 那么检查你的 vs 工程是否配置正确，将包含 svpng 的目录添加到 vs 的 include 目录：

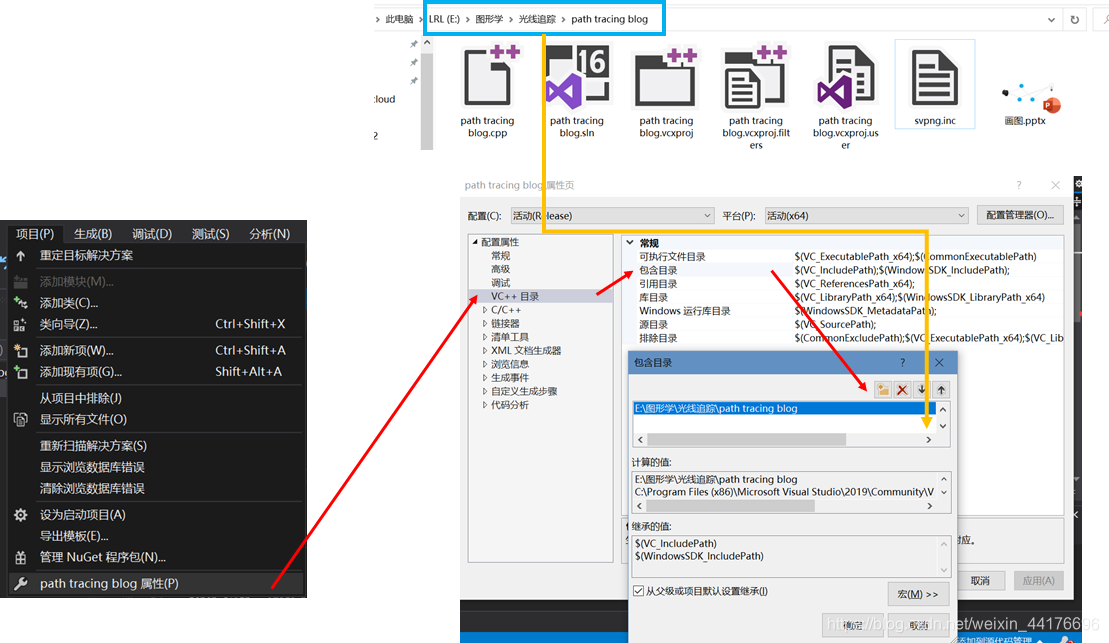
多线程加速

光线追踪运算量巨大，单靠简单的单线程程序无法高效执行，但是因为 每个光线的采样是相互独立的，于是我们可以利用多线程加速。Visual Studio 有自带多线程加速的 openmp 库，无需 自己手动下载，只需要引入：

#include <omp.h>    // openmp多线程加速

同时在项目设置中，允许 vs 使用多线程：

然后在需要并行执行的 for 循环之前加上：

omp_set_num_threads(50); // 线程个数
#pragma omp parallel for

for()
{
   
	...
}

就可以享受多线程加速的福利了。此外，我墙裂建议你打开 O2 优化同时将运行模式调整到 Release，以获取最大运行速度：

一切就绪？我们准备进入光与粒的世界 ↓

相机配置与光线生成

光线追踪的第一步是投射光线，我们模拟相机投影与成像的规则，指定一个 [-1, 1] 范围内的投影平面和一个视点，然后根据输出图片的像素位置，计算其对应投影平面上的坐标，最后用坐标减去视点坐标，得到 视线的方向向量，如图：

值得注意的是，图片的 xy 轴原点是在图片左上方，而实际投影我们需要一个在左下方的原点（即平面几何坐标系），所以 y 要做一次 flip。此外，在世界坐标系下，我们确定相机的位置和投影平面的位置，让相机看向 z 轴负方向：

相机配置就绪，我们尝试 输出相机的射线投射方向，其中 imshow 是上面编写的显示图片的函数：

double* image = new double[WIDTH * HEIGHT * 3];
memset(image, 0.0, sizeof(double) * WIDTH * HEIGHT * 3);
double* p = image;
for (int i = 0; i < HEIGHT; i++)
{
   
    for (int j = 0; j < WIDTH; j++)
    {
   
        // 像素坐标转投影平面坐标
        double x = 2.0