项目代码仓库:
GitHub:https://github.com/AKGWSB/EzRT
gitee:https://gitee.com/AKGWSB/EzRT
前言
利用 BVH 数据结构加速光线追踪遍历!

在上次的博客:光线追踪渲染实战:蒙特卡洛路径追踪及其c++实现 里面,我们实现了最简单的光线追踪渲染 demo
但是注意到这个程序的效率并不高,因为我们大量的时间都用在了【光线和三角形求交】这个部分,事实上求交操作也是光线追踪技术性能的瓶颈。注意到下面的简单场景仅仅包含十几个图元(三角形和球体),但是渲染一张 256 x 256 的图片,采样 4096 spp,就消耗了数十分钟:

效率的低下是因为每次求交我们都枚举了场景中的所有图元,即:
// 遍历所有图形,求最近交点
for (auto& shape : shapes)
{
r = shape->intersect(ray);
...
}
如果说渲染一个小的场景,直接枚举就足够了。但是在现代计算机图形学中,场景的三角形数目一般都是按 K 或 M,即 1 0 3 10^3 103 和 1 0 6 10^6 106 来计算的。比如经典的 Sponza Atrium 就拥有 29 K 个多边形:

如果暴力遍历所有三角形,那么时间开销之大,以至于我们的程序慢到可以和银河系中间的大黑洞比一比谁先结束
于是 BVH 树的出现了,为了解决冗长的求交问题。事实上光线和大多数三角形都是不相交的,所以 BVH 树能够根据光线和场景的三维空间关系,每次剔除半数的三角形,减少冗余的求交,达到加速效果
BVH 简介
BVH 全称 Bounding Volume Hierarchy,即层次包围盒。BVH 用 AABB 的盒子(碰撞箱)包围一组三角面片:

注:
AABB 包围盒就是轴对称包围盒
即盒子的 6 个面平行于 xy, xz, yz 平面
光线要击中盒子中的三角形的 必要条件 是光线击中盒子,如果光线没有击中盒子,那么必定不会击中盒子里面的所有三角形。
基于这个规律,如果我们将三角形对半分,用两个盒子来分别容纳,就可以简单的用光线和盒子的求交,剔除半数的三角形,从而达到减少求交次数的目的:

对于左边和右边的盒子,可以递归地再次进行划分,形成树形结构:

光线与左边的盒子不相交,那么左半边的所有三角形,都不不用考虑了。这与平衡二叉树的搜索类似,一次排除半数元素,将查找的复杂度从 O(n) 变为 O(log(n))
所有的三角形都存储在叶子节点中,而中间节点仅存储 AABB 包围盒。在光线和 BVH 树的根节点求交的时候,有如下的步骤:
- 光线和左盒子求交
- 光线和右盒子求交
- 如果光线命中左盒子,递归对左子树求交
- 如果光线命中右盒子,递归对右子树求交
因为是以三角形为单位进行划分,每个三角形都属于一个盒子,那么盒子之间有可能交错。光线同时命中了左右盒子,就要对两个盒子都递归求交:
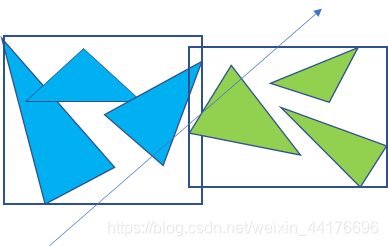
此外,这里左右盒子只是逻辑上的划分,不代表三维空间里的三角形位置。因为每次是将三角形(数组)对半分
构建 BVH 树
以经典的 Stanford Bunny 为例,它包含 4968 个三角形:

你可以在 这里 找到这只兔子的 obj 格式的模型
假设我们已经成功读取了 obj 模型的所有顶点和面片索引。如果读取 obj 遇到困难,可以参考我之前的博客:OpenGL学习(六)纹理与obj格式模型的读取
我们根据这些信息创建所有的三角形。首先是三角形的结构体定义:
typedef struct Triangle {
vec3 p1, p2, p3; // 三点
vec3 center; // 中心
Triangle(vec3 a, vec3 b, vec3 c) {
p1 = a, p2 = b, p3 = c;
center = (p1 + p2 + p3) / vec3(3, 3, 3);
}
} Triangle;
这里除了三个点以外还定义了中心,因为待会我们对三角形进行对半分,要根据其中心位置进行划分
划分的方式也很简单。按照某个轴进行排序,然后将数组对半分。排序的比较函数如下:
// 按照三角形中心排序 -- 比较函数
bool cmpx(const Triangle& t1, const Triangle& t2) {
return t1.center.x < t2.center.x;
}
bool cmpy(const Triangle& t1, const Triangle& t2) {
return t1.center.y < t2.center.y;
}
bool cmpz(const Triangle& t1, const Triangle& t2) {
return t1.center.z < t2.center.z;
}
紧接着需要根据 obj 文件的信息,创建三角形的数组:
std::vector<Triangle> triangles;
最后我们需要一个 BVH 树的节点。它需要包含一些信息,比如包围盒 AABB,还有叶子节点信息:
这里保存一个 n 和 一个 index,其中 n 不为 0 时表示是叶子节点,n 是存储的三角形的个数,而 triangles 数组中 [index, index + n -1] 范围的三角形都属于该节点
最后是指向两个子树的指针,于是 BVHNode 结构体的定义如下:
// BVH 树节点
struct BVHNode {
BVHNode* left = NULL; // 左右子树索引
BVHNode* right = NULL;
int n, index; // 叶子节点信息
vec3 AA, BB; // 碰撞盒
};
注:
这里规定 AA 是包围盒的数值小的坐标,BB 是数值大的坐标,比如:此外,在代码中 AABB 都是三维的坐标
然后可以开始建树:
- 首先拿到一个三角形数组和左右下标
l, r - 然后遍历
[l, r]中所有三角形,计算 x,y,z 轴的最小最大值,从而获得本节点的 AABB 碰撞箱 - 如果仅剩节点数目小于阈值 n,直接构建并且返回叶子节点,否则递归建树
- 选取 AABB 碰撞箱 最长 的一个轴,对三角形按照对应轴的中心坐标进行 排序
- 根据数组中点
mid将三角形序列分为左半边[l, mid]和右半边[mid+1, r],递归进行建树
代码如下:
// 构建 BVH
BVHNode* buildBVH(std::vector<Triangle>& triangles, int l, int r, int n) {
if (l > r) return 0;
BVHNode* node = new BVHNode();
node->AA = vec3(1145141919, 1145141919, 1145141919);
node->BB = vec3(-1145141919, -1145141919, -1145141919);
// 计算 AABB
for (int i = l; i <= r; i++) {
// 最小点 AA
float minx = min(triangles[i].p1.x, min(triangles[i].p2.x, triangles[i].p3.x));
float miny = min(triangles[i].p1.y, min(triangles[i].p2.y, triangles[i].p3.y));
float minz = min(triangles[i].p1.z, min(triangles[i].p2.z, triangles[i].p3.z));
node->AA.x = min(node->AA.x, minx);
node->AA.y = min(node->AA.y, miny);
node->AA.z = min(node->AA.z, minz);
// 最大点 BB
float maxx = max(triangles[i].p1.x, max(triangles[i].p2.x, triangles[i].p3.x));
float maxy = max(triangles[i].p1.y, max(triangles[i].p2.y, triangles[i].p3.y));
float maxz = max(triangles[i].p1.z, max(triangles[i].p2.z, triangles[i].p3.z));
node->BB.x = max(node->BB.x, maxx);
node->BB.y = max(node->BB.y, maxy);
node->BB.z = max(node->BB.z, maxz);
}
// 不多于 n 个三角形 返回叶子节点
if ((r - l + 1) <= n) {
node->n = r - l + 1;
node->index = l;
return node;
}
// 否则递归建树
float lenx = node->BB.x - node->AA.x;
float leny = node->BB.y - node->AA.y;
float lenz = node->BB.z - node->AA.z;
// 按 x 划分
if (lenx >= leny && lenx >= lenz)
std::sort(triangles.begin() + l, triangles.begin() + r + 1, cmpx);
// 按 y 划分
if (leny >= lenx && leny >= lenz)
std::sort(triangles.begin() + l, triangles.begin() + r + 1, cmpy);
// 按 z 划分
if (lenz >= lenx && lenz >= leny)
std::sort(triangles.begin() + l, triangles.begin() + r + 1, cmpz);
// 递归
int mid = (l + r) / 2;
node->left = buildBVH(triangles, l, mid, n);
node->right = buildBVH(triangles, mid + 1, r, n);
return node;
}
可视化的建树结果,首先是整个模型碰撞箱,然后进行二分,再二分,以此类推。下图以从上到下从左到右的顺序展示了二分建树的过程:

可以看到,层次越深,包围盒就越小,越多,越精确
光线和 AABB 盒子求交
要在 BVH 上求交,首先要解决的是光线和 BVH 盒子求交的问题。首先定义光线:
// 光线
typedef struct Ray {
vec3 startPoint = vec3(0, 0, 0); // 起点
vec3 direction = vec3(0, 0, 0); // 方向
} Ray;
然后对于 AABB 盒子,因为是轴对齐的包围盒,只需要找出一组【穿入,穿出】点,即能说明光线击中盒子:

对于轴对齐包围盒,拥有三对平行的面,分别是 x,y,z 面,对于每一组面,都要计算【穿入,穿出】点:

如果光线起点距离穿入点的距离 小于 光线起点距离穿出点的距离,即 t0 < t1 则说明命中:

首先计算起点到各个面的距离,以二维为例,用 AA 的坐标除以光线方向 direction 可以得到二维向量 in,其中 in.x 是 x 面的穿入点,in.y 是 y 面的穿入点。同理 BB 的坐标除以 direction 得到 out 也是一样:
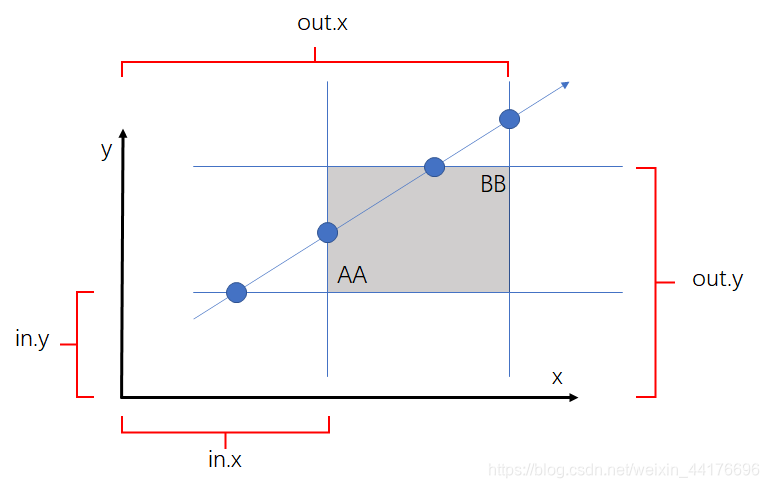
然后我们取 out 中最小的距离记作 t1,和 in 中最大的距离记作 t0,然后看是否 t1 > t0 如果满足等式,则说明命中:

这个结论推广到三维也是成立的,于是可以很快得出和 AABB 盒子求交的代码:
// 和 aabb 盒子求交,没有交点则返回 -1
float hitAABB(Ray r, vec3 AA, vec3 BB) {
// 1.0 / direction
vec3 invdir = vec3(1.0 / r.direction.x, 1.0 / r.direction.y, 1.0 / r.direction.z);
vec3 in = (BB - r.startPoint) * invdir;
vec3 out = (AA - r.startPoint) * invdir;
vec3 tmax = max(in, out);
vec3 tmin = min(in, out);
float t1 = min(tmax.x, min(tmax.y, tmax.z));
float t0 = max(tmin.x, max(tmin.y, tmin.z));
return (t1 >= t0) ? ((t0 > 0.0) ? (t0) : (t1)) : (-1);
}
注:
这里计算 invdir 是因为 glm 这个库不支持向量直接除运算符
而且预计算除法可以减小计算开销
光线在 BVH 上求交
首先定义一个求交的结果,因为我们不仅需要返回命中的三角形,还要返回起点到它的 距离 ,这是因为遍历 BVH 时可能会产生两个交点:

但是最终我们需要选取最近的交点,可以通过距离来判断。于是有求交结果的定义:
// 求交结果
struct HitResult {
Triangle* triangle = NULL;
float distance = INF;
};
紧接着是和三角形求交。首先判断光线和三角形所在平面是否相交,然后判断交点是否在平面内,原理如下:

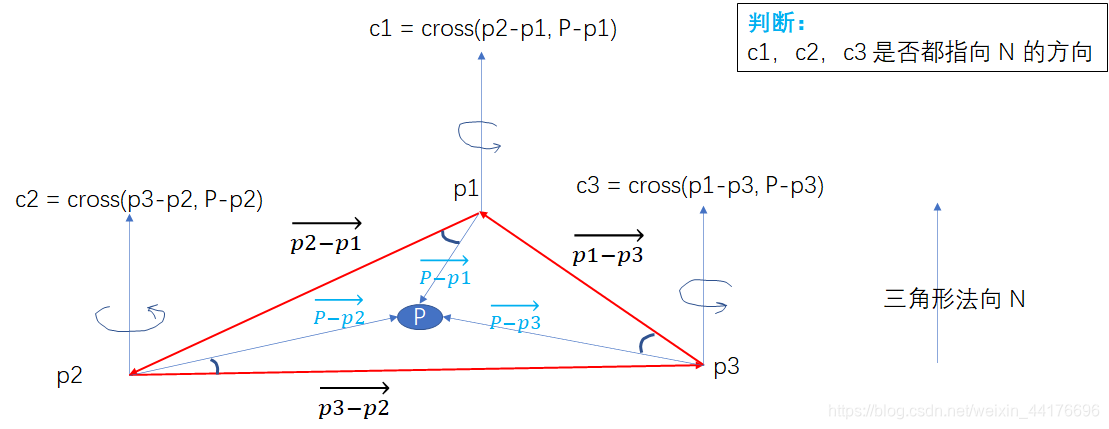
于是和三角形求交的代码如下,如果没有交点,我们返回 INF 即一个大数:
// 光线和三角形求交
float hitTriangle(Triangle* triangle, Ray ray) {
vec3 p1 = triangle->p1, p2 = triangle->p2, p3 = triangle->p3;
vec3 S = ray.startPoint; // 射线起点
vec3 d = ray.direction; // 射线方向
vec3 N = normalize(cross(p2 - p1, p3 - p1)); // 法向量
if (dot(N, d) > 0.0f) N = -N; // 获取正确的法向量
// 如果视线和三角形平行
if (fabs(dot(N, d)) < 0.00001f) return INF;
// 距离
float t = (dot(N, p1) - dot(S, N)) / dot(d, N);
if (t < 0.0005f) return INF; // 如果三角形在光线背面
// 交点计算
vec3 P = S + d * t;
// 判断交点是否在三角形中
vec3 c1 = cross(p2 - p1, P - p1);
vec3 c2 = cross(p3 - p2, P - p2);
vec3 c3 = cross(p1 - p3, P - p3);
if (dot(c1, N) > 0 && dot(c2, N) > 0 && dot(c3, N) > 0) return t;
if (dot(c1, N) < 0 && dot(c2, N) < 0 && dot(c3, N) < 0) return t;
return INF;
}
于是我们可以在 triangle 数组的某个下标范围 [l, r] 里面,暴力查找最近的三角形:
// 暴力查数组
HitResult hitTriangleArray(Ray ray, std::vector<Triangle>& triangles, int l, int r) {
HitResult res;
for (int i = l; i <= r; i++) {
float d = hitTriangle(&triangles[i], ray);
if (d < INF && d < res.distance) {
res.distance = d;
res.triangle = &triangles[i];
}
}
return res;
}
然后编写和 BVH 求交的代码。它返回击中的三角形的指针,如果未命中则返回空指针。光线求交操作也是递归操作,首先和左右子树的 AABB 盒子求交,如果击中盒子,就递归左右子树,否则停止。此外如果遇到叶子节点,应该和叶子节点包围的 所有 三角形求交:
// 在 BVH 上遍历求交
HitResult hitBVH(Ray ray, std::vector<Triangle>& triangles, BVHNode* root) {
if (root == NULL) return HitResult();
// 是叶子 暴力查
if (root->n > 0) {
return hitTriangleArray(ray, triangles, root->n, root->n + root->index - 1);
}
// 和左右子树 AABB 求交
float d1 = INF, d2 = INF;
if (root->left) d1 = hitAABB(ray, root->left->AA, root->left->BB);
if (root->right) d2 = hitAABB(ray, root->right->AA, root->right->BB);
// 递归结果
HitResult r1, r2;
if (d1>0) r1 = hitBVH(ray, triangles, root->left);
if (d2>0) r2 = hitBVH(ray, triangles, root->right);
return r1.distance < r2.distance ? r1 : r2;
}
可以看到光线和三角形求交的结果,白色的三角形是击中的三角形:
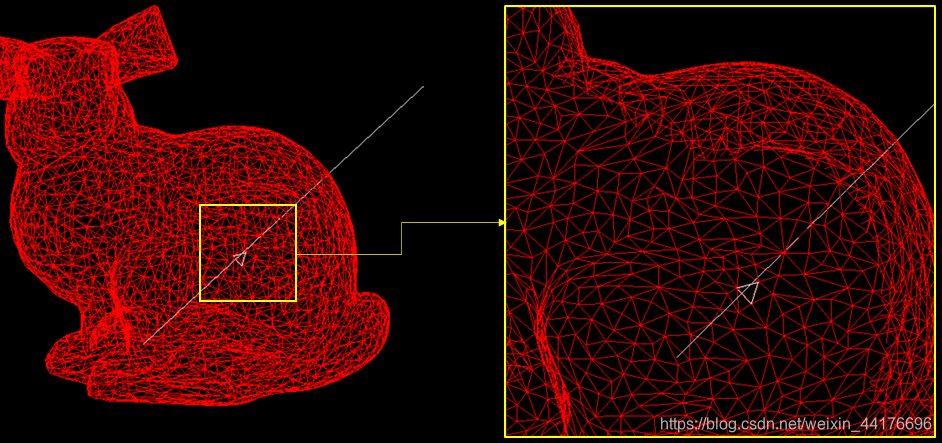
下图以从上到下从左到右的顺序展示了递归遍历 BVH 树的过程,逐层缩小 AABB 碰撞盒,最后精确地定位到极小的区域:

这里只给出了 8 层递归,事实上树不止 8 层,继续遍历以获得更小的 AABB 盒子,以精确定位三角形
SAH 优化(重要)
对于单个的,比较紧凑的网格,使用均分策略进行分割就能够得到不错的效果。但是并非所有场景都能得到好的效果,比如我们多加一个底面:

仅增加两个三角形会对效率带来很大的影响吗?答案是会的。观察增加底面后的新 BVH,这里仅展示第一层的 AABB 盒子:

第一层的两个碰撞盒几乎完全重叠了!这意味着大部分的光线会同时 hit 两个盒子,我们不得不对 两个盒子都进行递归<








 本文介绍了如何使用BVH(Bounding Volume Hierarchy)数据结构来加速光线追踪的遍历过程,通过构建和优化BVH树,减少了光线与场景中图元的求交时间,提高了渲染效率。文章详细阐述了BVH的构建方法,包括AABB盒子求交、SAH优化,并提供了C++代码实现。
本文介绍了如何使用BVH(Bounding Volume Hierarchy)数据结构来加速光线追踪的遍历过程,通过构建和优化BVH树,减少了光线与场景中图元的求交时间,提高了渲染效率。文章详细阐述了BVH的构建方法,包括AABB盒子求交、SAH优化,并提供了C++代码实现。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 271
271

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








