欧拉函数

欧拉函数

1-n中与n互质的数的个数

//单个数的欧拉函数值
int phi(int n){
    int ans=n;
    for(int i=2;i<=sqrt(n);i++){
        if(n%i==0){
            ans=ans/i*(i-1);
            while(n%i==0)n/=i;
        }
    }
    if(n>1)ans=ans/n*(n-1);
    return ans;
}

//欧拉函数打表
//非线性打表
const int maxm=1e6+5;
int phi[maxm];
void init(){
    for(int i=1;i<maxm;i++){
        phi[i]=i;
    }
    for(int i=2;i<maxm;i++){
        if(phi[i]==i){//数值等于本身的是素数
            for(int j=i;j<maxm;j+=i){
                phi[j]=phi[j]/i*(i-1);
            }
        }
    }
}

//欧拉函数线性筛
const int maxm=1e6+5;
int notprime[maxm];
int prime[maxm],cnt;
int phi[maxm];
void Pinit(){
    phi[1]=1;
    for(int i=2;i<maxm;i++){
        if(!notprime[i]){//如果是素数
            prime[cnt++]=i;
            phi[i]=i-1;
        }
        for(int j=0;j<cnt;j++){
            if(prime[j]*i>=maxm)break;
            notprime[prime[j]*i]=1;
            phi[prime[j]*i]=phi[i]*(i%prime[j]?prime[j]-1:prime[j]);
            if(i%prime[j]==0)break;
        }
    }
}

性质:

1.如果p是素数，则φ(p )=p-1，反之，若φ(p )=p-1，则p一定是质数

2.如果p是素数，a是一个正整数，那么φ(p^a)=p^a-p^a-1
证明：φ(p^a)=p^a-(前p^a个数中中和p^a不互质的数)，因为p^a只有一个质因子p，所以前p^a个数中和p^a不互质的数为p的倍数，这样的数为kp(1<=k<=p^a-1)，共有p^a/p个，也就是p^a-1个，所以φ(p^a)=p^a-p^a-1

3.n=p1^a1p2^a2…pk^ak，那么φ(n)=n(1-1/p1)(1-1/p2)…(1-1/pk)

4.n= ∑d|n φ(d) (d包括1和n)

5.若m,n互质，则φ(mn) = φ(m) φ(n) (积性函数)

6.若n为奇数，φ(2n) = φ(n)，因为2和奇数互质，结合欧拉函数是积性函数的性质即可得出这一结论

7.给定整数n，所有小于n且与n互质的数的和是 n∗φ(n)/2

8.若 gcd(n,i)=1 则 gcd(n,n-i)=1

待补充

---

hdu1286 找新朋友

题意：

给n，求1-n中与n互质的数的个数

思路：

模板题，求出n的欧拉函数值即可

---

bzoj2705 Longge的问题

题意:

求∑gcd(i,N) (1<=i<=N)。

思路:

设f(k)为满足gcd(m,n)=k,(1<=m<=n)的个数，则ans=∑(k*f(k)) (k为n的约数)
因为gcd(m,n)=k,所以gcd(m/k,n/k)=1,则f(k)=phi(n/k)，phi为欧拉函数值
O(√n)枚举约数k按上式计算即可

code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
int phi(int n){
    int ans=n;
    for(int i=2;i*i<=n;i++){
        if(n%i==0){
            ans=ans/i*(i-1);
            while(n%i==0)n/=i;
        }
    }
    if(n>1)ans=ans/n*(n-1);
    return ans;
}
signed main(){
    int n;
    while(cin>>n){
        int ans=0;
        for(int i=1;i*i<=n;i++){
            if(n%i==0){
                ans+=i*phi(n/i);
                if(i*i!=n)ans+=(n/i)*phi(i);
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

---

hdu2588 GCD

题意：

给n,m，求有多少个x，满足1<=x<=n且gcd(x,n)>=m

思路：

和bzoj2705原理差不多，
设gcd(x,n)=k，
则gcd(x/k,n/k)=1，x的数量就是欧拉函数值phi(n/k)
注意这题只有满足k>=m的时候才累加进答案
O(√n)枚举因子k即可

code：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int phi(int n){
    int ans=n;
    for(int i=2;i*i<=n;i++){
        if(n%i==0){
            ans=ans/i*(i-1);
            while(n%i==0)n/=i;
        }
    }
    if(n>1)ans=ans/n*(n-1);
    return ans;
}
signed main(){
    int T;
    cin>>T;
    while(T--){
        int n,m;
        cin>>n>>m;
        int ans=0;
        for(int i=1;i*i<=n;i++){
            if(n%i==0){
                if(i>=m){
                    ans+=phi(n/i);
                    if(i*i!=n){
                        if(n/i>=m){
                            ans+=phi(i);
                        }
                    }
                }else{
                    if(n/i>=m){
                        ans+=phi(i);
                    }
                }
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

---

hdu2824 The Euler function

题意：

给l,r求phi[l]+phi[l+1]…+phi[r]

思路:

考察欧拉函数打表，区间和用前缀和来计算
但是这题内存限制很严格，数据范围在3e6，给的内存只能开一个一维数组
所以只能非线性打表(线性需要多数组)，前缀和也要在phi数组上做，即phi[i]+=phi[i-1]

---

hdu4983 Goffi and GCD

题意：

给n,k，求有多少组a,b满足gcd(n-a,n)*gcd(n-b,n)=n^k，答案对1e9+7取模

思路:

当a等于0的时候gcd(n-a,n)为最大值n
当b等于0的时候gcd(n-b,n)为最大值n
所以当a,b都为0的时候gcd(n-a,n)*gcd(n-b,n)等于最大值n²
所以：
1.当k大于2时，无解的，方案数为0
2.当k等于2时，只有a=0,b=0一组解，方案数为1
3.当k等于1时，设gcd(n-a,n)=x，则gcd(n-b,n)=n/x
gcd((n-a)/x,n/x)=1,gcd((n-b)/(n/x),n/(n/x))=1
a有phi(n/x)种，b有phi(x)种
相互匹配，则方案数为phi(n/x)*phi(x)种
又因为ab可以互换，所以还要再乘上2，即phi(n/x)*phi(x)*2
但是当n/x==x的时候不用乘2
O(√n)枚举n的因子x即可

最后一个坑点就是当n等于1的时候，这时候无论k为多少n^k都为1
所以要特判n等于1的情况

code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
int phi(int n){
    int ans=n;
    for(int i=2;i*i<=n;i++){
        if(n%i==0){
            ans=ans/i*(i-1);
            while(n%i==0)n/=i;
        }
    }
    if(n>1)ans=ans/n*(n-1);
    return ans;
}
signed main(){
    const int mod=1e9+7;
    int n,k;
    while(cin>>n>>k){
        if(n==1){
            cout<<1<<endl;
            continue;
        }
        if(k>2){
            cout<<0<<endl;
        }else if(k==2){
            cout<<1<<endl;
        }else{
            int ans=0;
            for(int i=1;i*i<=n;i++){
                if(n%i==0){
                    if(n/i!=i){
                        ans+=phi(n/i)*phi(i)*2;
                        ans%=mod;
                    }else{
                        ans+=phi(n/i)*phi(n/i);
                        ans%=mod;
                    }
                }
            }
            cout<<ans<<endl;
        }
    }
    return 0;
}

---

UVA11426 GCD - Extreme (II)

题意：

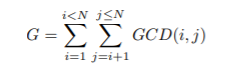
思路:

因为题目中有两个sigma，想办法把它拆开
设f(n)=gcd(1,n)+gcd(2,n)+…gcd(n-1,n) ;这是把第二个sigma的j固定为n之后第一个sigma的值
则G(n)=f(2)+f(3)+…f(n) ; 这是题目要求的G
显然G函数满足前缀和性质，因此很好处理
所以这题主要问题是在求f函数上

设g(x,n)=k，则g(x/k,n/k)=1，因此满足条件的k有phi(n/k)个则f(n)+=phi(n/k)*k
所以对于某一个n，O(√n)枚举n的因子k即可求出f(n)

但是如果对于每一个n=1,2,3…我们都这样算，显然超时
一个好的办法就是利用埃筛的思想，对于每一个数k，把k的所有倍数n加上phi(n/k)*k
详见代码

求出f()之后对其求前缀和即为G()，对于每个输入的n，可以做到O(1)输出结果

ps:
总结：多个sigma可以尝试拆开，其中某些sigma可能可以变成上一个sigma的前缀和

code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxm=4e6+5;
int phi[maxm];
int f[maxm];
void init(){//预处理欧拉函数
    for(int i=1;i<maxm;i++){
        phi[i]=i;
    }
    for(int i=2;i<maxm;i++){
        if(phi[i]==i){
            for(int j=i;j<maxm;j+=i){
                phi[j]=phi[j]/i*(i-1);
            }
        }
    }
}
void init2(){//预处理f[]
    for(int i=1;i<maxm;i++){
        for(int j=i+i;j<maxm;j+=i){
            f[j]+=phi[j/i]*i;
        }
    }
    for(int i=3;i<maxm;i++){//f[]的前缀和即G[]
        f[i]+=f[i-1];
    }
}
signed main(){
    init();
    init2();
    int n;
    while(cin>>n&&n){
        cout<<f[n]<<endl;
    }
    return 0;
}

---

bzoj2818 Gcd

题意：

给n，求有多少对x,y
1<=x,y<=n满足gcd(x,y)是素数

思路：

考虑每一个质数p对答案的贡献
gcd(x,y)=p，则gcd(x/p,y/p)=1
因为x,y<=n，所以x/p,y/p<=n/p
设a=x/p,b=y/p，则问题即求gcd(a,b)=1且1<=a,b<=n/p
因此答案就是遍历小于等于n的每个p，求出1<=a,b<=n/p中gcd(a,b)=1的对数

那么怎么求1<=x<=n中互质对数呢？
其实就是phi数组的前n项前缀和
但是因为(a,b)!=(b,a) (a!=b)，也就是数对有序，所以a!=b的时候答案要乘2，
a=b的时候不用乘2，a=b的情况只有一种：(1,1)
设phi的前缀和数组为sum，则对于每个p的答案为sum(n/p)*2+1
遍历n以内的所有素数p，ans+=sum(n/p)*2+1即可

可以优化一下空间，不用sum数组直接在phi数组上求前缀和，即phi[i]+=phi[i-1]

code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxm=1e7+5;
int notprime[maxm];
int prime[maxm],cnt;
int phi[maxm];
void init(int n){
    phi[1]=1;
    for(int i=2;i<=n;i++){
        if(!notprime[i]){
            prime[cnt++]=i;
            phi[i]=i-1;
        }
        for(int j=0;j<cnt;j++){
            if(prime[j]*i>n)break;
            notprime[prime[j]*i]=1;
            phi[prime[j]*i]=phi[i]*(i%prime[j]?prime[j]-1:prime[j]);
            if(i%prime[j]==0)break;
        }
    }
    for(int i=1;i<=n;i++){//直接在原数组上求前缀和
        phi[i]+=phi[i-1];
    }
}
signed main(){
    int n;
    cin>>n;
    init(n);
    int ans=0;
    for(int j=0;j<cnt;j++){
        ans+=phi[n/prime[j]]*2-1;
    }
    cout<<ans<<endl;
    return 0;
}

---