浅水系统-赤道Rossby&Kelvin波解

浅水方程

浅水方程是对于真实大气流体的简化模拟，然而，尽管它很简单，但它通常可以很好地洞察许多大气
波现象。 浅水模型的基本假设是：

• 流体是不可压缩的，密度为常数
• 流体足够浅，水平动量部分与高度无关
• 流体是静力的，垂直方向的加速度被忽略

假设的原因：
1、流体是不可压缩的 (Incompressible Flow)：

物理角度：对于大气或海洋中的大部分波动现象来说，流体的密度变化相对较小，可以忽略不计。因此，假设流体是不可压缩的可以简化问题，因为密度在空间和时间上的变化可以忽略。
数学角度：不可压缩流体的控制方程组更简单，其中速度场的散度为零。这使得求解流体运动方程变得更加容易。

2、流动足够浅以至于水平速度与高度无关 (Shallow Flow)：

物理角度：在许多大气和海洋波动中，垂直尺度相对于水平尺度来说较小。因此，可以假设流体是浅的，即垂直尺度远小于水平尺度，从而使得水平速度与高度无关。
数学角度：在浅水近似下，流体的运动方程可以被简化为一维或二维形式，而不需要考虑垂直方向的运动。

3、流体是静水压力的 (Hydrostatic Flow)：

物理角度：大气或海洋中的垂直加速度通常相对较小，因此可以忽略垂直方向上的动量变化，即认为流体处于静水压力的状态。
数学角度：在静水压力的假设下，流体运动方程可以被简化为更简单的形式，使得求解问题变得更加容易。

首先，考虑一个水平动量方程和静力方程：

$$\begin{array}{rlr}\frac{\partial u}{\partial t}+(\mathbf{v}\cdot \nabla )u& =& -\frac{1}{\rho }\frac{\partial p}{\partial x}+fv\\ \frac{\partial v}{\partial t}+(\mathbf{v}\cdot \nabla )v& =& -\frac{1}{\rho }\frac{\partial p}{\partial y}-fu\\ \frac{1}{\rho }\frac{\partial p}{\partial z}& =& -g,\end{array}$$

进一步考虑一个连续性方程：

$$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathbf{v})=0.$$

对从高度 z 到流体顶部的流体静力学方程进行积分可得出
（假设那里的压力消失）

$$\begin{array}{rcl}{\int }_z^{h(x,y,t)}\frac{\partial p}{\partial z}dz& =& -{\int }_z^{h(x,y,t)}\rho gdz\\ -p(x,y,z,t)& =& -\rho g[h(x,y,t)-z].\end{array}$$

则水平压强梯度力可以表达为：

$$\begin{array}{rcl}-\frac{1}{\rho }\frac{\partial p}{\partial x}& =& -g\frac{\partial h}{\partial x}=-\frac{\partial \Phi }{\partial x}\\ -\frac{1}{\rho }\frac{\partial p}{\partial y}& =& -g\frac{\partial h}{\partial y}=-\frac{\partial \Phi }{\partial y}\end{array},$$

做出以下定义：

$$\begin{array}{r}\Phi (x,y,t)=gh(x,y,t)\end{array}$$

因此，请记住，有水平速度不依赖于垂直方向并忽略科里奥利
项与垂直速度成正比，水平运动方程可以写成：

$$\begin{array}{rlrlr}\frac{\partial u}{\partial t}+(\mathbf{v}\cdot \nabla )u& & =& & -\frac{\partial \Phi }{\partial x}+fv\\ \frac{\partial v}{\partial t}+(\mathbf{v}\cdot \nabla )v& & =& & -\frac{\partial \Phi }{\partial y}-fu,\end{array}$$

上述两个方程中的独立变量数量减少到3个，（$u，v, \Phi $）,所以，如果我们有其他的方程只包含上述三个变量的，那么这个系统就完整了。

还记得连续性方程吗：

$$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathbf{v})=0.$$

这可以通过简化连续性方程和垂直积分来实现。 首先，我们注意到由于 $\rho =const$，连续性方程减少简化为：

$$\frac{\partial w}{\partial z}=-\nabla \cdot \mathbf{v}.$$

然后将其从 $0$ 到 $h(x,y,t)$ 进行垂向积分，得到：

$$\begin{array}{rcl}\int_0^h\frac{\partial w}{\partial z}~dz

&=&-\int_0^h\nabla\cdot\mathbf{v}~dz\w(h):=&\frac{dh}{dt}&=&\frac{\partial h}{\partial t}+\mathbf{v}\cdot\nabla h=-(\nabla\cdot\mathbf{v})h\end{array}$$

或者简化得到：

$$\frac{\partial \Phi }{\partial t}+\mathbf{v}\cdot \nabla \Phi =-\Phi \nabla \cdot \mathbf{v}.$$

以上，为 $(u,v,\Phi )$ 建立一组完整的微分方程，并且称为浅水方程。

赤道 $\beta$ 平面线性化

一般来说，$\beta$ 平面假设的状态为：

$$f=2|\omega |\sin \varphi \approx f_0+\beta y$$

其中，$\sin \varphi$ 是对于给定的纬度$\varphi$，通过泰勒级数展开的线性近似，因此，

$$\beta =2|\omega |\cos {\varphi }_0/a$$

其中， a表示地球的半径，如果我们假定$f_0=0$， 则 $f\approx \beta y$

$$\begin{array}{rlr}\frac{\partial u^{\prime }}{\partial t}& =& -\frac{\partial {\Phi }^{\prime }}{\partial x}+\beta y{v}^{\prime }\\ \frac{\partial v^{\prime }}{\partial t}& =& -\frac{\partial {\Phi }^{\prime }}{\partial y}-\beta y{u}^{\prime }\\ \frac{\partial {\Phi }^{\prime }}{\partial t}& =& -g{h}_e\left(\frac{\partial u^{\prime }}{\partial x}+\frac{\partial v^{\prime }}{\partial y}\right),\end{array}$$

其中带引号的变量表示来自基本状态的扰动。 这是我们用于研究赤道的基本线性方程组（具有可变系数！）波动力学。 通过调整刻度高度 $h_e$，他也可以将海洋的case包括。

讨论热带外情况下的惯性重力波和近似值 $f=$ $f_0= const, $ 并假设 $u^{\prime }(x,t),v^{\prime }(x,t),{\Phi }^{\prime }(x,t).$

赤道Rossby 和 Rossby-Gravity 模态

为了找到以下线性方程组的解，

$$\begin{array}{rlr}\frac{\partial u^{\prime }}{\partial t}& =& -\frac{\partial {\Phi }^{\prime }}{\partial x}+\beta y{v}^{\prime }\\ \frac{\partial v^{\prime }}{\partial t}& =& -\frac{\partial {\Phi }^{\prime }}{\partial y}-\beta y{u}^{\prime }\\ \frac{\partial {\Phi }^{\prime }}{\partial t}& =& -g{h}_e\left(\frac{\partial u^{\prime }}{\partial x}+\frac{\partial v^{\prime }}{\partial y}\right),\end{array}(1)$$

做出如下假设：

$$(\begin{array}{c}{u}^{\prime }\\ v^{\prime }\\ {\Phi }^{\prime }\end{array})=\left[\begin{array}{c}\hat{u}(y)\\ \hat{v}(y)\\ \hat{\Phi }(y)\end{array}\right]e^{i(kx-\nu t)}(2)$$

通过假设y方向的依赖性可以分离，我们可以将问题分解为在x方向上的波动（由$e^{i(kx-\nu t)}$表示）和y方向上的结构（由$u^{\prime }(y)$,$v^{\prime }(y)$,${\Phi }^{\prime }(y)$表示）。

这种分离的假设在数学上使问题更加可解，因为它将偏微分方程系统分解为一系列更简单的一维问题。这种分离也与物理上的一些观察相符合，例如，在一些波动现象中，波的特征可能在某个方向上变化迅速，在另一个方向上变化缓慢。

具体来说，这种分离假设在解决波动方程系统时允许我们首先解决一维问题，然后再将这些解组合起来以获得整体系统的解。这种分离的假设大大简化了解决复杂波动系统的数学和计算问题的复杂性，使我们能够更有效地理解和预测波动现象。

将方程组(2)带入到(1),得到一组关于y的常微分方程组：

$$\begin{array}{rlrl}-i\nu \hat{u}& =& -ik\hat{\Phi }+\beta y\hat{v}& (3)\\ -i\nu \hat{v}& =& -\frac{\partial \hat{\Phi }}{\partial y}-\beta y\hat{u}& (4)\\ -i\nu \hat{\Phi }& =& -g{h}_e\left(ik\hat{u}+\frac{\partial \hat{v}}{\partial y}\right).& (5)\end{array}$$

如果，方程(3)的解为：

$$\hat{u}=k/\nu \hat{\Phi }+i\beta y\hat{v}/\nu$$

将其带入方程(4),(5),得到：

$$\begin{array}{rlrl}({\beta }^2{y}^2-{\nu }^2)\hat{v}& =& ik\beta y\hat{\Phi }+i\nu \frac{\partial \Phi }{\partial y}& (6)\\ ({\nu }^2-g{h}_e{k}^2)\hat{\Phi }+i\nu g{h}_e\left(\frac{\partial \hat{v}}{\partial y}-\frac{k}{\nu }\beta y\hat{v}\right)& =& 0.& (7)\end{array}$$

最终，方程(7)可以被带入到方程(6)来消除$\Phi$,最终得到一个二阶单一未知数的微分方程：

$$\frac{{\partial }^2\hat{v}}{\partial y^2}+\left[\left(\frac{{\nu }^2}{g{h}_e}-k^2-\frac{k}{\nu }\beta \right)-\frac{{\beta }^2{y}^2}{g{h}_e}\right]\hat{v}=0.(8)$$

为了寻求该方程的 $\hat{v}$ 经向分布的解，需要满足扰动场在$|y|\to \infty$时快速消失的边界条件。

这个边界条件是必要的，因为近似值 $f\approx \beta y$ 对纬度远超过 $\pm 30°$ 时是无效的，因此如果方程要存在解，则必须被在赤道附近存在，也就是说被赤道所trapped。

公式(8) 根据 $y$ 中谐振子的经典方程有所不同，因为系数方括号不是常数，而是 $y$ 的函数。 对于足够小的 $y$ 这系数为正，解在 $y$ 上振荡，而对于大 $y$，解在 $y$ 上增长/衰退。

然而，只有衰减解才能满足边界状况。

事实证明，方程(8)的解满足一个远离赤道衰减的条件，仅当系数的常数部分为平方时才存在括号满足关系（这也是色散/频散关系！）

$$\begin{array}{rl}\frac{\sqrt{g{h}_e}}{\beta }\left(-\frac{k}{\nu }\beta -k^2+\frac{{\nu }^2}{g{h}_e}\right)& =2n+1;n=0,1,2,......\end{array}(9)$$

这是一个三次色散方程，用于确定纬向波数 $k$ 和赤道俘获自由振荡的经向模态数 $n$ 之间的关系. 如果将 $y$ 替换为无量纲的经向坐标：
$$\xi ={\left(\frac{\beta }{\sqrt{g{h}_e}}\right)}^{1/2}y(10)$$
那么，结合方(9-10)方程(8)会变为：

$$\frac{{\partial }^2\hat{v}}{\partial {\xi }^2}+\left(2n+1-{\xi }^2\right)\hat{v}=0(11)$$

这是量子力学简谐振子的微分方程。 该解具有以下形式:

$$\hat{v}(\xi )=H_n(\xi )e^{-{\xi }^2/2}(12)$$

其中 $H_n(xi)$ 表示第 $n$ 个 $Hermite$ 多项式。 这些多项式中可以表示为：

$$H_0=1,H_1(\xi )=2\xi ,H_2(\xi )=4{\xi }^2-2.(13)$$

因此， $n$ 对应于域 $|y|<\infty .$ 中经向速度剖面中的节点数。 将方程(12)插入方程(11)。 方程(11)导出 Hermite 多项式的定义微分方程之一。 一般来说，方程有三个解。方程(9)可以解释为向东和向西移动的赤道俘获重力波和向西移动的赤道罗斯贝波。

$n=0$ 的情况（经向速度扰动具有以赤道为中心的高斯分布）必须单独处理。 在这种情况下，频散关系方程(9)（这类似于一个特征方程，它给出了$\nu (k)$依赖性，

$$\left(\frac{\nu }{\sqrt{g{h}_e}}-\frac{\beta }{\nu }-k\right)\left(\frac{\nu }{\sqrt{g{h}_e}}+k\right)=0(14)$$

我们可以从中导出相速度因子为根 :

$$\nu /k=-\sqrt{g}\overline{h_e}(15)$$

对应于向西传播的重力波，由于方程中括号中的第二项是不允许的。 当方程式(14) 被明确假设不会消失。

方程(14)中括号中第一项给出的根:

$$\nu =k\sqrt{g{h}_e}\left[\frac{1}{2}\pm \frac{1}{2}{\left(1+\frac{4\beta }{k^2\sqrt{g{h}_e}}\right)}^{1/2}\right](16)$$

正根对应于向东传播的赤道惯性重力波，而负根对应于向西传播的波，对于长纬向尺度 $k\to 0$ 类似于惯性重力波，对于纬向尺度类似于罗斯贝波 天气尺度扰动的尺度特征。 这种模式通常被称为罗斯比重力波。

赤道Kelvin 波

除了上一节讨论的模式外，还有另一种赤道模式波，具有重要的现实意义。 对于这种模式，称为赤道开尔文波，经向速度扰动消失，方程如下所示：

$$\begin{array}{rcl}-i\nu \hat{u}& =& -ik\hat{\Phi }\\ \beta y\hat{u}& =& -\frac{\partial \hat{\Phi }}{\partial y}\\ -i\nu \hat{\Phi }& =& -g{h}_e\left(ik\hat{u}\right)\end{array}$$

利用上一节同样的方法，计算可以看到开尔文波色散方程是浅水重力波的方程

$$c^2={\left(\frac{\nu }{k}\right)}^2=g{h}_e$$

其中，相速度c可以是正也可以是负；而其经向结构为：

$$\beta y\hat{u}=-c\frac{\partial \hat{u}}{\partial y},$$

可以积分以得到：

$$\hat{u}=u_0{e}^{-\beta y^2/(2c)}$$

其中，$u_0$是赤道处扰动纬向速度的幅度,表明如果存在远离赤道衰减的解，则相位速度必须为正 (c > 0)。 因此开尔文波向东传播并且具有随纬度变化呈高斯分布的纬向速度和位势扰动函数，并以赤道为中心。 e 衰减幅度由下式给出:

$$Y_K=|2c/\beta {|}^{1/2},$$

对于一个相速度c为30m/s时，则对应的$Y_k=1600km$,

开尔文模式的经向力平衡是纬向速度和经向压力梯度之间的精确地转平衡。 正是赤道处科里奥利参数符号的变化使得这种特殊类型的赤道模态得以存在。

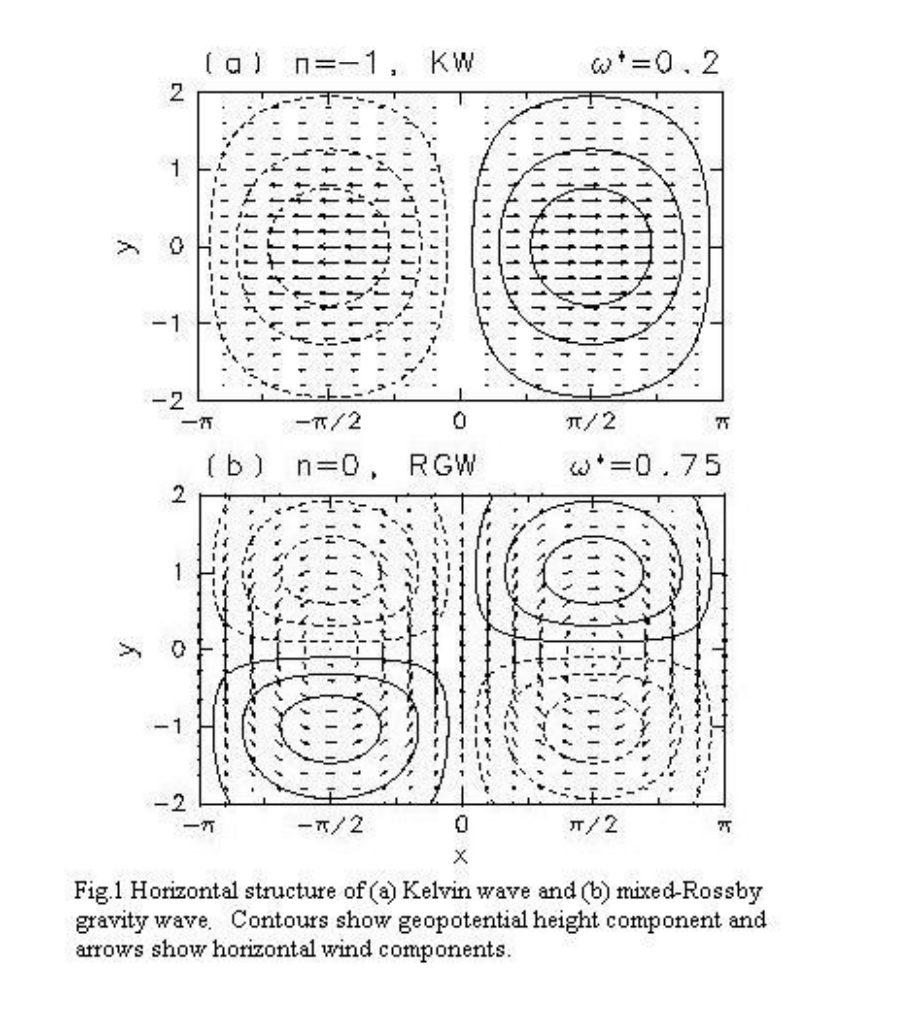
Illustration of Kelvin (upper panel) and Rossby-gravity (lower panel)
waves.

封面来源：https://www.science.org/doi/10.1126/science.aaq0469