分类问题：Logistic回归算法

分类问题

---

Logistic回归算法

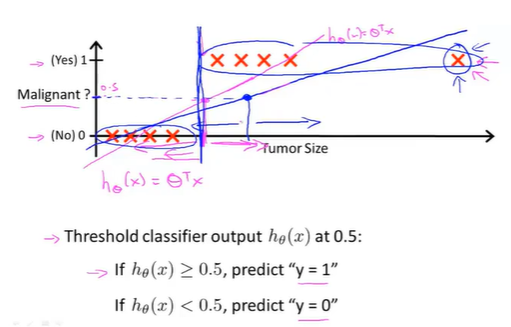
如果使用直线来拟合数据的话，我们将分类器输出阈值设为0.5，若$h_{\theta }(x)⩾0.5$，则可以预测$y=1$，否则认为$y=0$。但是如果我们再训练集中再添加一个Tumor Size很大的点，再运行线性回归我们会得到另一条直线去拟合数据，此时如果再选择0.5作为阈值则分类结果不理想。所以线性回归通常不是解决分类问题的好方法。

当面对一个分类问题时，我们应该如何选择假设方程？

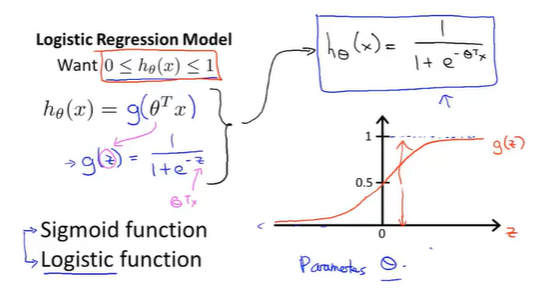
在logistic回归模型中我们通常将假设函数定义为$h_{\theta }(x)=g({\theta }^{T}x)$，其中$g$是关于$z$的函数：$g(z)=\frac{1}{1+e^{-z}}$，称为logistic函数或sigmoid函数。由此我们可以得到假设函数的形式为：$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$。有logistic函数的图像可以看出，其定义域为($-\infty$,$+\infty$)值域为(0,1)，因此假设函数$h_{\theta }(x)$的值就一定在0和1之间。

决策界限(decision boundary)

上面我们知道了logistic回归的假设函数形式，那么这个假设函数在何时会预测$y=1$，何时预测$y=0$呢？具体地说，这个假设函数输出的是给定$x$和参数$\theta$时，$y=1$的估计概率。因此我们可以设定当$h_{\theta }(x)⩾0.5$时认为$y=1$，否则认为$y=0$。

由sigmoid函数图像可以看出，当$z⩾0$时，$g(z)⩾0.5$，即${\theta }^{T}x⩾0$时，$h_{\theta }(x)⩾0.5$，此时我们预测$y=1$。

例如，假设我们已经拟好了参数$\theta =[-3,1,1{]}^T$，由上述可知，当假设函数$h_{\theta }(x)\ge 0.5$，即${\theta }^{T}x\ge 0$时，我们可以预测$y=1$，所以只要任何一个$x$满足等式$x_1+x_2\ge 3$，那么我们就能预测$y=1$。

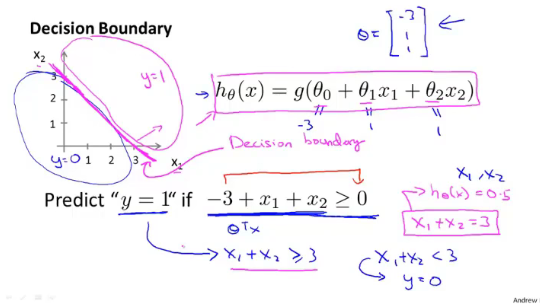
其中$x_1+x_2=3$这条直线也就是决策边界，他将整个平面分成了两部分，其中一片区域假设函数预测$y=1$，另一区域预测$y=0$。

决策边界是假设函数的一个属性，他包括参数${\theta }_0,{\theta }_1,{\theta }_2$，在上图例子中我们给出了一个训练集，但是即使我们去掉这个数据集，这条决策边界以及我们预测的$y=1$和$y=0$的区域，他们都是假设函数的属性，决定于其参数，与具体的数据集无关。只要我们有具体的参数$\theta$，我们就将完全确定决策边界。

如何拟合Logistic回归模型中参数$\theta$的值？

在线性回归中，我们定义代价函数$J(\theta )=\frac{1}{2m}{\sum }_{i=1}^m{\left(h_{\theta }\left(x^i\right)-y^i\right)}^2$，但是在Logistic回归模型中假设函数的形式为$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$，此时将其代入代价函数中，得到的代价函数是一个非凸函数，存在多个局部最优解（如下图左），此时若运行梯度下降算法计算代价函数的最小值，那么很可能得不到全局最优解。因此我们需要另外找一个代价函数来保证利用梯度下降法能够找到全局最小值。

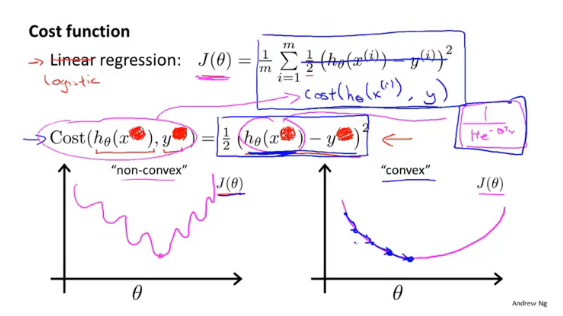
下面是我们针对Logistic回归模型定义的代价函数$Cost(h_{\theta }(x),y)$（注意：代价函数是为了根据训练集的数据来找到代价最小时的参数$\theta$，因此关于$x,y$的值都是训练集中已经给出的，我们要做的是找到合适的$\theta$来拟合数据。）

如果$y=1$时：

如果$y=0$时：

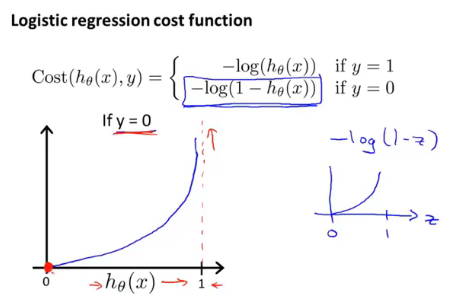
下面我们使用稍微简单一点的方法来写代价函数来替换上面的写法。这个式子是根据统计学中的极大似然估计得到的。

根据这个代价函数，我们要找出使得$J(\theta )$取得最小值的参数$\theta$。如果我们试着减小代价函数$j(\theta )$的取值，我们将得到某组参数$\theta$，最后，如果给我们一个新的样本具有某些特征值$x$，我们就可以用拟合训练样本的参数$\theta$来输出这种预测。此外，假设函数输出的取值$h_{\theta }(x)$实际上就是$y=1$的概率。

接下来要做的就是弄清楚如何最小化代价函数$J(\theta )$，这样我们才能为训练拟合出参数$\theta$。

最小化代价函数$J(\theta )$使用的是梯度下降法：

这里的$\frac{1}{m}$是常数，应该可以并入到学习率$\alpha$里面，最后得到的代价函数为：

我们可以看到Logistic回归的代价函数和线性回归的代价函数式子是完全一样的，但是我们要注意的是，Logistic回归算法中的假设函数$h_{\theta }(x)$的定义发生了变化。因此，即使更新参数的规则看起来基本相同，但由于假设函数的定义不同，所以他和线性回归的梯度下降实际上是两个完全不同的东西。

多元分类：一对多

下面就是一个多元分类的例子，我们要做的就是把这个训练集转化为三个独立的二元分类问题。

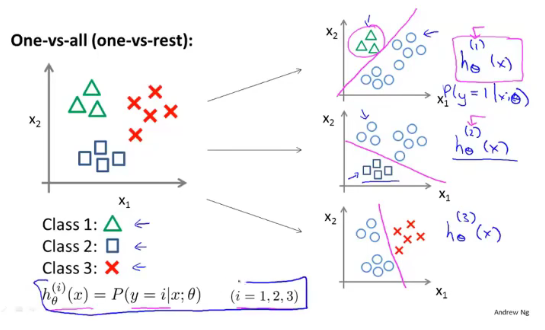
实际上每个分类器$h_{\theta }^{(i)}(x)$计算的是正类别的概率，例如第二个分类器将正方形作为正类别，那么$h_{\theta }^{(2)}(x)$的值就等于给定$x$和$\theta$时，$y=2$的概率。