sklearn 朴素贝叶斯
学习自:link
统计知识
贝叶斯学派思想为:后验概率=先验概率+数据
实际问题种想得到后验概率。先假设先验分布的模型,如正太分布,beta分布等(这个假设没有特定的依据)。
条件独立公式:
P
(
X
,
Y
)
=
P
(
X
)
P
(
Y
)
P(X,Y)=P(X)P(Y)
P(X,Y)=P(X)P(Y)
条件概率公式:
P
(
Y
∣
X
)
=
P
(
X
,
Y
)
P
(
X
)
=
P
(
X
∣
Y
)
P
(
Y
)
P
(
X
)
P(Y|X)=\frac{P(X,Y)}{P(X)}=\frac{P(X|Y)P(Y)}{P(X)}
P(Y∣X)=P(X)P(X,Y)=P(X)P(X∣Y)P(Y)
全概率公式:
P
(
X
)
=
∑
k
P
(
X
,
Y
=
y
k
)
=
∑
k
P
(
X
∣
Y
=
y
k
)
P
(
Y
=
y
k
)
P(X)=\sum_k P(X,Y=y_k)=\sum_k P(X|Y=y_k)P(Y=y_k)
P(X)=∑kP(X,Y=yk)=∑kP(X∣Y=yk)P(Y=yk)
其中,
∑
k
P
(
Y
=
y
k
)
=
1
\sum_k P(Y=y_k)=1
∑kP(Y=yk)=1.
从而可以从条件概率公式+全概率公式中推导出贝叶斯公式:
P
(
Y
=
y
i
∣
X
)
=
P
(
X
∣
Y
=
y
i
)
P
(
Y
=
y
i
)
∑
k
P
(
X
∣
Y
=
y
k
)
P
(
Y
=
y
k
)
P(Y=y_i|X)=\frac{P(X|Y=y_i)P(Y=y_i)}{\sum_k P(X|Y=y_k)P(Y=y_k)}
P(Y=yi∣X)=∑kP(X∣Y=yk)P(Y=yk)P(X∣Y=yi)P(Y=yi)
朴素贝叶斯
这个过程来自西瓜书,感觉更好理解。
(个人感觉,当一个在自己脑子中已经很直观的结论,被一个数学过程严格推导出来,会觉得很奇怪…)
第一步,最小化风险推导出优化目标:
λ
i
j
\lambda_{ij}
λij是将真实标记为
c
j
c_j
cj的样本误分类为
c
i
c_i
ci的概率。
p
(
c
i
∣
x
)
p(c_i|x)
p(ci∣x)是后验概率,也就是给定样本x,该样本分类是
c
i
c_i
ci的概率。
将样本x误分类为 c i c_i ci所产生的期望损失是: R ( c i ∣ x ) = ∑ j = 1 N λ i j P ( c j ∣ x ) R(c_i|x)=\sum_{j=1}^{N}\lambda_{ij}P(c_j|x) R(ci∣x)=∑j=1NλijP(cj∣x)
我们的任务当然是找到学习准则
h
:
X
→
Y
h:\mathcal{X}\to \mathcal{Y}
h:X→Y最小化总体风险:
R
(
h
)
=
E
x
[
R
(
h
(
x
)
∣
x
)
]
R(h)=E_x[R(h(x)|x)]
R(h)=Ex[R(h(x)∣x)]
如果对每个样本x,h能最小化上面的期望损失
R
(
h
(
x
)
∣
x
)
R(h(x)|x)
R(h(x)∣x),则总体风险也将被最小化。【这句话我的理解是,假设样本是独立荣分布的,那么每一个样本对应的损失也是独立的,互不干扰,且计算方式一致。那最小化总体风险就只需最小化每个样本的风险】
将损失
λ
i
j
\lambda_{ij}
λij取为0,1损失。
则
R
(
c
i
∣
x
)
=
∑
j
=
1
N
λ
i
j
P
(
c
j
∣
x
)
=
∑
j
=
1
,
j
≠
i
N
P
(
c
j
∣
x
)
=
1
−
P
(
c
i
∣
x
)
R(c_i|x)=\sum_{j=1}^{N}\lambda_{ij}P(c_j|x)=\sum_{j=1,j \neq i}^{N}P(c_j|x)=1-P(c_i|x)
R(ci∣x)=∑j=1NλijP(cj∣x)=∑j=1,j=iNP(cj∣x)=1−P(ci∣x)
综上,优化目标是:
arg min
c
∈
Y
R
(
c
∣
x
)
=
arg max
c
∈
Y
P
(
c
∣
x
)
\argmin_{c\in \mathcal{Y}} R(c|x) = \argmax_{c\in \mathcal{Y}} P(c|x)
c∈YargminR(c∣x)=c∈YargmaxP(c∣x)
显然,这也符合直观,我们就是要找到使得后验概率最大的类别作为学习器的输出。
估计后验概率 P ( c ∣ x ) P(c|x) P(c∣x)
现实任务中无法直接获得后验概率
P
(
c
∣
x
)
P(c|x)
P(c∣x)。使用贝叶斯公式估计:
P
(
c
∣
x
)
=
P
(
c
)
P
(
x
∣
c
)
P
(
x
)
P(c|x)=\frac{P(c)P(x|c)}{P(x)}
P(c∣x)=P(x)P(c)P(x∣c)
其中
P
(
c
)
P(c)
P(c)是先验概率;
P
(
x
∣
c
)
P(x|c)
P(x∣c)是样本x相对于类标记c的类条件概率。
P©通过训练集里,类别c的比例估计。
P(x|c)通过训练集里,取值为x的样本在类别c样本中的比例估计。但是,问题来了:
现实中,x的所有取值的可能性往往比样本数都大,很有可能出现”未被观测到的情况“。
解决办法:”属性条件独立性假设"
P
(
c
∣
x
)
=
P
(
c
)
P
(
x
∣
c
)
P
(
x
)
=
P
(
c
)
P
(
x
)
Π
i
=
1
d
P
(
x
i
∣
c
)
P(c|x)=\frac{P(c)P(x|c)}{P(x)}=\frac{P(c)}{P(x)}\Pi_{i=1}^{d}P(x_i|c)
P(c∣x)=P(x)P(c)P(x∣c)=P(x)P(c)Πi=1dP(xi∣c)
具体地,
P
(
c
)
=
∣
D
c
∣
∣
D
∣
P(c)=\frac{|D_c|}{|D|}
P(c)=∣D∣∣Dc∣
P
(
x
i
∣
c
)
=
∣
D
c
,
x
i
∣
∣
D
c
∣
P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|}
P(xi∣c)=∣Dc∣∣Dc,xi∣ (离散属性)
P
(
x
i
∣
c
)
=
1
2
π
σ
c
,
x
i
exp
(
−
(
x
i
−
μ
c
,
x
i
)
2
2
σ
c
,
x
i
2
)
P(x_i|c)=\frac{1}{\sqrt{2\pi}\sigma_{c,x_i}}\exp(-\frac{(x_i-\mu_{c,x_i})^2}{2\sigma^2_{c,x_i}})
P(xi∣c)=2πσc,xi1exp(−2σc,xi2(xi−μc,xi)2) (连续属性,假设了该属性变量服从正太分布)
…不写算法具体过程了…
贝叶斯求解过程不涉及求导与矩阵运算,效率很高。
sklearn朴素贝叶斯类库
三种:sklearn.naive_bayes.GaussianNB、MultinomialNB、BernoulliNB
先验分别是:高斯分布、多项式分布、伯努利分布
使用场景分别是:样本特征大部分是连续值、多元离散值、二元离散值
sklearn.naive_bayes.GaussianNB
官方:link
参数相对其他分类器比较少。
class sklearn.naive_bayes.GaussianNB(*, priors=None, var_smoothing=1e-09)
参数:
priors: array-like of shape (n_classes,) 类别的先验概率。一经指定,不会根据数据进行调整。
var_smoothing: float, default=1e-9 所有特征的最大方差部分,添加到方差中用于提高计算稳定性。
方法:
partial_fit(X, y[, classes, sample_weight]) 对一批样本进行增量拟合
假设先验概率是正太分布:
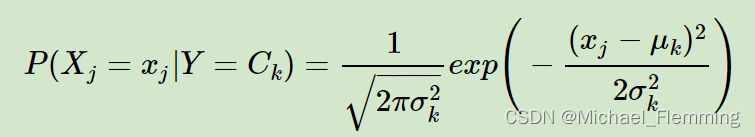
其中,
μ
k
\mu_k
μk和
σ
k
\sigma_k
σk是需要从训练集估计的值。
预测有三种办法:predict,predict_log_proba和predict_proba
# 我还是想用鸢尾花的数据集试一下,特征的变量都是连续的,是分类问题
import numpy as np
from sklearn.datasets import load_iris
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
iris_data = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, random_state=20, test_size=0.3)
# 创建学习器对象
gau_bay = GaussianNB()
gau_bay.fit(X_train, y_train) # 拟合
x_new = X_test[0, :]
print(gau_bay.predict(x_new[np.newaxis, :]))
print(gau_bay.predict_proba(x_new.reshape(1, -1)))
print(gau_bay.predict_log_proba(x_new[np.newaxis, :]))
MultinomialNB
class sklearn.naive_bayes.MultinomialNB(*, alpha=1.0, fit_prior=True, class_prior=None)

参数:
alpha: float, default=1.0 附加的(Laplace/Lidstone)平滑参数(0表示不平滑)
fit_prior: bool, default=True 是否学习类别先验概率。如果为False,将使用统一的先验。
class_prior: array-like of shape (n_classes,), default=None类别的先验概率。一经指定先验概率不能随着数据而调整
BernoulliNB
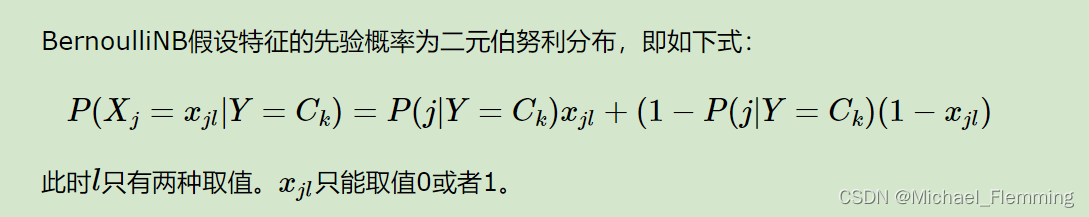






















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








