初级算法3_逻辑回归

1 逻辑回归

1.1 逻辑回归原理

理想的替代函数应当预测分类为0或1的概率，当为1的概率大于0.5时，判断为1，当为1的概率小于0.5时，判断为0。因概率的值域为$[0,1]$，这样的设定比线性回归合理很多。
常用的替代函数为Sigmoid函数，即：
$$h(z)=\frac{1}{1+e^{-z}}$$ 其中，$z={\theta }^{T}x$
我们可以看到，当z大于0时，函数大于0.5；当函数等于0时，函数等于0.5；函数小于0时，函数小于0.5。如果用函数表示目标分到某一类的概率，我们可以采用以下“单位阶跃函数”来判断数据的类别：
$$h(z)=\{\begin{array}{rlr}0，& & z<0\\ 0.5，& & z=0\\ 1，& & z>0\end{array}$$
若Z大于0，则判断为正例；若小于0，判断为反例；若等于0，可任意判别。由于Sigmoid函数单调且可导，函数在（0，1）之间程Z字型，可以很好的模拟二分类情况，因此很适合我们要解决的问题。

1.2 逻辑回归损失函数推导及优化

$$\begin{gathered} P(y=1|x;\theta )=h_{\theta }(x) \\ P(y=0|x;\theta )=1-h_{\theta }(x) \end{gathered}$$ 可以写作一般公式，
$$P(y|x;\theta )=h(x{)}^y(1-h(x){)}^{(1-y)}$$ 极大似然函数为，
$$L(\theta )=\prod _{i=1}^m{h}_{\theta }(x^{(i)}{)}^{y^{(i)}}(1-h_{\theta }(x^{(i)}{)}^{(1-y^{(i)})}$$ 对数极大似然函数为，
$$l(\theta )=logL(\theta )=\sum _{i=1}^m{y}^{(i)}log{h}_{\theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))$$ 损失函数为,
$$J(\theta )=-\frac{1}{m}l(\theta )=-\frac{1}{m}\sum _{i=1}^m{y}^{(i)}{h}_{\theta }(x^{(i)})+(1-y^{(i)})(1-h_{\theta }(x^{(i)}))$$ 损失函数表示了预测值和真实值之间的差异程度，预测值和真实值越接近，则损失函数越小。

• 我们使用梯度下降法求解
  $$\theta :=\theta -\alpha {\Delta }_{\theta }J(\theta )=\theta +\frac{\alpha }{m}{\Delta }_{\theta }l(\theta )$$ 由于$g_{\theta }^{\prime }(z)=g_{\theta }(z)(1-g_{\theta }(z))$
  因此可以求得，
  $$\begin{gathered} \frac{\partial J(\theta )}{\partial {\theta }_i}=\frac{1}{m}\sum _{i=1}^m{y}^{(i)}\frac{1}{h_{\theta }(x^{(i)})}{h}_{\theta }(x^{(i)})(1-h_{\theta }(x^{(i)}))x^{(i)}+(1-y^{(i)})\frac{1}{1-h_{\theta }(x^{(i)})}{h}_{\theta }(x^{(i)})(h_{\theta }(x^{(i)})-1) \\ =\frac{1}{m}\sum _{i=1}^m{y}^{(i)}(1-h_{\theta }(x^{(i)}))x^{(i)}+(y^{(i)}-1)h_{\theta }(x^{(i)})x^{(i)}=\frac{1}{m}\sum _{i=1}^m(y^{(i)}-h_{\theta }(x^{(i)}))x^{(i)} \end{gathered}$$ 可以看到，形式和线性回归很相似，这是因为他们都属于广义线性模型

1.3 正则化与模型评估指标

1.3.1 正则化

我们可以在损失函数后面，加上正则化函数，即 𝜃 的惩罚项，来抑制过拟合问题。

• L1正则
  $$J(\theta )=\frac{1}{m}\sum _{i=1}^m{y}^{(i)}{h}_{\theta }(x^{(i)})+(1-y^{(i)})(1-h_{\theta }(x^{(i)}))+\frac{\lambda }{m}\sum _{i=1}^m|{\theta }_i|$$ $${\Delta }_{{\theta }_i}l(\theta )=\frac{1}{m}\sum _{i=1}^m(y^{(i)}-h_{\theta }(x^{(i)}))x^{(i)}+\frac{\lambda }{m}sgn({\theta }_i)$$ 梯度下降法的迭代函数变为,
  $$\theta :=\theta -K^{\prime }(\theta )-\frac{\lambda }{m}sgn(\theta )$$ $K(\theta )$为原来的损失函数，由于最后一项的符号由$\theta$决定，可以看到，当$\theta$大于零时，更新后的$\theta$变小；当$\theta$小于零时，更新后的$\theta$变大。因此，L1正则化调整后的结果会更加稀疏（结果向量中有更多的0值）。

• L2正则
  $$J(\theta )=\frac{1}{m}\sum _{i=1}^m{y}^{(i)}{h}_{\theta }(x^{(i)})+(1-y^{(i)})(1-h_{\theta }(x^{(i)}))+\frac{\lambda }{2m}\sum _{i=1}^m{\theta }_i^2$$ $${\Delta }_{{\theta }_i}l(\theta )=\frac{1}{m}\sum _{i=1}^m(y^{(i)}-h_{\theta }(x^{(i)}))x^{(i)}+\frac{\lambda }{m}{\theta }_i$$ 梯度下降法的迭代函数变为,
  $$\theta :=\theta -K^{\prime }(\theta )-\frac{2\lambda }{m}\theta$$ $K(\theta )$为原来的损失函数，最有一项的$\lambda$决定了对参数的惩罚力度，惩罚力度越大，最后的结果向量的参数普遍较小且分散，避免了个别参数对整个函数起较大的影响。

1.3.2 评价指标

由于逻辑回归模型属于分类模型，不能用线性回归的评价指标。 二元分类的评价指标基本都适用于逻辑回归。 观察以下混淆矩阵，

我们可以用查准率和查全率来评价预测结果：

• 查准率 $P=\frac{TP}{TP+FP}$
• 查全率 $R=\frac{TP}{TP+FN}$

我们可以用P-R曲线表示查准率和查全率之间的关系：

查准率和查全率经常相互矛盾，一般查准率高时查全率低，查全率高时查准率低。我们经常针对具体的应用场景决定更看重哪一个指标。
P-R曲线越靠外，则预测效果越好，如果两条P-R曲线相交，则难说孰优孰率，可以计算曲线包住的面积。
我们可以用$F_{\beta }$表达对查准率/查全率的不同偏好，定义为：
$$F_{\beta }=\frac{(1+{\beta }^2)\cdot P\cdot R}{({\beta }^2\cdot P)+R}$$ $\beta$大于1时，查全率有更大影响；$\beta$小于1时，查准率有更大影响；$\beta$等于0时，即标准的F1度量。
但是，当正负样本分布发生变化时，P-R曲线会受到较大影响。试想负样本的数量扩大10倍，FP和TN都会成倍增加，会影响到查准率和查全率。这时候我们可以用ROC曲线来评价模型。
定义：

• $TPR=\frac{TP}{TP+FN}$
• $FPR=\frac{FP}{TN+FP}$

绘图的过程可以将样本的预测概率排序，将分类阈值从最小向最大移动，则每个阈值会得到一组TPR和FPR的位置点，将所有的点连结，则绘制成ROC曲线，同时，计算曲线下的面积，即AUC值。AUC值越大，则说明预测的效果越好。

• AUC值的计算
  计算方法一：
  
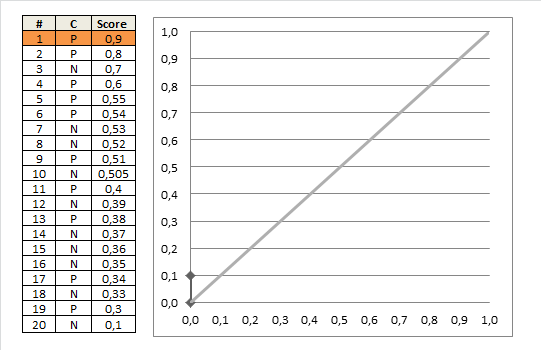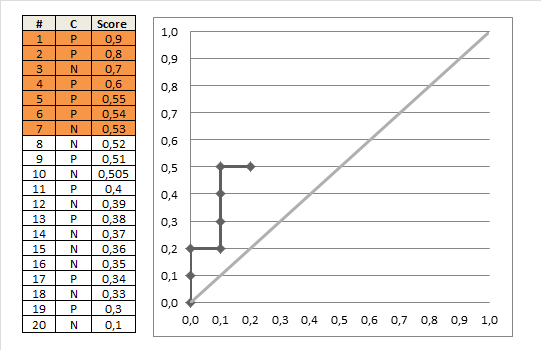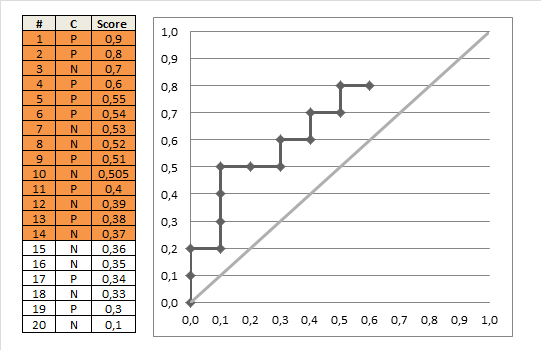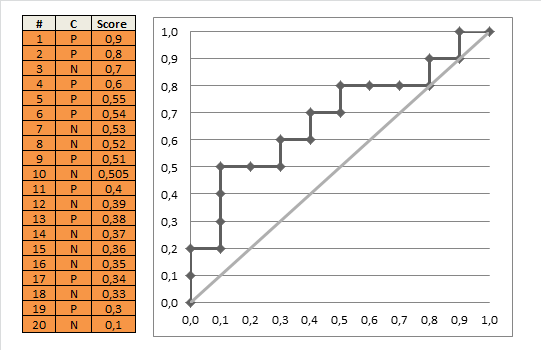
  上图很形象地描述了RUC的描绘过程，那么，计算AUC值也很直观了，每一组点的坐标,可以写成$(x_i,y_i)$，那么，
  $$AUC=\frac{1}{2}\sum _{i=1}^{m-1}(x_{i+1}-x_i)\cdot (y_i+y_{i+1})$$ 上式乘以二分之一的原因是，阈值变更时，上图正例和反例单个出现的，但当数据量增加，每个阈值同时存在多个正例和反例时，上升的轨迹可能是斜线，因此要计算梯形面积。

  计算方法二：
  任意给一个正样本和负样本，如果正样本的预测概率大于负样本，意味着以此正样本的预测概率为阈值，预测是成功的，则增加1分；如果两者相等，则增加0.5分。
  $$令AU{C}_{ij}=\{\begin{array}{rlrlr}1,& & if& & pos\_scor{e}_i>neg\_scor{e}_j\\ 0.5,& & if& & pos\_scor{e}_i=neg\_scor{e}_j\\ 0,& & if& & pos\_scor{e}_i<neg\_scor{e}_j\end{array}$$ 单个正样本对所有负样本的得分占全部负样本的比例为：$AU{C}_i=\frac{1}{m^{-}}{\sum }_{j=1}^{m^{-}}AU{C}_{ij}$
  如果一个正样本在ROC曲线上的坐标为$(x,y)$，x即排序在其之前的负样本所占的比例，即假正例率。那么，整条曲线的ROC值即
  $$AUC=\frac{1}{m^{+}{m}^{-}}AU{C}_{ij}=\frac{1}{m^{+}{m}^{-}}\sum _{x^{+}\in D^{+}}\sum _{x^{-}\in D^{-}}(\mathbb{I}(f(x^{+})<f(x^{-}))+\frac{1}{2}\mathbb{I}(f(x^{+})=f(x^{-}))$$ 方法一是将每个预测概率预测正确的比例做积分，方法二是将每个正样本的预测概率大于负样本预测概率的比例做积分。
  我们可以把方法1理解为，将ROC曲线看作y = f(x)，求定积分${\int }_0^{1}f(x)dx$，方法2理解为，将RUC曲线看作是x = g(y),求${\int }_0^{1}g(y)dy$。

1.4 逻辑回归优缺点

• 优点：从上面介绍已经可以额看到，逻辑回归的思想简洁，可以很好的解决二问题。
• 缺点：
  观察下图
  
  第一，预测结果呈Z字型（或反Z字型），因此当数据集中在中间区域时，对概率的变化会很敏感，可能使得预测结果缺乏区分度。
  第二，由于逻辑回归依然是线性划分，对于非线性的数据集适应性弱。
  第三，当特征空间很大，性能欠佳。
  第四，只能处理两分类问题。

1.5 样本不均衡问题

每200封邮件里有1封垃圾邮件，当碰到一封新邮件时，我们只需将其预测为正常邮件，可以达到99.5%的准确率。但是这样的学习器毫无价值，因为他无法判断出任意一封垃圾邮件。
我们预测时，实际上是用预测出的概率值与一个阈值进行比较，例如当y > 0.5时，判断为正例。$\frac{y}{1-y}$表示了正例可能性和反例可能性的比值。阈值为0.5时，即$\frac{y}{1-y}>1$时，预测为正例。
如果令$m_{+}$为样本正例数，$m_{-}$为样本负例数，随机的观测几率为$\frac{m_{+}}{m_{-}}$。只要分类器的预测概率高于观测几率，应判定为正例，即
$$\frac{y}{1-y}>\frac{m_{+}}{m_{-}}，预测为正例$$ 这时候，需要对预测值进行调整，使得$\frac{y^{\prime }}{1-y^{\prime }}=\frac{y}{1-y}\cdot \frac{m_{+}}{m_{-}}$，那么，0.5的阈值依然是合理的分类决策。
这就是类别不平衡的一个基本策略——“再缩放”。
“再缩放”的三类做法：

• 欠采样：去除一些反例使得正反例数目接近。
• 过采样：增加一些正例使得正反例数目接近。
• 阈值移动：基于原始集学习，当在预测是，将决策阈值改为符合样本正负样本比例的值。

可以想到，过采样因为增加了数据，时间开销大于欠采样法。但欠采样法由于随机丢弃反例，可能丢失一些重要信息。这时候可以将反例划分成若干个集合分别学习，从全局来看并非丢失重要信息。

2 代码实现

2.1 调用sklearn的线性回归模型训练数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

%matplotlib inline

df_X = pd.read_csv('./logistic_x.txt', sep='\ +',header=None, engine='python') #读取X值
ys = pd.read_csv('./logistic_y.txt', sep='\ +',header=None, engine='python') #读取y值
ys = ys.astype(int)
df_X['label'] = ys[0].values #将X按照y值的结果一一打标签

ax = plt.axes()
#在二维图中描绘X点所处位置，直观查看数据点的分布情况
df_X.query('label == 0').plot.scatter(x=0, y=1, ax=ax, color='blue')
df_X.query('label == 1').plot.scatter(x=0, y=1, ax=ax, color='red')

结果：

#提取用于学习的数据
Xs = df_X[[0, 1]].values
Xs = np.hstack([np.ones((Xs.shape[0], 1)), Xs]) 
ys = df_X['label'].values

from __future__ import print_function
import numpy as np
from sklearn.linear_model import LogisticRegression

lr = LogisticRegression(fit_intercept=False) #因为前面已经将截距项的值合并到变量中，此处参数设置不需要截距项
lr.fit(Xs, ys) #拟合
score = lr.score(Xs, ys) #结果评价
print("Coefficient: %s" % lr.coef_)
print("Score: %s" % score)

结果：

Coefficient: [[-1.70090714  0.55446484  1.07222372]]
Score: 0.898989898989899

ax = plt.axes()

df_X.query('label == 0').plot.scatter(x=0, y=1, ax=ax, color='blue')
df_X.query('label == 1').plot.scatter(x=0, y=1, ax=ax, color='red')

_xs = np.array([np.min(Xs[:,1]), np.max(Xs[:,1])])

#将数据以二维图形式描点，并用学习得出的参数结果作为阈值，划分数据区域
_ys = (lr.coef_[0][0] + lr.coef_[0][1] * _xs) / (- lr.coef_[0][2])
plt.plot(_xs, _ys, lw=1)

结果：

2.2 用梯度下降法将相同的数据分类

class LGR_GD():
    def __init__(self):
        self.w = None 
        self.n_iters = None
    def fit(self,X,y,alpha=0.03,loss = 1e-10): # 设定步长为0.002，判断是否收敛的条件为1e-10
        [m,d] = np.shape(X) #自变量的维度
        self.w = np.zeros(d) #将参数的初始值定为0
        tol = 1e5
        self.n_iters = 0
        #============================= show me your code =======================
        while tol > loss: #设置收敛条件
            for i in range(d):
                temp = y - X.dot(self.w)
                self.w[i] = self.w[i] + alpha *np.sum(temp * X[:,i])/m
            
            tol = np.abs(np.sum(y -  X.dot(self.w)))
            self.n_iters += 1 #更新迭代次数
         #============================= show me your code =======================
    def predict(self, X):
        # 用已经拟合的参数值预测新自变量
        y_pred = X.dot(self.w)
        return y_pred  

if __name__ == "__main__":
    lr_gd = LGR_GD()
    lr_gd.fit(Xs,ys)

    ax = plt.axes()

    df_X.query('label == 0').plot.scatter(x=0, y=1, ax=ax, color='blue')
    df_X.query('label == 1').plot.scatter(x=0, y=1, ax=ax, color='red')
    print(lr_gd.n_iters)
    
    _xs = np.array([np.min(Xs[:,1]), np.max(Xs[:,1])])
    _ys = (lr_gd.w[0] + lr_gd.w[1] * _xs) / (- lr_gd.w[2])
    plt.plot(_xs, _ys, lw=1)

2.3 用牛顿法实现结果

class LGR_NT():
    def __init__(self):
        self.w = None
        self.n_iters = None
    def fit(self,X,y,loss = 1e-10): # 判断是否收敛的条件为1e-10
        y = y.reshape(-1,1) #重塑y值的维度以便矩阵运算
        [m,d] = np.shape(X) #自变量的维度
        self.w = np.zeros((1,d)) #将参数的初始值定为0
        tol = 1e5
        n_iters =0
        Hessian = np.zeros((d,d))
        #============================= show me your code =======================
        while tol > loss:
            zs = X.dot(self.w.T)
            h_x = 1 / (1 + np.exp(-zs))
            grad = np.mean(X*(y - h_x),axis=0)
            for i in range(d):
                for j in range(d):
                    if j>=i:
                        Hessian[i][j] = np.mean(h_x*(h_x-1)*X[:,i]*X[:,j]) #更新海森矩阵中的值
                    else:
                        Hessian[i][j] = Hessian[j][i] #按海森矩阵的性质，对称点可直接得出结果
            theta = self.w - np.linalg.inv(Hessian).dot(grad)
            tol = np.sum(np.abs(theta - self.w))
            self.w = theta
            n_iters += 1
        #============================= show me your code =======================
        self.w = theta
        self.n_iters = n_iters
        
    def predict(self, X):
        # 用已经拟合的参数值预测新自变量
        y_pred = X.dot(self.w)
        return y_pred  

if __name__ == "__main__":
    lgr_nt = LGR_NT()
    lgr_nt.fit(Xs,ys)
print("梯度下降法结果参数：%s;梯度下降法迭代次数：%s" %(lgr_gd.w,lgr_gd.n_iters))
print("牛顿法结果参数：%s;牛顿法迭代次数：%s" %(lgr_nt.w,lgr_nt.n_iters))

结果：

梯度下降法结果参数：[[-2.62051144  0.7603715   1.17194673]];梯度下降法迭代次数：32590
牛顿法结果参数：[[-2.6205116   0.76037154  1.17194674]];牛顿法迭代次数：47