图形排版问题

题目描述：

        输入一个高度为h，输出一个高为h，上底边为h的梯形。

输入：

        一个整数h（1<=h<=1000）。

输出：

        h所对应的梯形

样例输入：

        4

样例输出：

            ****

         ******

      ********

   **********

 ​​​​​​第0行h个*，第 i 行h+2i个*，最后一行（第h-1行）h+2(h-1)=3h-2个*。 

第 i 行空格的个数：一行的最大*数-第i行的*数=h+2(h-1)-(h+2i)=2h-2i-2。

 代码如下：

#include<iostream>
using namespace std;

int main(){
    int h;
    while(cin>>h){
        for(int i=0;i<h;i++){
            for(int j=0;j<3*h-2;j++){
                if(j<2*h-2*i-2){
                    cout<<" ";
                }else{
                    cout<<"*";
                }
            }
            cout<<endl;
        }
    }
    return 0;
}

 运行结果如下图所示：

 题目描述：

        输入n值，输入上底为n，高是n的一半的等腰实心梯形

输入样例：5

输出样例：

         *****

        *******

      *********

分析如下：

1、梯形的高度h=round(n/2)（#include<cmath>）->图形的行数为h

2、首行有n个*，下一行总比上一行多两个*，故第i行有n+2*(i-1)个*

3、最后一行中*的数量决定了图像的列数->列数为n+2*(h-1)

4、空格数是列数与该行中*数量之差即n+2*(h-1)-(n+2*(i-1))=2*(h-i) 

代码如下：

#include<iostream>
#include<cmath>
using namespace std;

int main(){
    int i,j;
    double n;
    cin>>n;
    double h=round(n/2);
    for(i=1;i<=h;i++){//round(x):四舍五入
        for(j=2*(h-i);j>0;j--){
            cout<<" ";
        }
        for(j=n+2*(i-1);j>0;j--){
            cout<<"* ";
        }
        cout<<endl;
    }
    return 0;
}

运行结果如下图所示： 

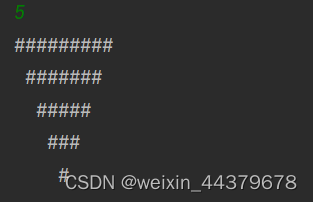
题目描述：输出一个n层的倒三角

分析如下：

1、图形的行数row=n个#

2、第一行中#的数量决定了图像的列数->列数col=1+2*(n-1)

代码如下：

#include<iostream>
using namespace std;

int main(){
    int n;
    while(cin>>n){
        int row=n;
        int col=1+2*(n-1);
        for(int i=row;i>=1;i--){
            for(int j=1;j<=col;j++){
                if(j<= n-i || j>col-(n-i)){
                    cout<<" ";
                }else{
                    cout<<"#";
                }
            }
            cout<<endl;
        }
    }
    return 0;
}