求最短路径之弗洛伊德Floyd算法

1. 弗洛伊德Floyd算法介绍

Floyd算法又称为插点法，是一种用于寻找给定的加权图中多源点之间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。注意这个可不是心理学的那个弗洛伊德。

是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题。

算法的时间复杂度为O(N3)，空间复杂度为O(N2)。

优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单。

缺点：时间复杂度比较高，不适合计算大量数据。

2. 核心思路

通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。

从图的带权邻接矩阵A=[a(i,j)] n×n开始，递归地进行n次更新，即由矩阵D(0)=A，按一个公式，构造出矩阵D(1)；又用同样地公式由D(1)构造出D(2)；……；最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵，同时还可引入一个后继节点矩阵path来记录两点间的最短路径。

采用的是(松弛技术)，对在i和j之间的所有其他点进行一次松弛。所以时间复杂度为O(n^3);

其状态转移方程如下： map[i,j]:=min{map[i,k]+map[k,j],map[i,j]}

map[i,j]表示i到j的最短距离，K是穷举i,j的断点，map[n,n]初值应该为0.当然，如果这条路没有通的话，还必须特殊处理，比如没有map[i,k]这条路

3. 算法原理
Floyd算法的原理是动态规划。

设Di,j,k为从i到j的只以(1…k)集合中的节点为中间节点的最短路径的长度。

1.  若最短路径经过点k，则Di,j,k = Di,k,k − 1 + Dk,j,k − 1；
   

2.  若最短路径不经过点k，则Di,j,k = Di,j,k − 1。
   

因此，Di,j,k = min(Di,k,k − 1 + Dk,j,k −1,Di,j,k − 1)。

Floyd-Warshall算法的描述如下：

for k ← 1 to n do

fori ← 1 to n do

for j ← 1 to n do

 if (Di,k + Dk,j < Di,j) then

   Di,j ← Di,k + Dk,j; 

其中Di,j表示由点i到点j的代价，当Di,j为 ∞ 表示两点之间没有任何连接。

4. 图解法

如下图1所示

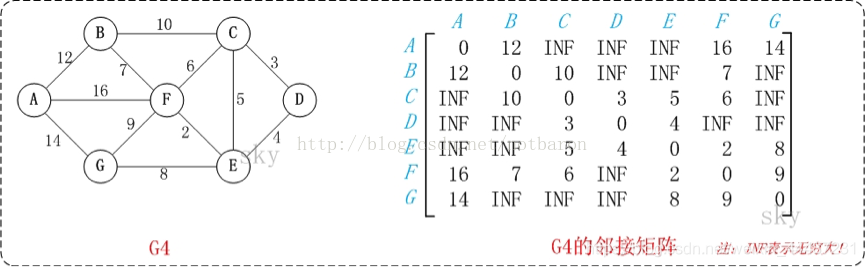
点与点之间的举例用矩阵来表示。INF表示点之间不连通。

具体步骤如下图2,3

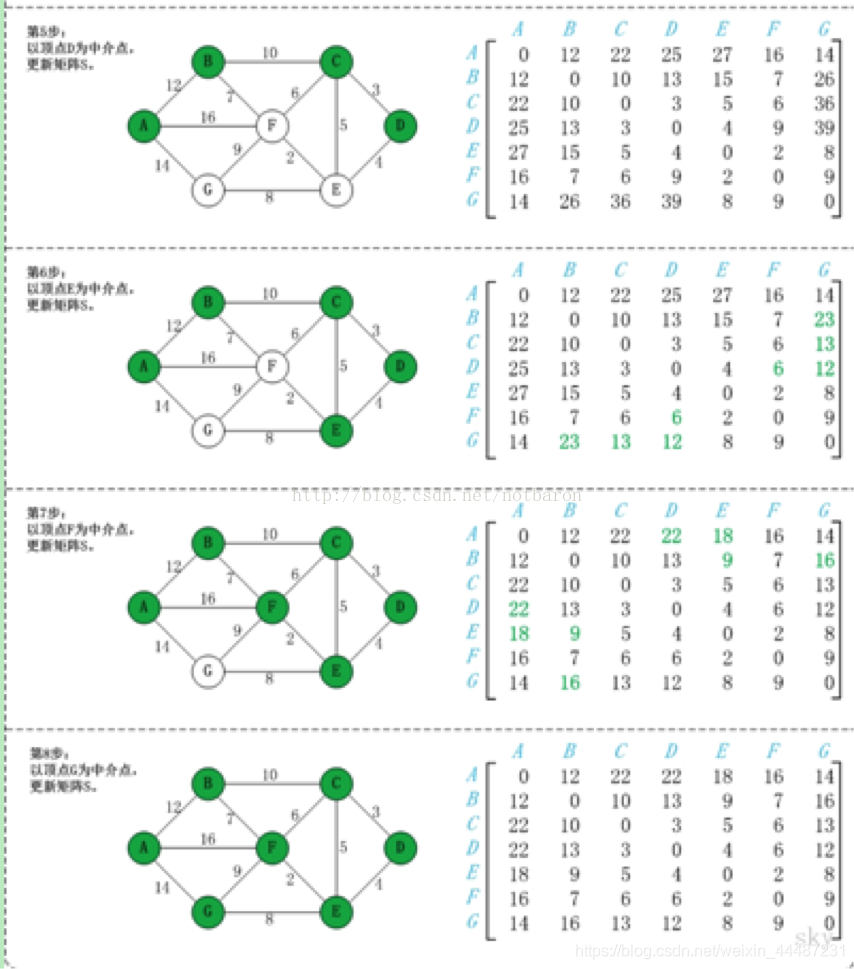
初始状态：S是记录各个顶点间最短路径的矩阵。
第1步：初始化S。

矩阵S中顶点a[i][j]的距离为顶点i到顶点j的权值；如果i和j不相邻，则a[i][j]=∞。实际上，就是将图的原始矩阵复制到S中。
注:a[i][j]表示矩阵S中顶点i(第i个顶点)到顶点j(第j个顶点)的距离。

第2步：以顶点A(第1个顶点)为中介点，若a[i][j]> a[i][0]+a[0][j]，则设置a[i][j]=a[i][0]+a[0][j]。
以顶点a[1]6，上一步操作之后，a[1][6]=∞；而将A作为中介点时，(B,A)=12，(A,G)=14，因此B和G之间的距离可以更新为26。

同理，依次将顶点B,C,D,E,F,G作为中介点，并更新a[i][j]的大小。

5. 代码实现

输入两个参数赋值给n和m.

m值表示输入m个值的数量。

N表示输入矩阵的大小。

将任何两个点间的最大距离设置成无限大。

输入m数值，3个值，前两个表示坐标，后一个表示值。

（如 1 0 12 表示a[1][0]=12,表示第1个点到第0个点的权值是12）

然后将矩阵 a和矩阵的对角线清零。

其中矩阵a是初始化的图，所有直接相连的顶点才有权值。

矩阵d是不断更新的图，会计算当前最新的顶点与顶点之间的最小权值，默认是所有都是无限大。

然后循环判断a[i][k]+a[k][j]<d[i][j]，如果成立说明i和j两点之间有更短路径可达，则更新d矩阵，如果该值小于a矩阵的值，a矩阵也需要更新。

最后如下图所示（是图解法中的输入，顶点0 ，1,2,3,4,5,6分别表示顶点A,B,C,D,E,F,G）

6. 源码

#include<stdio.h>

#include<stdlib.h>

#definemax1000000000;

int a[1000][1000],d[1000][1000];

int main(){

           inti,j,k,m,n;

           intx,y,z;

 

           printf("inputthe numbers you should to storage\n");

           scanf("%d",&m);

           printf("inputthe scale of your matrix\n");

           scanf("%d",&n);

           for(i=0;i<n;i++)

                     for(j=0;j<n;j++){

                     a[i][j]=max;

           }

           for(i=0;i<m;i++){

                     scanf("%d%d%d",&x,&y,&z);

                     a[x][y]=z;

                     a[y][x]=z;

           }

           for(i=0;i<n;i++)

                     for(j=0;j<n;j++)

                                d[i][j]=max;

           for(i=0;i<n;i++){

                                d[i][i]=0;

                                a[i][i]=0;

           }

 

           for(k=0;k<n;k++)

                     for(i=0;i<n;i++)

                                for(j=0;j<n;j++){

                                          if(a[i][k]+a[k][j]<d[i][j]){

                                                     d[i][j]=a[i][k]+a[k][j];

                                                     if(a[i][j] > d[i][j] )

                                                               a[i][j]= d[i][j];

                                          }

                                }

 

           printf("inputthe node a & node b\n");

           scanf("%d%d",&n,&m);

           printf("%d",d[n][m]);

           return0;

}