【论文精读】Differential Representations for Mesh Processing（微分坐标在网格处理用的应用）

Abstract

曲面表示和处理是计算机图形学和几何建模中的关键问题之一，因为它极大地影响了可能的应用范围。在本文中，我们将介绍与拉普拉斯处理框架和微分表示相关的几何处理的最新进展。该框架基于定义在多边形网格上的线性算子，并提供了各种处理应用，如形状逼近和紧凑表示、网格编辑、水印和变形。该框架的核心是基于网格拉普拉斯算子的微分坐标定义和高效网格几何表示的新基。

Introduction

表明：本文的论述是基于拉普拉斯框架和微分坐标的网格处理和建模。
研究的基础在于网格的微分性质，微分性质是由在网格上定义的某些线性算子派生的（微分坐标）。这种方法提供了用新基表示表面的方法，
与全局的笛卡尔坐标表示法不同，微分曲面表示包括有关表面的局部形状、局部细节的大小和方向的信息。

拉普拉斯算子和曲面的微分表示

基本定义

给定三角曲面$V=(V,E,F)$分别是顶点、边、面。顶点数据是定义在笛卡尔坐标系下的，${\mathbf{v}}_i=(x_i,y_i,z_i)$。
微分坐标表示：

其中 N ( i ) = { j ∣ ( i , j ) ∈ E } N(i) =\{j |(i, j)∈E\} N(i)={j∣(i,j)∈E} ，同时$d_i=|N(i)|$是i的近邻个数(i的度或价).
绝对笛卡尔坐标下向量到δ坐标下向量的变换可以用矩阵的形式表示。
设A为网格的邻接(连通性)矩阵:
令$D$为对角矩阵使$D_{ii}=d_i$。然后矩阵将绝对坐标转换成相对坐标:

考虑L矩阵的对称形式，通常更方便地定义为$L_s=DL=D-A$，

笛卡尔坐标和微分坐标之间的转换关系是：
$$\begin{gathered} L_s\mathbf{x}=D{\delta }^{(x)} \\ {L}_s\mathbf{y}=D{\delta }^{(y)} \\ {L}_s\mathbf{z}=D{\delta }^{(z)} \end{gathered}$$
例子：

矩阵$L_s$(或$L$)称为网格的拓扑(或图)拉普拉斯。图拉普拉斯在代数和图论中得到了广泛的研究，主要是因为它们的代数性质与它们所表示的图的组合性质有关.

**拓展：从微分几何的角度来看

δ坐标可以看作是连续拉普拉斯-贝尔特拉米算子（Laplace–Beltrami operator）的离散化，如果我们假设我们的网格M是光滑表面的分段线性近似。我们可以把顶点$v_i$处的微分坐标向量写成:
对于连续曲面而言：
$${\delta }_i=\frac{1}{|\gamma |}{\int }_{\mathbf{v}\in \gamma }({\mathbf{v}}_{\mathbf{i}}-\mathbf{v})dl(\mathbf{v})$$

其中γ是绕着vi的一个封闭简单曲面曲线，|γ |是γ的长度。
如下图：

值得注意的是，拉普拉斯函数的几何离散化具有更好的近似性质。Meyer等人建议采用由Pinkall和Polthier[6]首先提出的协切权值，而不是均匀权值:

由于π附近的余切的性质，余切权值可能是负的，对于非常大的角来说，定义余切权值是有问题的。所以产生了模仿余切权值的中值坐标：

上述的角度alpha和theta对应的图如下：

这些处理方式，在网格的过滤、编辑、压缩等应用中都有很好的应用。

δ坐标曲面重建

在下文中，我们将使用上述定义的微分曲面表示法。我们将根据手头的任务，对δ坐标进行不同的运算。任何此类操作的最后一步必须是曲面重建，或者换句话说，我们需要恢复M顶点的笛卡尔坐标。
给定一组δ坐标，我们能唯一地恢复全局坐标吗?
答案是否定的，因为矩阵L或(Ls)是对称半正定，不可求逆，解不出来。（证明略）
为了唯一的恢复全局坐标，我们需要解一个全秩的线性系统。
假设M是连通的，现在我们需要指定一个顶点的笛卡尔坐标来求解平移自由度（这里不理解的可以看原文的证明，跟为什么L不可逆有关）。

定理：
替换顶点i的坐标等价于从L中去掉第i行和第i列
这使得矩阵可逆。

通常，我们会锚定不止一个顶点的约束条件，令C是顶点索引的集合，有了额外的约束

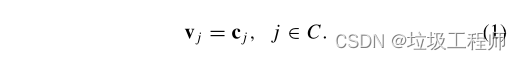
假如，锚定点的索引是{1，2，3，…，m}，那么有线性系统：

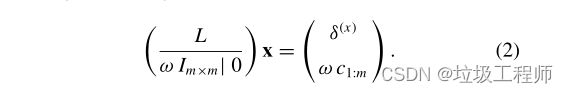
上述解释：我们在处理的时候没有使用直接将约束代入线性系统的方式，就是前面说的替换顶点坐标，而是采用了一种类似最小二乘的思路。得到一个系数矩阵$\tilde{L}$. 这样的话，我们可以保证我们锚定的每个顶点区域也是尽可能光滑的而不是完全“钉死”。但注意，在后续我们的讨论中，我们将继续将上述方式称为“位置约束”或“建模约束”，尽管它们可能不能被最小二乘解完全满足。
权重ω > 0可以用来调整位置约束的重要性【或者说软硬】(通常，每个约束都有自己的权重，我们也可以进一步在基本拉普拉斯矩阵的行上应用不同的权重)。额外的约束使我们的线性系统过度确定(方程多于未知数)，并且通常不存在精确解。然而，该系统是满秩的，因此在最小二乘意义上具有唯一解：

将上述方程用解析的最小二乘解的解公式表示，其中系统矩阵为(n + m) × n的$\tilde{L}$。

而b则是上述(2)式中的右边项$\mathbf{b}=(\delta ,w{c}_1,...,w{c}_m{)}^T$
下图是一个小栗子：

*拓展：求解速度问题

从δ坐标重建曲面的一个重要的实际方面是求解最小二乘问题(3)式的有效和精确的数值方法的可用性。
采用Cholesy分解是解决大型数据的有效方法。
因式分解需要大量的计算时间，而反替换步骤通常非常快。使用先进的线性求解器，如TAUCS库[9]，使计算非常高效。
注意，解的精度高度依赖于线性系统的条件作用。拉普拉斯矩阵是出了名的病态:当我们只添加一个锚点时，最大奇异值≈L与网格中的最大度成正比，而最小奇异值的一个很好的估计是一个顶点到单个锚点的最大拓扑距离与网格中顶点数量的乘积。。然而，在系统中加入锚点改善了系统的条件，使得常规方程的分解变得稳定。在[14]中给出了一种从下到下限定最小奇异值的严格方法;边界取决于锚点的数量和它们在网格上的间距。

总之，从全局笛卡尔表示到微分表示的转换是由一个具有局部支持的线性算子完成的:网格拉普拉斯算子。反之亦然:为了从微分表示中恢复笛卡尔坐标，需要解决一个稀疏线性最小二乘问题。

拉普拉斯矩阵的谱属性

因为拉普拉斯矩阵式对称半正定的，所以有一个标准正交的特征基（特征值组成）。
所以一些研究在于研究这个谱的性质来分析形状性质。