【概率论与数理统计 Probability and Statistics 2】—— 概率的公理化以及概率的八大性质

一、概率的公理化表述：

我们在前面的随机事件的定义都是比较口语化的：随机试验的结果就是随机事件嘛。今天我们给出公理化的定义：随机事件都要满足下面三个公理：

1. 非负性：对于任意事件 $A$，有：$0\le P(A)\le 1$；
2. 规范性：$P(\Omega )=1$；
3. 可加性：对于两两互斥的事件 $A_1,A_2,\cdots ,A_n$，有：$P({\bigcup }_{i=1}^n{A}_i)={\sum }_{i=1}^{n}P(A_i)$

二、概率的八大性质及其证明

下面是概率的八大性质以及部分证明：
【性质一】非负性：对于任意事件 $A$，有：$0\le P(A)\le 1$；

【性质二】规范性：$P(\Omega )=1$；

【性质三】可加性：若事件 $A$ 与事件 $B$ 互斥，则 $P(A+B)=P(A)+P(B)$

【性质四】$P(\Phi )=0$
$证明$：$A=A+\Phi$；因此，$P(A)=P(A+\Phi )$，又由于事件 $A$ 与空集 $\Phi$ 是互斥的，因此：$P(A)=P(A)+P(\Phi )$，故 $P(\Phi )=0$

这里补充一个小插曲：我们知道，不可能事件的概率是0，那么概率为0的事件是不是不可能事件呢？
答案是：No！！以几何概型为例，我们朝一根线段上扔一个质点，质点落在点（1，0）上的概率是0吧，因为（1，0）没有长度啊，所以概率是0，但是这件事不是不可能的噢，没准一扔刚好就是在那个（1，0）上了呢对吧。

【性质五】若：$A\subset B$，则 $P(A)\le P(B)$
$证明$：我们知道 $B=B-A+A=(B-A)+A$，那么我们发现：事件 $(B-A)$ 和事件 $A$ 是互斥事件，因此右完全可加定理【性质三】可知：$$P(B)=P(B-A)+P(A)$$
又由概率的非负性可知：$P(B-A)\ge 0$，因此得出：$P(B)\ge P(A)$

【性质六】对于任意事件，$P(A)=1-P(\bar{A})$
$证明$：由于 $A+\bar{A}=\Omega$，因此：$P(A+\bar{A})=P(\Omega )=1$，又因为 $A$ 与 $\bar{A}$ 是互斥事件，因此：$P(A)+P(\bar{A})=1$。因此：$P(A)=1-P(\bar{A})$

【性质七】对于任意事件，都有：$P(A-B)=P(A)-P(AB)$
$证明$：我们从一个新的角度去可视化理解这个证明。
我们知道任意的两个事件，无非就是三个关系—— 互斥、包含和相交。我们看看：

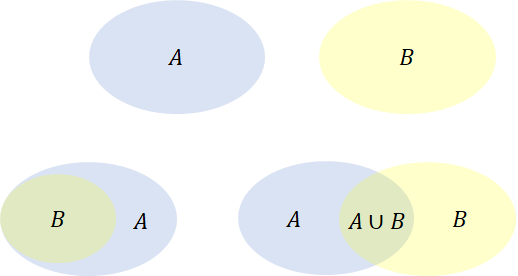
我们看看第一种：互斥的情况，假如 $A,B$ 互斥，$A-B$ 表示从 $A$ 中减去 $B$ 的部分，可是这俩事件都没有公共部分，因此 $A-B=A$，即 $P(A-B)=P(A)$，对应地，$P(AB)=0$。因此，就有：$P(A-B)=P(A)-P(AB)$

我们接着看第二个情况：包含，如果是 $A$ 包含 $B$，那么 $A-B$ 就是货真价实的从 $A$ 中减去 $B$，这是不是相当于从 $A$ 中减去 $A,B$ 的公共部分？因为 $AB=B$！也就是：$A-B=A-AB$，那么就有：$$P(A)=P(A-AB+AB)=P(A-AB)+P(AB)=P(A-B)+P(AB)$$
即：$P(A-B)=P(A)-P(B)$

我们再来看看最后一种情况：相交。这俩事件相交，那么 $A-B$ 依然表示的是从 $A$ 中减去 $B$ 的成分，而 $A$ 中 $B$ 的成分就是 $AB$！即：$A-AB=A-B$，那么$$P(A)=P(A-AB+AB)=P(A-AB)+P(AB)=P(A-B)+P(AB)$$
所以稍作变换我们就可以得出：$P(A-B)=P(A)-P(AB)$

【性质八】加法原理：对于任意的 $A,B$，$P(A+B)=P(A)+P(B)-P(AB)$
$证明$：我们知道，$A\cup B=A+B-AB$（因为 $AB$ 加多了一次，要减掉）
因此，$P(A\cup B)=P(A)+P(B-AB)$，对于 $P(B-AB)$，我们用性质七：$$P(B-AB)=P(B)-P(AB)$$
因此，我们得到：$P(A\cup B)=P(A)+P(B)-P(AB)$

扩展：（$important$）：$$P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC)$$