最后更新:2019/08/06
注意:这篇文章还没有被完成,将来可能会产生较大变动,请以最终版本为准。
线段树入门总结
之前在刷题的时候就遇到了各种各样的 n l o g n nlogn nlogn 数据结构需求,然后就在学长口中听到「这题线段树搞一搞就出来了」,然而看教程又一知半解,最近终于找了个专题把线段树学了下,发现实际还是蛮好理解的。
线段树的引入
考虑下面一道题:
1000 m s / 128 M B 1000ms / 128MB 1000ms/128MB
给定 n n n个正整数 ( 1 ≤ n ≤ 100000 ) ( 1\leq n\leq 100000) (1≤n≤100000), 编号从 1 1 1到 n n n,用 a [ i ] a[i] a[i] ( 1 ≤ i ≤ n , 1 ≤ a [ i ] ≤ 1 e 9 ) (1\leq i \leq n, 1\leq a[i] \leq 1e9) (1≤i≤n,1≤a[i]≤1e9)表示。
接下来有 m m m组查询 ( 1 ≤ m ≤ 100000 ) (1\leq m\leq 100000) (1≤m≤100000),求 a [ l ] a[l] a[l]到 a [ r ] a[r] a[r]的数字之和是多少,其中 ( 1 ≤ l ≤ r ≤ 100000 ) (1\leq l \leq r \leq100000) (1≤l≤r≤100000)。
- 我们可以通过暴力求和,或者维护前缀和数组来给出结果。(当然暴力求和会 T L E TLE TLE)
但如果在题目中增加别的需求:
1000 m s / 128 M B 1000ms / 128MB 1000ms/128MB
给定 n n n个正整数 ( 1 ≤ n ≤ 100000 ) ( 1\leq n\leq 100000) (1≤n≤100000), 编号从 1 1 1到 n n n,用 a [ i ] a[i] a[i] ( 1 ≤ i ≤ n , 1 ≤ a [ i ] ≤ 1 e 9 ) (1\leq i \leq n, 1\leq a[i] \leq 1e9) (1≤i≤n,1≤a[i]≤1e9)表示。
接下来有 m m m组操作 ( 1 ≤ m ≤ 100000 ) (1\leq m\leq 100000) (1≤m≤100000)。
操作1:求 a [ l ] a[l] a[l]到 a [ r ] a[r] a[r]的数字之和是多少,其中 ( 1 ≤ l ≤ r ≤ 100000 ) (1\leq l \leq r \leq100000) (1≤l≤r≤100000)。
操作2:将 a [ t ] a[t] a[t]增加 k k k,其中 ( 1 ≤ t ≤ 100000 , 1 ≤ k ≤ 1 e 9 ) (1\leq t \leq100000, 1\leq k \leq 1e9) (1≤t≤100000,1≤k≤1e9)。
考虑之前的两个方案:
- 如果用暴力求和,我们可以在 O ( 1 ) O(1) O(1) 的时间内进行修改,在 O ( n ) O(n) O(n) 的时间内进行求和。
- 如果维护前缀和数组,我们可以在 O ( n ) O(n) O(n) 的时间内进行修改,在 O ( 1 ) O(1) O(1) 的时间内进行求和。
无论用哪种方案,我们最终的时间复杂度都是 O ( n m ) O(nm) O(nm),其中 n n n 是数字个数, m m m 是操作次数,显然在这个环境下会 T L E TLE TLE,因此:
- 我们需要一个能够在 O ( l o g n ) O(logn) O(logn) 的时间内进行修改和查询的数据结构,也就是线段树。
线段树的原理
对于上题,我们可以把 1 1 1 到 100000 100000 100000 的区间分解成两个子区间,每个子区间记录了这个区间内部所有元素的和,反复这么操作直到最后的区间长度只有 1 1 1 为止。可以证明所有子区间的数量不超过数字数量的四倍。
由于线段树是基于二分思想构造的数据结构,在划分区间时应尽量从中间把区间分割,即计算一个 m i d = ⌊ l + r 2 ⌋ mid= \lfloor \frac{l+r}{2} \rfloor mid=⌊2l+r⌋,使得区间 [ l , r ] [l,r] [l,r] 被切割成 [ l , m i d ] [l, mid] [l,mid] 和 [ m i d + 1 , r ] [mid+1, r] [mid+1,r] 两块。
下面是一个把
1
1
1 到
13
13
13 的区间分解的例子,结合图片可以更好理解。
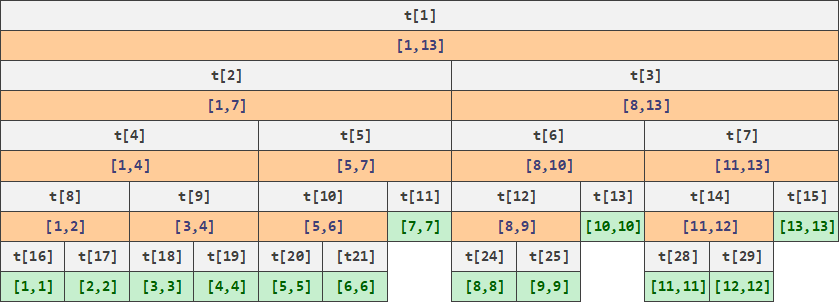
在这个数据结构下,我们有:
- 对于每个区间查询
[
l
,
r
]
[l, r]
[l,r],我们可以从这些子区间内选取一些区间合并成目标区间,这个数量是
l
o
g
log
log 级别的。
下面是一个区间查询的例子:
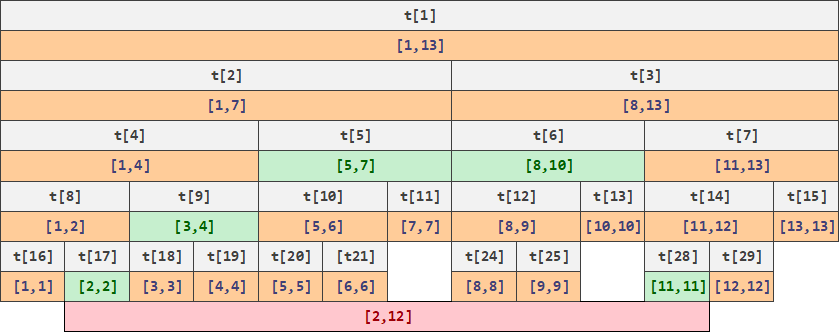
- 对于每个节点更新,我们可以自底向顶地更新所有包含该节点的区间,这个区间的数量也是
l
o
g
log
log 级别的。
下面是一个更新节点的例子:
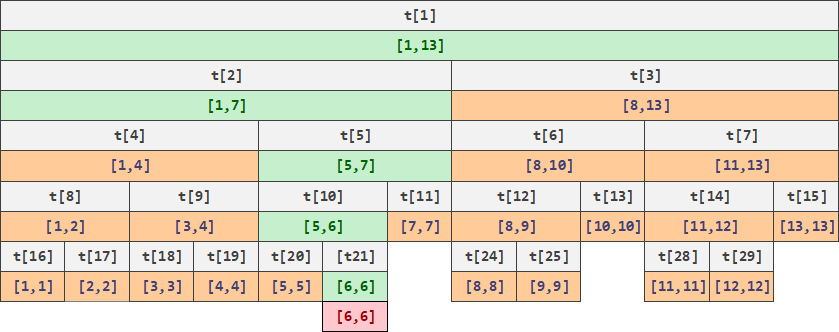
可以看到,将区间不断二分之后,树形结构带来的优势使得修改和查询都被降低在 l o g log log 级别。
线段树的实现
存储
线段树的每个节点存放了一个区间和,节点代表区间的范围可以通过递归过程计算,但为了方便理解还是用结构体进行建树。
对于每个节点,我们需要保存下面几个数值:区间的两端,以及区间所有数据和。
struct node{
int left, right;
long long val;
}t[maxn << 2]; //线段树需要四倍空间,具体证明可以百度
建树
我的习惯是从下标 1 1 1 开始建树,由于满二叉树的性质,节点 x x x 的子节点下标是 2 ∗ x 2*x 2∗x 和 2 ∗ x + 1 2*x+1 2∗x+1(当然,可能有些节点空着,没有赋值),因此我们可以写出这两个函数(你也可以写成宏定义)来增加代码可读性:
inline int left_son(int p) { return p << 1; } //位运算会比乘法稍快一点
inline int right_son(int p) { return p << 1 | 1; }
之后就是递归建树的过程了,在读取完 a [ n ] a[n] a[n] 数组之后,调用函数 b u i l d ( 1 , 1 , n ) build(1,1,n) build(1,1,n) 来建立一颗线段树。其中第一个参数代表当前节点,第二个和第三个参数代表区间范围。注意只有叶子节点在建树的时候赋值了,其他的节点都是在其所有的子节点赋值完毕后才调用 p u s h _ u p push\_up push_up 函数来赋值。
inline void push_up(int p) {
t[p].val = t[left_son(p)].val + t[right_son(p)].val; //父节点的值等于子节点值的和
}
void build(int p, int build_left, int build_right) {
//把目前节点代表的区间存储起来
t[p].left = build_left;
t[p].right = build_right;
if (build_left == build_right) {
//找到叶子节点,赋值并返回
t[p].val = a[build_left];
return;
}
int build_mid = (build_left + build_right) >> 1;
//递归建树
build(left_son(p), build_left, build_mid);
build(right_son(p), build_mid + 1, build_right);
//递归完成,子树必然赋值完成,利用push_up函数把子节点的值加起来
push_up(p);
}
下面这张图片可能会使这个过程容易理解一些:
其中上面的红色部分代表堆栈,橙色表示已经赋值完成,黄色表示正在处理,绿色表示正在赋值。

这样我们就把数据在 O ( n ) O(n) O(n) 的时间内建好了线段树。
查询
要查询某个区间的值,思路其实和建树的思路很像,调用 q u e r y ( 1 , l e f t , r i g h t ) query(1, left, right) query(1,left,right) 来获取区间和,其中第一个参数代表当前节点,第二个和第三个参数代表待查询区间的范围。当区间相等时就说明不用往下寻找。
long long query(int p, int query_left, int query_right) {
if (t[p].left == query_left && t[p].right == query_right) {
//找到了该段区间和,直接返回数值
return t[p].val;
}
if (t[left_son(p)].right >= query_right) {
//待查询区间为该节点左子树的子集
return query(left_son(p), query_left, query_right);
} else if (t[right_son(p)].left <= query_left) {
//待查询区间为该节点右子树的子集
return query(right_son(p), query_left, query_right);
} else {
//待查询区间跨越该节点左右子树
return query(left_son(p), query_left, t[left_son(p)].right) +
query(right_son(p), t[right_son(p)].left, query_right);
}
}
[需要一张gif]
这样我们就在
O
(
l
o
g
n
)
O(logn)
O(logn) 的时间内查询到了区间和。
修改
至于修改节点的值,实际上和查询的代码惊人的相似。调用 u p d a t e ( 1 , x , v a l ) update(1,x,val) update(1,x,val) 来修改指定节点,其中第一个参数代表当前节点,第二个参数代表待修改节点,第三个参数代表要增加的值。第三个参数在不同的题目中代表的意义通常是不同的。
void update(int p, int upd_p, int upd_val) {
if (t[p].left == t[p].right && t[p].left == upd_p) {
//找到了待修改节点,直接修改目标节点
t[p].val += upd_val;
}
if (t[left_son(p)].right >= upd_p) {
//目标节点在左子树里
update(left_son(p), upd_p, upd_val);
} else if (t[right_son(p)].left <= upd_p) {
//目标节点在右子树里
update(right_son(p), upd_p, upd_val);
}
//由于子节点更新了,所以父节点的值也需要更新
push_up(p);
}
我们就在 O ( l o g n ) O(logn) O(logn) 的时间内修改好了节点。
线段树的优势
到刚才为止,程序要求的操作都满足「单点修改,区间查询」的性质,而这一点树状数组也能做到,并且代码量比线段树要短很多(虽然难理解一些),线段树的优势没有体现出来。
那么看下面这道题:
1000 m s / 128 M B 1000ms / 128MB 1000ms/128MB
给定 n n n个正整数 ( 1 ≤ n ≤ 100000 ) ( 1\leq n\leq 100000) (1≤n≤100000), 编号从 1 1 1到 n n n,用 a [ i ] a[i] a[i] ( 1 ≤ i ≤ n , 1 ≤ a [ i ] ≤ 1 e 9 ) (1\leq i \leq n, 1\leq a[i] \leq 1e9) (1≤i≤n,1≤a[i]≤1e9)表示。
接下来有 m m m组操作 ( 1 ≤ m ≤ 100000 ) (1\leq m\leq 100000) (1≤m≤100000)。
操作1:求 a [ l ] a[l] a[l]到 a [ r ] a[r] a[r]的数字之和是多少,其中 ( 1 ≤ l ≤ r ≤ 100000 ) (1\leq l \leq r \leq100000) (1≤l≤r≤100000)。
操作2:将 a [ l ] a[l] a[l]到 a [ r ] a[r] a[r]增加 k k k,其中 ( 1 ≤ l ≤ r ≤ 100000 , 1 ≤ k ≤ 1 e 9 ) (1\leq l \leq r \leq100000, 1\leq k \leq 1e9) (1≤l≤r≤100000,1≤k≤1e9)。
与之前题目唯一的区别就是修改操作从一个点变成了一个区间。
考虑到线段树修改节点的复杂度为 O ( l o g n ) O(logn) O(logn),要是把每个点都修改一遍就是 O ( n l o g n ) O(nlogn) O(nlogn),那么整体复杂度就会变成 O ( m n l o g n ) O(mnlogn) O(mnlogn),甚至比暴力还要慢……
所以这肯定不是正解。我们应该操作的是区间,而不是把所有节点都跑一遍。我们已经可以在 O ( l o g n ) O(logn) O(logn) 的时间内把一个需要进行操作的区间分割成几个子区间相加,那只需要对这些子区间进行操作就可以了。
lazy标记
所有讲解线段树的文章都会提到这个玩意,因为在引入
l
a
z
y
lazy
lazy 标记之后,区间修改的复杂度被重新降为
O
(
l
o
g
n
)
O(logn)
O(logn)
具体思路就是:由于我们维护的是区间,当我们更新时,如果某个节点的区间和目标区间重合,那么我们在整个区间上打一个
l
a
z
y
lazy
lazy 标签,代表这个区间下所有元素都需要加上
l
a
z
y
lazy
lazy 标签的数值,然后就可以不用更新下面的节点。当我们在查询的时候碰到带有
l
a
z
y
lazy
lazy 标签的节点时,顺路把标记往下放就可以了。我们只会在需要用到的时候才去计算,因此这个标记十分的
“
l
a
z
y
”
“lazy”
“lazy” 。
我们在树的存储结构中加上一个 l a z y lazy lazy 标记。
struct node {
int left, right;
long long val, lazy; //懒更新标签
} t[maxn << 2];
然后引入一个下放 l a z y lazy lazy 标记的函数,它的作用是下放 l a z y lazy lazy 标记并更新子区间数值。
inline void push_down(int p) {
//如果没有标记就不做处理
if (t[p].lazy == 0) return;
if (t[p].left != t[p].right) {
//如果有子区间,那就下放标记到两个子区间
t[left_son(p)].lazy = t[p].lazy;
t[right_son(p)].lazy = t[p].lazy;
//更新子区间的数值
t[left_son(p)].val += (t[left_son(p)].right - t[left_son(p)].left + 1) * t[p].lazy;
t[right_son(p)].val += (t[right_son(p)].right - t[right_son(p)].left + 1) * t[p].lazy;
}
//清除lazy标记
t[p].lazy = 0;
}
建树的时候需要把 l a z y lazy lazy 标记赋值为0(根据题目不同可能会产生变化)。
void build(int p, int build_left, int build_right) {
t[p].left = build_left;
t[p].right = build_right;
if (build_left == build_right) {
t[p].val = a[build_left];
t[p].lazy = 0; //新添加的语句
return;
}
int build_mid = (build_left + build_right) >> 1;
build(left_son(p), build_left, build_mid);
build(right_son(p), build_mid + 1, build_right);
push_up(p);
}
查询的时候需要把有 l a z y lazy lazy 标记的节点数值顺便下放。
long long query(int p, int query_left, int query_right) {
if (t[p].left == query_left && t[p].right == query_right) {
return t[p].val;
}
push_down(p) //新添加的语句
if (t[left_son(p)].right >= query_right) {
return query(left_son(p), query_left, query_right);
} else if (t[right_son(p)].left <= query_left) {
return query(right_son(p), query_left, query_right);
} else {
return query(left_son(p), query_left, t[left_son(p)].right) +
query(right_son(p), t[right_son(p)].left, query_right);
}
}
区间修改的函数变动也不是很大。调用 u p d a t e ( 1 , l , r , v a l ) update(1,l,r,val) update(1,l,r,val) 来对整个区间进行修改,其中第一个参数代表当前节点,第二和第三个参数代表要更新的区间,第四个参数代表要加上的值(这点会根据题目不同而变得不同)。
void update(int p, int upd_left, int upd_right, int upd_val) {
if (t[p].left == upd_left && t[p].right == upd_right) {
//找到重合区间直接更新,并打上lazy标记
t[p].lazy += upd_val;
t[p].val += (t[p].right - t[p].left + 1) * upd_val;
return;
}
//下放标记
push_down(p);
if (t[left_son(p)].right >= upd_right) {
update(left_son(p), upd_left, upd_right, upd_val);
} else if (t[right_son(p)].left <= upd_left) {
update(right_son(p), upd_left, upd_right, upd_val);
} else {
update(left_son(p), upd_left, t[left_son(p)].right, upd_val);
update(right_son(p), t[right_son(p)].left, upd_right, upd_val);
}
push_up(p);
}
[需要一张gif]
由于线段树维护的是各个区间,因此操作的核心也在区间上,与其他的数据结构进行对比也可看出线段树的表现十分稳定:
| 数组 | 前缀和数组 | 树状数组1 | 线段树 | |
|---|---|---|---|---|
| 单点查询 | O ( 1 ) O(1) O(1) | O ( 1 ) O(1) O(1) | O ( l o g n ) O(logn) O(logn) | O ( l o g n ) O(logn) O(logn) |
| 区间查询 | O ( n ) O(n) O(n) | O ( 1 ) O(1) O(1) | O ( l o g n ) O(logn) O(logn) | O ( l o g n ) O(logn) O(logn) |
| 单点修改 | O ( 1 ) O(1) O(1) | O ( n ) O(n) O(n) | O ( l o g n ) O(logn) O(logn) | O ( l o g n ) O(logn) O(logn) |
| 区间修改 | O ( n ) O(n) O(n) | O ( n ) O(n) O(n) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( l o g n ) O(logn) O(logn) |
线段树的不足
相信很多人都有建树一半发现这题线段树没法维护的经历。实际上,线段树看起来很快(实际上的确如此),但有一些局限性:它的速度是基于它的 l a z y lazy lazy 标记产生的,而 l a z y lazy lazy 标记要在树上传递必须满足结合律,比如区间 m a x / m i n max/min max/min 、 s u m sum sum 、 x o r xor xor 之类的。
例题
这里顺便放点入门级的题目,以供练习。
洛谷P3372 线段树 1
HDU1754 I Hate It
HDU1166 敌兵布阵
ZOJ1610 Count the Colors
洛谷P3373 线段树 2
实际上,树状数组有多种建设方式,也有支持区间查询+区间修改的树状数组,这里按照最简单的树状数组(单点修改+区间查询)来统计性能 ↩︎






















 282
282











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








