熵权法计算权重原理&python实现

最新推荐文章于 2025-03-18 20:33:35 发布

我是女生，我不做程序媛

最新推荐文章于 2025-03-18 20:33:35 发布

阅读量1.3w

点赞数 35

分类专栏： Python 数据分析与机器学习

本文链接：https://blog.csdn.net/weixin_44644621/article/details/114038354

版权

信息熵权重熵权法 Python实现信息量

关键词由CSDN通过智能技术生成

数据分析与机器学习同时被 2 个专栏收录

23 篇文章

订阅专栏

Python

10 篇文章

订阅专栏

信息熵越大，信息量到底是越大还是越小？权重和信息熵的大小到底是正相关还是负相关？
网上有一些相反的说法。
有些说：熵越大，方差越大，包含的信息越多，权重越大。
另一些说：熵越小，不确定性越小，提供的信息越大，权重越大。
今天复盘一下熵权法计算权重的原理，并python实现。

熵权法计算权重原理

信息熵计算

熵是对混乱程度的一种度量。混乱程度越大，熵就越大，包含的信息量越大；混乱程度越小，熵就越小，包含的信息量就越小。

计算公式：
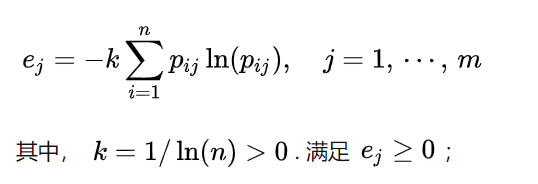
在这里插入图片描述
这里的p是指标 j 中值为 i 的样本数占总样本数量的比例。
比如，共有2个样本，当指标 j 取值分别为0,1，那么p(j=0)=1/2，p(j=1)=1/2，带入公式可得e=1。
当2个样本取值分别为1/2,1/2时，p只有一个，p(j=1/2)=1，带入公式得e=0。
由此可知，方差越大，熵越大，包含的信息越多，权重应当越大。
那么，为什么会有一些地方说，熵越小，信息量越大，权重越大呢？

熵权法计算

这个问题要从熵权法计算权重的公式说起：

归一化
对于不同量纲的指标比较信息熵显然没有意义，需要先进行归一化。
同时，需要对负向指标正向化处理，处理后的指标均为正向指标。
计算熵值

需要注意的是，这里的p不再是每个取值的数量所占的比例，而是该取值的大小除以该指标所有取值的总和。
比如，共有2个样本，当指标 j 取值分别为0,1，那么p₁=0/(0+1)，p₂=1/(0+1)，带入公式可得e=0。
当2个样本取值分别为1/2,1/2时，p₁=1/2/(1/2+1/2)=1/2，p₂=1/2/(1/2+1/2)，带入公式可得e=1。
计算信息熵冗余度（差异）：
计算各项指标的权重：
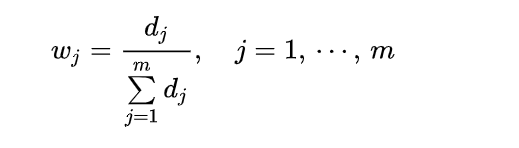
计算各样本的综合得分：

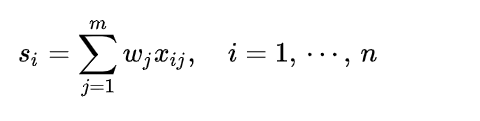
注意，这里的x_ij是归一化后的取值，即第一步的结果。

熵权悖论的解释

由此可知，权重与信息熵冗余度d正相关，与信息熵e是负相关的。也就是说，方差越大，熵越小，包含的信息越多，权重应当越大。
这里与前面的结论相悖的原因就在于熵权法计算熵的公式中，p不是各取值的比例，而是各个取值的相对大小。公式不一样，结论自然不一样了。

Python实现信息熵求权重

import pandas as pd
import numpy as np
import math


def nml(series):  # 正向指标归一化 减最小值的min-max方法
    l = []
    for i in series:
        l.append((i - series.min()) / (series.max() - series.min()))
    return pd.Series(l, name=series.name)

def nml_max(series): #负向指标归一化
    l = []
    for i in series:
        l.append((series.max() - i) / (series.max() - series.min()))
    return pd.Series(l, name=series.name)


def nmlzt(df): #归一化函数，对正负向指标分别调用nml()和nml_max()
    dfn = pd.DataFrame()
    for i in df.columns:
        if (i=='D'):
            dfn = pd.concat([dfn, nml_max(df[i])], axis=1)
        else:
            dfn = pd.concat([dfn, nml(df[i])], axis=1)
    # dfn为归一化的数据
    return dfn


def pij(df):  #求信息熵公式中的p，这里直接用取值除以取值总和，而不是数量的比例
    D = df.copy()
    for i in range(D.shape[1]):  # 列
        sum = D.iloc[:, i].sum()
        for j in range(D.shape[0]):  # 行
            D.iloc[j, i] = D.iloc[j, i] / sum
            # 算pij
    return D


def entropy(series):	#计算信息熵
    _len = len(series)

    def ln(x):
        if x > 0:
            return math.log(x)
        else:
            return 0

    s = 0
    for i in series:
        s += i * ln(i)
    return -(1 / ln(_len)) * s


def _result(dfij):	#求e、d、w并返回
    dfn = dfij.copy()
    w = pd.DataFrame(index=dfn.columns, dtype='float64')
    l = []
    for i in dfn.columns:
        l.append(entropy(dfn[i]))
    w['熵'] = l
    w['差异性系数'] = 1 - np.array(l)
    sum = w['差异性系数'].sum()
    l = []
    for i in w['差异性系数']:
        l.append(i / sum)
    w['权重'] = l
    return w

df = pd.read_csv('Blues_D.csv')	#读取你需要计算的文件
df=df[['D','GTI']]	#选取需要计算的属性列
dfn = nmlzt(df) #归一化
dfij = pij(dfn) #求p
w = _result(dfij)	#求权重
w.to_excel('weight_info_entropy.xlsx', sheet_name='权重')#输出结果
dfn = dfn.set_index(df.index, drop=True)
print(dfn)