D*（Dynamic A*）路径规划算法

0 概览

• 闲来无事，重新推导一下经典的 $D\ast$ 算法
• $D\ast$ 算法也就是 $Dynamic$ $A\ast$ 算法

1 $D\ast$

• $D\ast$ 算法是 $Dynamic$ $A\ast$ 的简称，是一种适应于动态环境的启发式的路径搜索算法
• 同 $A\ast$ 算法类似，$D\ast$ 通过一个维护一个优先队列 $OpenList$ 来对场景中的路径节点进行搜索。不同的是，$D\ast$ 从目标点开始搜索，通过将目标点置于 $OpenList$ 中来开始搜索，直到机器人当前位置节点从 $OpenList$ 出队为止
• $D\ast$ 分为两个阶段：第一阶段基于 $Dijkstra/A\ast$ 算法从目标点往起点进行搜索，得到搜索区域节点距离目标点最短路径的信息；第二阶段是动态避障搜索阶段（动态避障的时候，就可以充分利用在第一阶段当中所保存的信息，极大提高搜索效率）
• 因此 $D\ast$ 算法主要分为两个部分，第一部分是 $Process$ $State$，主要用于处理节点信息；第二部分是 $Modify$ $Cost$，主要用于修正若干个受障碍物影响而导致代价值发生变化的那些节点信息

1.1 $Process$ $State$

• 主要用于处理节点信息
• 第一阶段，环境障碍物已知，都是静态的

---

---

1.2 $Modify$ $Cost$

• 要用于修正若干个受障碍物影响而导致代价值发生变化的那些节点信息
• 第二阶段，动态避障，就需要充分利用第一阶段中所保存的信息

---

---

1.3 注意事项

• 算法将每一个节点的标识分为三类：

1. 还未被遍历到的节点为 $new$
2. 己经在 $OpenList$ 的为 $open$
3. 曾经在 $OpenList$ 但现在己经被移出的为 $closed$

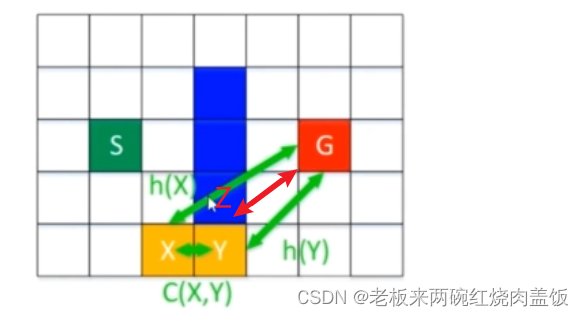
• 每个节点到目标点 $G$ 的代价为 $h$（这里参考了 $A\ast$ 算法的符号命名，并且 $D\ast$ 算法是从目标点到起始点方向进行搜索的；而在 $A\ast$ 算法里面，这是从起始点到目标点进行搜索的，$h$ 在 $A\ast$ 当中是代表当前节点到目标节点的一个估计代价；而 $h$ 在 $D\ast$ 当中是当前节点到目标节点的一个实际代价，如下图所示），两个节点 $X$ 与 $Y$ 之间的代价为 $C(X,Y)$

---

• $Tips$
• 一般横向竖向移动是 $1$
• 然后对角线代价一般是 $1.4$
• 这样就行
  

---

• $X$ 到终点的代价$h(X)$：为 $X$ 的父节点 $Y$ 到终点的代价 $h(Y)$ 加上 $X$ 和 $Y$ 之间的代价，即：$h(X)=h(Y)+C(X,Y)$
• 节点 $X$ 在不断遍历过程中，与目标点的代价会增大或减小（在不断遍历的过程当中，$h$ 会随着其父节点的变化而变化，如果 $Y$ 上面的那个点由障碍物变成了自由空间，假如这个点是 $Z$ 点，那么代价就该变为 $h(X)=h(Z)+C(X,Z)$，并且这个 $h(X)=h(Z)+C(X,Z)$ 是要小于 $h(X)=h(Y)+C(X,Y)$ 的，所以这个 $h$ 值就会减小，如下图所示）

---

• 假如这个点是 $Z$ 点，那么代价就该变为 $h(X)=h(Z)+C(X,Z)$，并且这个 $h(X)=h(Z)+C(X,Z)$ 是要小于 $h(X)=h(Y)+C(X,Y)$ 的，所以这个 $h$ 值就会减小
• 同理，假如当某一个点变成障碍物的时候，那么 $h$ 值可能就会增大
• 在增大或减小的这个过程当中，这个 $k$ 就是始终保持变化的 $h$ 的最小值，k = min(k, h);
  

---

• 设 $k$ 始终保持变化的 $h$ 的最小值。也就是说，对于标识为 $new$ 的点，表明还未遍历到，$k=h=inf(\infty )$

• 对于标识为 $open$ 或 $closed$ 的点， k = m i n { k , h n e w } k=min\{k,h_{new}\} k=min{k,hnew​}

• 这样就保证了 $open$ 或 $closed$ 的点代价最小

• 节点 $X$ 根据 $k$ 与 $h$ 的大小还有两种状态：若 $h=k$，记为 $Lower$ 态；若 $h>k$，记为 $Raise$ 态，表明有更优的路径（因为此时有 $k$ 更小的值，肯定有最优路径）

• 由于 $A\ast$ 和 $D\ast$ 的路径搜索方向相反，为避免混淆不同算法所定义的父节点、子节点概念，统一将离搜索起点更近的节点作为父节点

• 注意这里是搜索起点，$D\ast$ 与 $A\ast$ 反着来的，所以 $D\ast$ 的搜索起点是目标点，而 $A\ast$ 的搜索起点是 真正的那个起点

• 在 $A\ast$ 算法里面，是把离起点更近的点称为父节点，离目标点近的就是子节点

• 在 $D\ast$ 算法里面，因为搜索路径相反，所以离起点最近的点称为子节点，离目标点近的就是父节点

---

• $G$ 是搜索起点
• 比如这里 $Y$ 是 $X$ 的父节点，因为 $Y$ 离 $G$ 更近
• 然后 $X$ 就是 $Y$ 的子节点了
  

---

1.4 Code详解

1.4.1 $Process$ $State$ 详解

---

---

1.4.1.1 步骤1

步骤1. 在 $OpenList$ 中找到 $k$ 值最小的那个节点 $X$ 及对应的 $k_{old}$ 值，并从 $OpenList$ 当中移除

X = MIN_STATE();
if X = NULL then return -1;
k_old = GET_K_MIN();
DELETE(X);

• 记住，之前设了 $k$ 是始终保持变化的 $h$ 的最小值

1.4.1.2 步骤2

步骤2. 判断 $k_{old}$ 是否小于 $h(X)$，若确实小于的话，表明节点 $X$ 已经受到障碍的影响（之前说过了，假如当某一个点变成障碍物的时候，那么 $h$ 值可能就会增大），那么就遍历 $X$ 的邻节点看是否能够以某个邻节点作为父节点，使 $Nodes().h$ 变小（如果变小了，那么就变成了 $Lower$ 态，这个前面也说过，若 $h=k$，记为 $Lower$ 态；若 $h>k$，记为 $Raise$ 态，表明有更优的路径（因为此时有 $k$ 更小的值，肯定有最优路径））。执行上述步骤只表明 $h(X)$ 可以减小，但更新之后的 $h(X)$ 与 $k_{old}$ 相比，谁大谁小还尚未可知，需要继续判断，所以这一步是用来判断 $X$ 的父节点的

if k_old < h(X) then
	for each neighbor Y of X:
		if h(Y) <= k_old and h(X) > h(Y) + c(Y, X) then
		//上面这条语句就是说，h(X)也就是X直接到G的代价，是要比G到Y，再加上Y到X的代价要大的，如下图解释
			b(X) = Y;//找到代价更小的，就Y成为父节点
			h(X) = h(Y) + c(Y, X);//然后置换之前的代价

---

• 上面代码解释
  
• 就表示以 $Y$ 作为父节点这条路，由于直接从 $X$ 直接到 $G$ 这条路的
• 所以现在就可以更新， b(X) = Y;，就是 $Y$ 变成 $X$ 的父节点
• 再去更新 $h(X)$ 值

---

• 执行上述步骤只表明 $h(X)$ 可以减小，但是不一定能减小到刚好等于 $k_{old}$ ，且更新后的 $h(X)$ 与 $k_{old}$ 相比，谁大谁小还尚未可知，因为 $k_{old}$ 是之前存储的，所以需要继续判断，看下面的步骤3与步骤4，来综合判断

1.4.1.3 步骤3

• 步骤3的前提条件是 if k_old = h(X)，如果不能减小到 $k_{old}$，就看步骤4

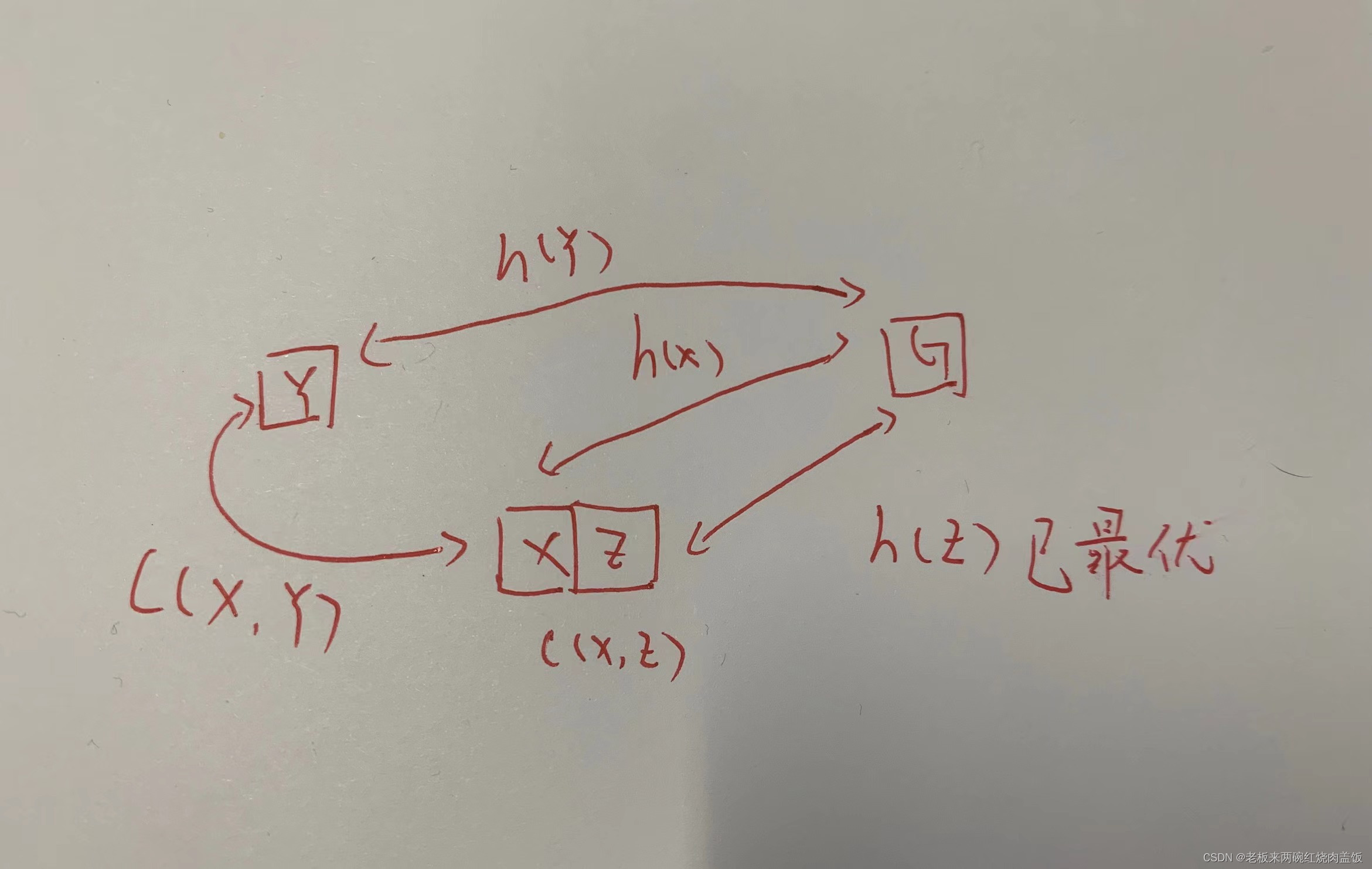
步骤3. 因为不知道更新后的 $k_{old}$ 与 $h(X)$ 谁大谁小，所以需要继续判断，若 $k_{old}=h(X)$，$Lower$ 态，此时 $X$ 无需判断，但需判断邻节点 $Y$ 是否有必要以 $X$ 作为父节点，也就是如下图

if k_old = h(X) then
	for each neighbor Y of X:
		if t(Y) = NEW or
			(b(Y) = X and h(Y) 不等于 h(X) + c(X, Y)) or
			(b(Y) = X;
			INSERT(Y, h(X) + c(X, Y))

---

• 如图，$h(Y)$ 这条路径已经是最优了，现在搜索 $X$ 的邻节点，是否能以 $X$ 作为其父节点
• 注意，图这里的与上述所说的 $Y$ 重了，注意不要混淆

• 具体看这
  

---

• 以下情况都参考上图
• 若情况1 t(Y) = NEW，表明邻节点 $Y$ 还未纳入 $OpenList$，那么就以 $X$ 作为父节点；
• 若情况2 b(Y) = X and h(Y) 不等于 h(X) + c(X, Y) ，表明虽然 $Y$ 的父节点是 $X$，但是 $h(Y)$ 却与 $h(X)+C(X,Y)$ 不相等了，表明 $Y$ 的父节点 $X$ 的 $h(X)$ 有过更新，可能是由于障碍引起的；
• 若情况3 b(Y) 不等于 X and h(Y) > h(X) + c(X, Y)，表明现在 $Y$ 的父节点不是 $X$，但是 $Y$ 可以通过将 $X$ 作为父节点，使得 $h(Y)$ 更小；
• 上述3种情况，都应该将 $X$ 作为 $Y$ 的父节点，并把 $Y$ 移到 $OpenList$ 后，再进一步考察

1.4.1.4 步骤4

• 前提条件 k_old 不等于 h(X)

步骤4. 若 $k_{old}$ 不等于 $h(X)$，则处于 $Raise$ 态，说明节点 $X$ 受到了影响，还未恢复为 $Lower$ 态，遍历其邻域 $Y$

for each neighbor Y of X:

步骤4.1.

• 若情况1，表明邻节点 $Y$ 还未纳入 $OpenList$；
• 若情况2，表明虽然 $Y$ 的父节点是 $X$，但是 $h(Y)$ 却不等于 $h(X)+c(X,Y)$。因此应该将 $X$ 作为 $Y$ 的父节点，更新 $Y$ 的 $h$ 值和 $k$ 值

for each neighbor Y of X:
	if t(Y) = NEW or
		(b(Y) = X and h(Y) 不等于 h(X) + c(X, Y)) then
			(b(Y) = X;
			INSERT(y, h(X) + c(X, Y))

步骤4.2.

• 步骤4.2.1. 若满足，表明 $Y$ 可以通过将 $X$ 作为父节点，使 $h(Y)$ 更小。但是 $X$ 自身还是 $Raise$ 态，故要先将 $X$ 追加到 $OpenList$，待下一次循环满足条件就将 $X$ 作为 $Y$ 的父节点
  • 可以看出，以下的代码与步骤3的差不多，但是为什么判断条件过后，执行语句不太一样呢？
  • 因为在步骤3当中，$X$ 是 $Lower$ 态，所以那时候可以直接把 $X$ 作为 $Y$ 的父节点插入进去
  • 但是现在步骤4当中，$X$ 还是 $Raise$ 态，所以需要先把 $X$ 追加到 $OpenList$ 当中，使得 $X$ 变为 $Lower$ 态，再循环一次，满足所有条件之后，就可以把 $X$ 作为 $Y$ 的父节点了，否则 $X$ 自己都没摆平，还去摆平子节点？

//接上面的if
else
	if b(Y) 不等于 X and h(Y) > h(X) + c(X, Y) then
		INSERT(X, h(X))

• 步骤4.2.2. 如果上方的4.2.1还没摆平，那么就执行4.2.2，$Y$ 的父节点不是$X$；让 $Y$ 成为 $X$ 父节点，$h(X)$ 更小；$Y$ 已经从 $OpenList$ 移除；当前从 $OpenList$ 取出的最小值 $k_{old}$ 居然比 $h(Y)$ 小（因为 $D\ast$ 应该是与 $Dijkstra$ 算法相类似的，正常的来说$k_{old}$ 应该是要比 $h(Y)$ 大的）。上述四个与条件，表明己经被 $OpenList$ 移出的 $Y$ 受到了障碍影响导致 $h$ 值升高，故要重新将 $Y$ 置于 $OpenList$ 中，进行下一轮考察

else
	if b(Y) 不等于 X and h(Y) > h(X) + c(X, Y) and
		t(Y) = CLOSED and h(Y) > k_old then 
		INSERT(Y, h(Y))

1.4.1.5 步骤5

• 返回 $k_{old}$ 及被修改的 $OpenList$ 信息

1.5 流程图

---

---

2 总结

以上就是 $D\ast$ 算法最核心的几个步骤，可以看出算法是相当复杂，怪不得后面出现了这么多改进的 $D\ast$ 算法