ADT: Stack 栈

ADT: Stack 栈

简介

本篇开始介绍 ADT(Abstract Data Type 抽象数据结构)，在计算机科学中除了基本类型如 int、long、char 等，大多数的程序还需要用到其他集成更多细节的抽象数据结构，如栈(Stack)、队列(Queue)、树(Tree)、图(Graph) 等，许多复杂算法的实现必须借助特定的数据结构才能够实现。

本篇将从最简单的栈(Stack)结构开始介绍，虽然栈的结构非常简单，但是透过简单的变形或是扩展能够运用在非常多的场景：

1. 单调栈：维护升(降)序排列的栈
2. 最小(大)栈：维护当前栈中最小(大)的元素
3. 中缀表达式转后缀表达式
4. 成对符号(括号、标签)匹配

接下来就来看看栈的概念和实现细节

参考

正文

栈结构

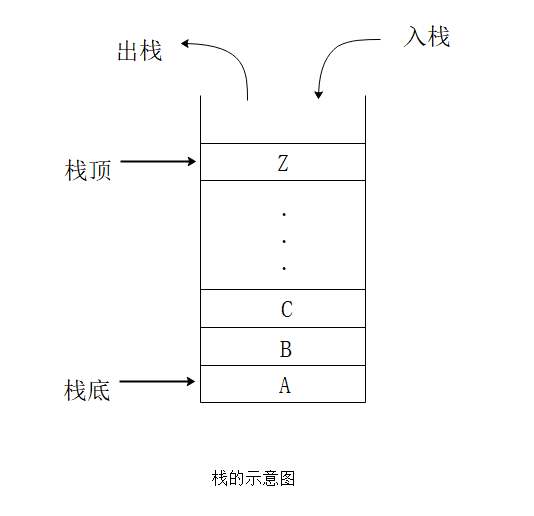图片来源：google图片

栈结构是一个只有单边开放的容器，入栈(添加元素)和出栈(取出元素)都是从同一边执行，属于后进先出(LIFO=Last-In-First-Out)的数据结构。

抽象接口

栈数据元素作为一个抽象的数据结构其实并不关心实现细节是使用数组还是链表，对于栈结构的操作统一透过约定好的公共接口来调用，以下是接口方法的说明

PUSH(x)
压(入)栈，将元素 x 加入到栈结构当中

POP()
出栈，将栈顶元素弹出并返回

TOP()
获取栈顶元素，但是不将其弹出栈结构

这边介绍的是最基本款的栈结构，如单调栈或是最大最小栈在实现细节上有额外的限制，这里就不多加说明。

实现要素

栈可以使用数组实现，也能够使用链表实现，这边介绍数组实现的细节。

使用数组来实现栈需要：

1. 维护一个保存元素的数组 T[] array
2. 记录当前数组的大小 int size
3. 记录当前栈顶位置 int top
4. 当数组被填满时扩展数组的方法 void expand()

Java 实现

首先提供 Java 的实现，使用了范型来增加数据结构的通用性：

• Stack.java

/**
 * 栈
 * @param <T>
 */
public interface Stack<T> {
    /**
     * 压栈
     * @param t
     */
    void push(T t);
    /**
     * 出栈
     * @return
     */
    T pop();
    /**
     * 获得栈顶元素
     * @return
     */
    T top();
}

• ``

public class StackWithArray<T> implements Stack<T> {
    public StackWithArray() {
        this(1); // 默认大小为 1
    }

    public StackWithArray(int size) {
        this.top = -1;
        this.size = size;
        this.array = (T[]) new Object[size];
    }

    private T[] array;
    private int size;
    private int top;

    /**
     * 压栈
     *
     * @param t
     */
    public void push(T t) {
        if (top == size - 1) extend();
        array[++top] = t;
    }

    /**
     * 出栈
     *
     * @return
     */
    public T pop() {
        if (top < 0) return null;
        return array[top--];
    }

    /**
     * 获得栈顶元素
     *
     * @return
     */
    public T top() { 
        return array[top]; 
    }

    /**
     * 扩展数组大小，每次扩展为当前大小的两倍
     */
    private void extend() {
        T[] newArray = (T[]) new Object[size * 2];
        for (int i = 0; i < size; i++) newArray[i] = array[i];
        array = newArray;
        size *= 2;
    }
}

• StackTest.java

public class StackTest {
    @Test
    public void test_stack_with_array() {
        Stack<Integer> stack = new StackWithArray<Integer>();
        Integer[] nums = new Integer[]{0, 4, 1, 5, 2, 6, 3, 0, 4, 7};
        for(int i=0 ; i<10 ; i++) stack.push(nums[i]);
        // 检查是否符合 LIFO 的顺序
        for(int i=9 ; i>=4 ; i--) {
            assertEquals(nums[i], stack.pop());
        }
        // 检查栈顶
        assertEquals((Integer)5, stack.top());
    }
}

C++ 实现

使用了 C++ 的模版类语法，所以声明定义都写在 header 文件内

• Stack.h

template<class T>
class Stack {
public:
    Stack();
    Stack(int);
    ~Stack();
    // 压栈
    void push(const T &);
    // 出栈
    T pop();

private:
    // 扩展数组
    void extend();

    T *_array; // 保存元素的数组
    int size; // 栈大小
    int top; // 栈顶指针
};

template<class T>
Stack<T>::Stack(): _array(new T[1]), size(1), top(-1) {}

template<class T>
Stack<T>::Stack(int size) :_array(new T[size]), size(size), top(-1) {}

template<class T>
Stack<T>::~Stack<T>() {
    delete[] _array;
}

template<class T>
void Stack<T>::push(const T &t) {
    if (top == size - 1) extend();
    _array[++top] = t;
}

template<class T>
T Stack<T>::pop() {
    if (top < 0) return nullptr;
    return _array[top--];
}

template<class T>
void Stack<T>::extend() {
    T *array = new T[size * 2];
    for (int i = 0; i < size; i++) {
        array[i] = _array[i];
    }
    _array = array;
    size *= 2;
}

template<class T>
void Stack<T>::info() {
    cout << "Stack: {size=" << size << ", nums: ";
    std::print(_array, size);
    cout << ", top=" << top << "}" << endl;
}

结语

栈结构非常的简单，但是又非常使用，大多数语言在内置库或第三方库(Java 中有 java.util.Stack 类)都提供性能优化后的栈结构，如果需要特别形式的栈或是对于初入栈有额外的定义则可以自己动手实现一个。