无约束最优化问题的求解算法

使用梯度下降法的目的和原因

目的

梯度下降法(Gradient Descent)是一个算法，但不是像多元线性回归那样是一个具体做回归任务的算法，而是一个非常通用的优化算法来帮助一些机器学习算法求解出最优解的，所谓的通用就是很多机器学习算法都是用它，甚至深度学习也是用它来求解最优解。所有优化算法的目的都是期望以最快的速度把模型参数θ求解出来，梯度下降法就是一种经典常用的优化算法。

原因

之前利用θ的解析解公式求解出来的解我们就直接说是最优解的一个原因是因为 MSE这个损失函数是凸函数，但是如果我们机器学习的损失函数是非凸函数的话，设置梯度为 0会得到很多个极值，甚至是极大值都有可能。
之前利用θ的解析解公式求解的另一个原因是特征维度并不多，但是细致分析一下公式里面 XT X 对称阵是 N 维乘以 N 维的，复杂度是是 O(N)的三次方，换句话说，就是如果你的特征数量翻倍，你的计算时间大致上要 2 的三次方，8 倍的慢比如，4 个特征 1 秒，8 个特征就是 8 秒，16 个特征就是 64 秒，当维度更多的时候呢？
所以其实之前一步求出最优解并不是机器学习甚至深度学习常用的手段，如下图，之前我们是设置梯度为 0，反过来求解最低点的时候θ是多少，而梯度下降法是一点点去逼近最优解！

梯度下降法的思想

其实这就跟生活中的情形很像，比如你问一个朋友的工资是多少，他说你猜？然后你会觉得很难猜，他说你猜完我告诉你是猜高了还是猜低了，这样你就可以奔着对的方向一直猜下去，最后总有一下你能猜对。梯度下降法就是这样的，你得去试很多次，而且是不是我们在试的过程中还得想办法知道是不是在猜对的路上，说白了就是得到正确的反馈再调整然后继续猜才有意义。
一般你玩儿这样的游戏的时候，一开始第一下都是随机瞎猜一个对吧，那对于计算机来说是不是就是随机取值，也就是说你有q =W1...Wn，这里θ强调一下不是一个值，而是一个向量就是一组 W，一开始的时候我们通过随机把每个值都给它随机出来。有了θ我们可以去根据算法就是公式去计算出来^y ，比如 y^ = Xq ，然后根据计算^y 和真实 y 之间的损失比如 MSE，然后调整θ再去计算 MSE。
这个调整正如咱们前面说的肯定不是瞎调整，当然这个调整的方式很多，你可以整体θ每个值调大一点，也可以整体θ每个值调小一点，也可以一部分调大一部分调小。第一次q 0我们可以得到第一次的 MSE 就是 Loss0，调整后第二次q1对应可以得到第二次的 MSE 就是 Loss1，如果 loss 变小是不是调对了，就应该继续调，如果 loss 反而变大是不是调反了，就应该反过来调。直到 MSE 我们找到最小值时计算出来的q^ 就是我们的最优解。
这个就好比道士下山，我们把 loss 看出是曲线就是山谷，如果走过来就再往回调，所以是一个迭代的过程。

梯度下降法公式

这里梯度下降法的公式就是一个式子指导计算机迭代过程中如何去调整θ，不需要推导和证明，就是总结出来的
Wjt+1 =Wjt -h ×gradientj 
这里的 Wj 就是θ中的某一个 j=0…n，这里的η就是图里的 learning step，很多时候也叫学习率 learning rate，很多时候也用α表示，这个学习率我们可以看作是下山迈的步子的大小，步子迈的大下山就快。

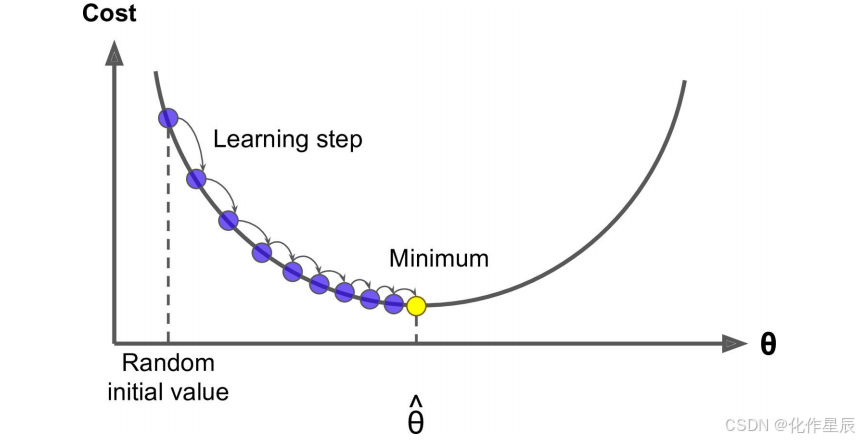
在梯度下降中，如果我们将损失函数可视化为一座山丘，那么：

• 当我们在“山”的左侧时（即梯度是负的），为了减少损失函数值，我们需要增加权重 W 的值。这是因为负梯度意味着我们处于一个下坡的位置，朝着梯度的反方向移动会让我们更接近山谷底部。
• 相反，在“山”的右侧（即梯度是正的），我们应该减小权重 W 的值，因为这同样是为了朝向损失函数的最小值前进。

每次权重 WjWj​ 调整的幅度就是 \[ W_j^{t+1} = W_j^t - \eta \cdot \text{gradient}_j \]，这是横轴上移动的距离，也即参数更新的步长。

如果特征或维度越多，那么这个公式用的次数就越多，也就是每次迭代要应用的这个式 子 n+1 次，所以其实上面的图不是特别准，因为θ对应的是很多维度，应该每一个维度都 可以画一个这的图，或者是一个多维空间的图。

\[ W_0^{t+1} = W_0^t - \eta \cdot g_0 \]

\[ W_1^{t+1} = W_1^t - \eta \cdot g_1 \]

\[ W_j^{t+1} = W_j^t - \eta \cdot g_j \]

\[ W_n^{t+1} = W_n^t - \eta \cdot g_n \]

其中：
- \( W_i^{t+1} \) 是参数 \( W_i \) 在下一次迭代（\( t+1 \)）的值。
- \( W_i^t \) 是参数 \( W_i \) 在当前迭代（\( t \)）的值。
- \( \eta \) 是学习率，控制每次更新的步长。
- \( g_i \) 是损失函数关于参数 \( W_i \) 的梯度。

这些公式展示了在多维空间中，每个参数 \( W_i \) 都会根据其对应的梯度 \( g_i \) 进行更新。

学习率设置

梯度下降公式

梯度下降的基本更新公式如下：

\[ W_j^{t+1} = W_j^t - \eta \cdot \text{gradient}_j \]

其中：
- \( W_j^{t+1} \) 是参数 \( W_j \) 在下一次迭代（\( t+1 \)）的值。
- \( W_j^t \) 是参数 \( W_j \) 在当前迭代（\( t \)）的值。
- \( \eta \) 是学习率，控制每次更新的步长。
- \( \text{gradient}_j \) 是损失函数关于参数 \( W_j \) 的梯度。

根据我们上面讲的梯度下降法公式，我们知道η是学习率，设置大的学习率 Wj 每次调整的幅度就大，设置小的学习率 Wj 每次调整的幅度就小，然而如果步子迈的太大也会有问题其实，俗话说步子大了容易扯着蛋，可能一下子迈到山另一头去了，然后一步又迈回来了，使得来来回回震荡。步子太小呢就一步步往前挪，也会使得整体迭代次数增加

学习率的设置是门学问，一般我们会把它设置成一个比较小的正整数，0.1、0.01、0.001、0.0001，都是常见的设定数值，一般情况下学习率在整体迭代过程中是一直不变的数，但是也可以设置成随着迭代次数增多学习率逐渐变小，因为越靠近山谷我们就可以步子迈小点，省得走过，还有一些深度学习的优化算法会自己控制调整学习率这个值

全局最优解

上图可以看出如果损失函数是非凸函数，梯度下降法是有可能落到局部最小值的，所以其实步长不能设置的太小太稳健，那样就很容易落入局部最优解，虽然局部最小值也没大问题，因为模型只要是堪用的就好了，但是我们肯定还是尽量要奔着全局最优解去。

梯度下降法流程

1，随机取，用random随 机θ，随机一组数值 W0…Wn

2. 求梯度，为什么是梯度？因为梯度代表曲线某点上的切线的斜率，沿着切线往下下 降就相当于沿着坡度最陡峭的方向下降

3. if g<0, theta 变大，if g>0, theta 变小

4. 判断是否收敛 convergence，如果收敛跳出迭代，如果没有达到收敛，回第 2 步继续

### 多维空间中的应用

在多维空间中，每个参数都有自己的梯度。假设我们有 \( n \) 个参数 \( W_1, W_2, \ldots, W_n \)，那么梯度也是一个向量，包含每个参数对应的梯度分量。

\[ \text{Gradient} = \left[ \text{gradient}_1, \text{gradient}_2, \ldots, \text{gradient}_n \right] \]

每次迭代中，所有参数都会根据各自的梯度进行同步更新：

\[ W_i^{t+1} = W_i^t - \eta \cdot \text{gradient}_i \quad \text{for } i = 1, 2, \ldots, n \]

### 示例

假设我们有两个参数 \( W_1 \) 和 \( W_2 \)，损失函数 \( L(W_1, W_2) \) 关于这两个参数的梯度分别是 \( \text{gradient}_1 \) 和 \( \text{gradient}_2 \)。那么更新公式可以写成：

\[ W_1^{t+1} = W_1^t - \eta \cdot \text{gradient}_1 \]
\[ W_2^{t+1} = W_2^t - \eta \cdot \text{gradient}_2 \]

### 总结

- **单变量情况**：对于单个参数的情况，梯度下降公式直观地展示了如何通过梯度信息调整参数以最小化损失。
- **多变量情况**：在多维空间中，每个参数都有自己的梯度，所有参数会在每次迭代中同步更新，逐步逼近损失函数的最小值。

希望这个解释能帮助你更好地理解梯度下降公式及其在多维空间中的应用。