MATLAB学习笔记(12 线性方程式和线性系统 Linear equations)
如想获得更好得阅读体验,可以转到后面链接 12
文章目录
1. 线性方程 (Linear Equation)
1.1 提出问题
题目:
对于一个电路网络:

给出电压 V 1 V_1 V1 和 V 2 V_2 V2 、电阻 R 1 . . . R 5 R_1...R_5 R1...R5,求解电流 i 1 . . . i 5 i_1...i_5 i1...i5.
解:
根据基尔霍夫电压电流定律(KCL/KVL),可得到:
[基尔霍夫定律内容](基尔霍夫定律(电学定律)_百度百科 (baidu.com))
V
1
=
R
1
i
1
+
R
4
i
4
R
4
i
4
=
R
2
i
2
+
R
5
i
5
R
5
i
5
=
R
3
i
3
+
V
2
i
1
=
i
2
+
i
4
i
2
=
i
3
+
i
5
\begin{aligned} & V_{1}=R_{1} i_{1}+R_{4} i_{4} \\ & R_{4} i_{4}=R_{2} i_{2}+R_{5} i_{5} \\ & R_{5} i_{5}=R_{3} i_{3}+V_{2} \\ & i_{1}=i_{2}+i_{4} \\ & i_{2}=i_{3}+i_{5} \end{aligned}
V1=R1i1+R4i4R4i4=R2i2+R5i5R5i5=R3i3+V2i1=i2+i4i2=i3+i5
转换为矩阵形式:
[
R
1
0
0
R
4
0
0
R
2
0
−
R
4
R
5
0
0
−
R
3
0
R
5
1
−
1
0
−
1
0
0
1
−
1
0
−
1
]
⏟
A
[
i
1
i
2
i
3
i
4
i
5
]
⏟
x
=
[
V
1
0
V
2
0
0
]
⏟
b
\underbrace{\left[\begin{array}{ccccc} R_{1} & 0 & 0 & R_{4} & 0 \\ 0 & R_{2} & 0 & -R_{4} & R_{5} \\ 0 & 0 & -R_{3} & 0 & R_{5} \\ 1 & -1 & 0 & -1 & 0 \\ 0 & 1 & -1 & 0 & -1 \end{array}\right]}_{\boldsymbol{A}} \underbrace{\left[\begin{array}{c} i_{1} \\ i_{2} \\ i_{3} \\ i_{4} \\ i_{5} \end{array}\right]}_{\boldsymbol{x}}=\underbrace{\left[\begin{array}{c} V_{1} \\ 0 \\ V_{2} \\ 0 \\ 0 \end{array}\right]}_{\boldsymbol{b}}
A
⎣
⎡R100100R20−1100−R30−1R4−R40−100R5R50−1⎦
⎤x
⎣
⎡i1i2i3i4i5⎦
⎤=b
⎣
⎡V10V200⎦
⎤
得到的矩阵方程中, A A A 和 b b b 已知, x x x 未知,需要求解 x x x.
1.2 求解线性方程组
可以使用的方法:
-
消元法 (Successive elimination (通过因式分解))
包括高斯消去法、LU分解
-
克莱默法则 (Cramer’s method)
1.3 高斯消去法 (Gaussian Elimination)
1.3.1 数学解释:
将增广矩阵进行 行与行之间的化简,尽可能使增广矩阵的左下方数字为 0
example:
给定方程组:
{
x
+
2
y
+
z
=
2
2
x
+
6
y
+
z
=
7
x
+
y
+
4
z
=
3
\left\{ \begin{array}{r} x+2y+z=2\\ 2x+6y+z=7\\ x+y+4z=3\\ \end{array} \right.
⎩
⎨
⎧x+2y+z=22x+6y+z=7x+y+4z=3
求解过程:
{
x
+
2
y
+
z
=
2
2
x
+
6
y
+
z
=
7
x
+
y
+
4
z
=
3
⟹
[
1
2
1
2
2
6
1
7
1
1
4
3
]
(写成增广矩阵的形式)
⇒
[
1
2
1
2
0
2
−
1
3
0
−
1
3
1
]
(行与行相减)
⇒
[
1
2
1
2
0
2
−
1
3
0
0
5
/
2
5
/
2
]
\begin{aligned} & \ \ \ \ \ \ \left\{ \begin{array}{r} x+2y+z=2\\ 2x+6y+z=7\\ x+y+4z=3\\ \end{array} \right. \Longrightarrow \left[ \begin{matrix} 1& 2& 1& 2\\ 2& 6& 1& 7\\ 1& 1& 4& 3\\ \end{matrix} \right] \text{(写成增广矩阵的形式)} \\ & \Rightarrow \left[ \begin{matrix} 1& 2& 1& 2\\ 0& 2& -1& 3\\ 0& -1& 3& 1\\ \end{matrix} \right] \text{(行与行相减)}\Rightarrow \left[ \begin{matrix} 1& 2& 1& 2\\ 0& 2& -1& 3\\ 0& 0& 5/2& 5/2\\ \end{matrix} \right] \end{aligned}
⎩
⎨
⎧x+2y+z=22x+6y+z=7x+y+4z=3⟹⎣
⎡121261114273⎦
⎤(写成增广矩阵的形式)⇒⎣
⎡10022−11−13231⎦
⎤(行与行相减)⇒⎣
⎡1002201−15/2235/2⎦
⎤
通过最后的矩阵列方程组求出解
x
=
[
x
1
,
x
2
,
x
3
]
x=[x_1,x_2,x_3]
x=[x1,x2,x3]
1.3.2 MTALAB 方法:rref()
A = [1 2 1;2 6 1;1 1 4];
b = [2; 7; 3];
R = rref([A b]) %使用 rref 以简化行阶梯形矩阵表示该方程组。
>> Class12
R =
1 0 0 -3
0 1 0 2
0 0 1 1
1.4 LU分解 (LU Factorization)
-
假设我们要求解: A x = b Ax=b Ax=b, 其中 A ∈ R m × m A\in R^{m\times m} A∈Rm×m
-
将 A A A 分解为2个三角矩阵: A = L − 1 U A=L^{-1}U A=L−1U
-
则问题转化为: A x = b ⟹ L − 1 U x ⏟ y = b Ax=b\Longrightarrow L^{-1}\underset{y}{\underbrace{Ux}}=b Ax=b⟹L−1y Ux=b
-
策略方法:
- 求解 L − 1 y = b L^{-1}y=b L−1y=b 得到 y y y
- 求解 U x = y Ux=y Ux=y
1.4.1 上/下三角矩阵定义
-
下三角矩阵 L = [ 1 0 0 ⋮ ⋱ 0 ⋮ ⋯ 1 ] ∈ R m × m \boldsymbol{L}=\left[ \begin{matrix} 1& 0& 0\\ \vdots& \ddots& 0\\ \vdots& \cdots& 1\\ \end{matrix} \right] \in \mathfrak{R} ^{m\times m} L=⎣ ⎡1⋮⋮0⋱⋯001⎦ ⎤∈Rm×m(对角线为1)
-
上三角矩阵 U = [ ⋮ ⋯ ⋮ 0 ⋱ ⋮ 0 0 ⋮ ] ∈ R m × m \boldsymbol{U}=\left[ \begin{matrix} \vdots& \cdots& \vdots\\ 0& \ddots& \vdots\\ 0& 0& \vdots\\ \end{matrix} \right] \in \mathfrak{R} ^{m\times m} U=⎣ ⎡⋮00⋯⋱0⋮⋮⋮⎦ ⎤∈Rm×m
1.4.2 如何获得 L L L 和 U U U ?
使用一系列的左乘:$
\underbrace{\boldsymbol{L}{m} \ldots \boldsymbol{L}{2} \boldsymbol{L}{1}}{\boldsymbol{L}} \boldsymbol{A}=\boldsymbol{U}$
1.4.2 LU 分解举例
对于一个矩阵: A = [ 1 1 1 2 3 5 4 6 8 ] \boldsymbol{A}=\left[\begin{array}{lll}1 & 1 & 1 \\ 2 & 3 & 5 \\ 4 & 6 & 8\end{array}\right] A=⎣ ⎡124136158⎦ ⎤
解:
先左乘一个矩阵
L
1
L_1
L1,其中
L
1
L_1
L1 是在单元矩阵
E
=
∣
1
0
0
0
1
0
0
0
1
∣
\boldsymbol{E}=\left| \begin{matrix} 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ \end{matrix} \right|
E=∣
∣100010001∣
∣ 的基础上补充得到,
L
1
A
L_{1}A
L1A 相乘使得矩阵
A
A
A 中的元素
x
21
=
2
x_{21}=2
x21=2 和
x
31
=
4
x_{31}=4
x31=4 化简为
0
0
0:
L
1
A
=
[
1
0
0
−
2
1
0
−
4
0
1
]
[
1
1
1
2
3
5
4
6
8
]
=
[
1
1
1
0
1
3
0
2
4
]
\boldsymbol{L}_{1} \boldsymbol{A}=\left[\begin{array}{ccc} 1 & 0 & 0 \\ -2 & 1 & 0 \\ -4 & 0 & 1 \end{array}\right]\left[\begin{array}{lll} 1 & 1 & 1 \\ 2 & 3 & 5 \\ 4 & 6 & 8 \end{array}\right]=\left[\begin{array}{lll} 1 & 1 & 1 \\ 0 & 1 & 3 \\ 0 & 2 & 4 \end{array}\right]
L1A=⎣
⎡1−2−4010001⎦
⎤⎣
⎡124136158⎦
⎤=⎣
⎡100112134⎦
⎤
同理,左乘一个矩阵
L
2
L_2
L2 ,
L
2
(
L
1
A
)
L_2(L_1A)
L2(L1A) 使得矩阵
L
1
A
L_1A
L1A 中的元素
x
32
=
2
x_{32}=2
x32=2 化简为
0
0
0。
L
2
(
L
1
A
)
=
[
1
0
0
0
1
0
0
−
2
1
]
[
1
1
1
0
1
3
0
2
4
]
=
[
1
1
1
0
1
3
0
0
−
2
]
=
U
\boldsymbol{L}_{2}\left(\boldsymbol{L}_{1} \boldsymbol{A}\right)=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -2 & 1 \end{array}\right]\left[\begin{array}{lll} 1 & 1 & 1 \\ 0 & 1 & 3 \\ 0 & 2 & 4 \end{array}\right]=\left[\begin{array}{rrr} 1 & 1 & 1 \\ 0 & 1 & 3 \\ 0 & 0 & -2 \end{array}\right]=\boldsymbol{U}
L2(L1A)=⎣
⎡10001−2001⎦
⎤⎣
⎡100112134⎦
⎤=⎣
⎡10011013−2⎦
⎤=U
由此求解出 L = L 2 L 1 L=L_2 L_1 L=L2L1 和 U U U.
1.4.3 MATLAB 方法: lu()
- matlab 中的
lu()函数在输入一个矩阵 A 之后,可以得到 L, U, P,其语法为[L,U,P]=lu(A),数学关系满足: P A = L U PA=LU PA=LU - 计算 A x = b A x=b Ax=b, 由 P A = L U P A=L U PA=LU 可得到: P − 1 L U x = b P^{-1} L U x=b P−1LUx=b, $\text { 令 } y=L^{-1} Pb \text {, 有 } U x=y $
example:
给出:
A
=
[
1
1
1
2
3
5
4
6
8
]
b
=
[
2
7
3
]
\boldsymbol{A}=\left[\begin{array}{lll} 1 & 1 & 1 \\ 2 & 3 & 5 \\ 4 & 6 & 8 \end{array}\right] \quad \boldsymbol{b}=\left[\begin{array}{l} 2 \\ 7 \\ 3 \end{array}\right]
A=⎣
⎡124136158⎦
⎤b=⎣
⎡273⎦
⎤
A = [1 1 1;2 3 5;4 6 8];
[L, U, P] = lu(A);
- 方法一:(matlab 中的数学计算方法)
得到 L , P , b L,P,b L,P,b 可利用 $ y=L^{-1} Pb$ 求 y y y,可利用 U x = y b U x=y b Ux=yb 关系式求解 x x x。
- 方法二:(老师的方法)
{ L − 1 y = b U x = y \left\{\begin{array}{c} L^{-1} y=b \\ U x=y \end{array}\right. {L−1y=bUx=y
1.4.4 矩阵的逆的快速表示:\
对于方程组:
{
x
+
2
y
+
z
=
2
2
x
+
6
y
+
z
=
7
x
+
y
+
4
z
=
3
\left\{\begin{array}{r} x+2 y+z=2 \\ 2 x+6 y+z=7 \\ x+y+4 z=3 \end{array}\right.
⎩
⎨
⎧x+2y+z=22x+6y+z=7x+y+4z=3
A = [1 2 1;2 6 1;1 1 4];
b = [2; 7; 3];
x = A\b
exercise (P14)(有疑惑)
题目:
Write a function to solve
i
1
…
i
5
for given
V
1
,
V
2
, and
R
1
…
R
5
\text { Write a function to solve } i_{1} \ldots i_{5} \text { for given } V_{1}, V_{2} \text {, and } R_{1} \ldots R_{5}
Write a function to solve i1…i5 for given V1,V2, and R1…R5
V
1
=
R
1
i
1
+
R
4
i
4
R
4
i
4
=
R
2
i
2
+
R
5
i
5
R
5
i
5
=
R
3
i
3
+
V
2
i
1
=
i
2
+
i
4
i
2
=
i
3
+
i
5
\begin{aligned} & V_{1}=R_{1} i_{1}+R_{4} i_{4} \\ & R_{4} i_{4}=R_{2} i_{2}+R_{5} i_{5} \\ & R_{5} i_{5}=R_{3} i_{3}+V_{2} \\ & i_{1}=i_{2}+i_{4} \\ & i_{2}=i_{3}+i_{5} \end{aligned}
V1=R1i1+R4i4R4i4=R2i2+R5i5R5i5=R3i3+V2i1=i2+i4i2=i3+i5
解:
% LU分解
clear
clc
syms R1 R2 R3 R4 R5 i1 i2 i3 i4 i5 V1 V2 V3 V4 V5
%根据方程组列出矩阵方程Ax=b,其中x与电流i有关
A=[R1 0 0 R4 0;...
0 R2 0 -R4 R5;...
0 0 -R3 0 R5;...
-1 1 0 1 0;...
0 -1 1 0 1];
x=[i1; i2; i3; i4; i5];
b=[V1; V2; V3; V4; V5];
[L,U,P]=lu(A);
% matlab的数学计算方法
x1 = x;
y1 = L\(P*b);
x1 = U\y1;
% 老师的方法
x2 = x;
y2 = L*b;
x2 = U\y2;
(解出来的 x1 和 x2 不一致,比较疑惑)
1.5 克莱默法则(Cramer’s (Inverse) Method)
内容:
- 问题如下:
[ 3 − 2 1 4 ] ⏟ A x y ] ⏟ x = [ 5 11 ] ⏟ b \underbrace{\left[\begin{array}{cc} 3 & -2 \\ 1 & 4 \end{array}\right]}_{A} \underbrace{\left.\begin{array}{l} x \\ y \end{array}\right]}_{x}=\underbrace{\left[\begin{array}{c} 5 \\ 11 \end{array}\right]}_{b} A [31−24]x xy]=b [511]
- 假设存在 A − 1 A^{-1} A−1 使得 A A − 1 = A − 1 A = E A A^{-1}=A^{-1} A=E AA−1=A−1A=E
- 则变量 x x x 为: x = A − 1 b x=A^{-1}b x=A−1b
1.5.1 逆矩阵(Inverse Matrix)
- 对于矩阵 A A A,其逆矩阵定义如下:
A − 1 = [ a b c d ] − 1 = 1 det ( A ) adj ( A ) = 1 det ( A ) [ d − b − c a ] \boldsymbol{A}^{-1}=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]^{-1}=\frac{1}{\operatorname{det}(\boldsymbol{A})} \operatorname{adj}(\boldsymbol{A})=\frac{1}{\operatorname{det}(\boldsymbol{A})}\left[\begin{array}{cc} d & -b \\ -c & a \end{array}\right] A−1=[acbd]−1=det(A)1adj(A)=det(A)1[d−c−ba]
其中 d e t ( A ) det(A) det(A) 表示 A A A 的行列式: det ( A ) = ∣ a d − b c ∣ \operatorname{det}(\boldsymbol{A})=|a d-b c| det(A)=∣ad−bc∣
- 性质: A = ( A − 1 ) − 1 , ( k A ) − 1 = k − 1 A − 1 \boldsymbol{A}=(\boldsymbol{A}^{-1})^{-1},(k \boldsymbol{A})^{-1}=k^{-1} \boldsymbol{A}^{-1} A=(A−1)−1,(kA)−1=k−1A−1
example:(使用克莱姆法则求解方程组)
题目:
{
x
+
2
y
+
z
=
2
2
x
+
6
y
+
z
=
7
x
+
y
+
4
z
=
3
⇒
[
1
2
1
2
6
1
1
1
4
]
x
=
[
2
7
3
]
\left\{\begin{array}{r} x+2 y+z=2 \\ 2 x+6 y+z=7 \\ x+y+4 z=3 \end{array} \Rightarrow\left[\begin{array}{lll} 1 & 2 & 1 \\ 2 & 6 & 1 \\ 1 & 1 & 4 \end{array}\right] x=\left[\begin{array}{l} 2 \\ 7 \\ 3 \end{array}\right]\right.
⎩
⎨
⎧x+2y+z=22x+6y+z=7x+y+4z=3⇒⎣
⎡121261114⎦
⎤x=⎣
⎡273⎦
⎤
解:
x = A − 1 b x=A^{-1}b x=A−1b
A = [1 2 1;2 6 1;1 1 4];
b = [2; 7; 3];
x = inv(A)*b
exercise (P19)
题目:
- 在三维空间画该平面 { x + y + z = 0 x − y + z = 0 x + 3 z = 0 \left\{\begin{array}{c}x+y+z=0 \\ x-y+z=0 \\ x+3 z=0\end{array}\right. ⎩ ⎨ ⎧x+y+z=0x−y+z=0x+3z=0
解:
clear
clc
clf
x = 0:40;
y = 0:40;
[X1,Y1]=meshgrid(x,y); %画三维图之前绘制网格,可以参考高阶绘图部分讲义
[X2,Y2]=meshgrid(x,y);
[X3,Y3]=meshgrid(x,y);
Z1 = -X1-Y1;
Z2 = -X2+Y2;
Z3 = -1/3*X3;
hold on
surf(Y1,X1,Z1);
surf(Y2,X2,Z2);
surf(Y3,X3,Z3);
axis square;
hold off
%如果需要改变Y轴的方向和z轴的取值范围,可以在 Figure-查看-属性检查器 中更改
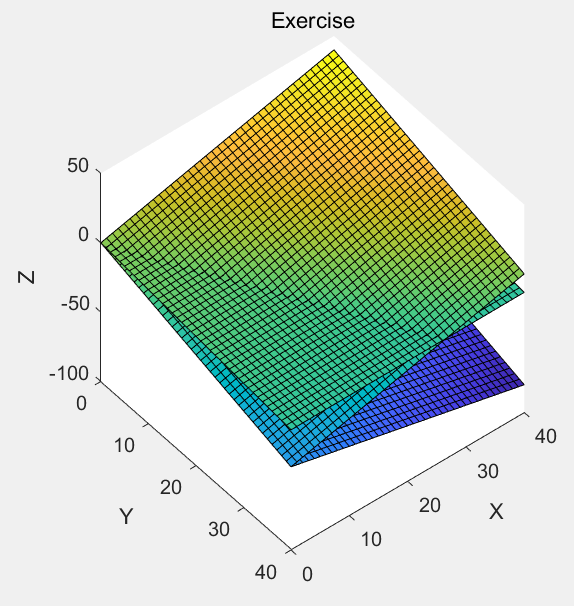
1.6 检查矩阵状况的函数:cond()
如果矩阵 A A A 出现下图中第二和第三种情况,则 A A A 的行列式为零( d e t ( A ) = 0 det(A)=0 det(A)=0,Singular):
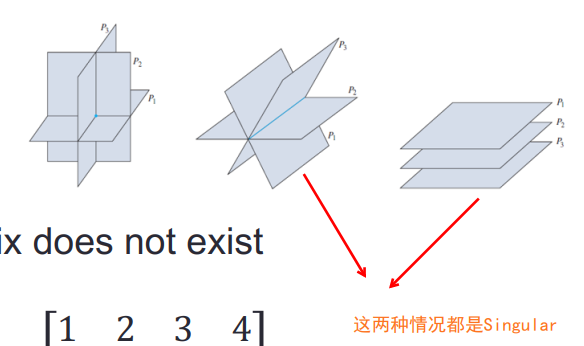
在 MATLAB 中可以使用 cond() 函数观察矩阵的“健康状况”,得到的值越小,矩阵对求逆运算越不敏感。
2. 线性系统 (Linear System)
2.1 提出问题
线性方程式是 A x = b Ax=b Ax=b 的形式,线性系统是 A b = y Ab=y Ab=y 的形式
-
给出方程组: { 2 ⋅ 2 − 12 ⋅ 4 = x 1 ⋅ 2 − 5 ⋅ 4 = y \left\{\begin{array}{l}2 \cdot 2-12 \cdot 4=x \\ 1 \cdot 2-5 \cdot 4=y\end{array}\right. {2⋅2−12⋅4=x1⋅2−5⋅4=y
-
矩阵表达形式:

2.2 特征值和特征向量 (Eigenvalues and Eigenvectors)
2.2.1 数学方法:
-
对于一个系统 A ∈ R m × m A\in R^{m\times m} A∈Rm×m,如果矩阵相乘 y = A b y=Ab y=Ab 比较复杂,可以找到一个向量 v v v,使得 A v i = λ i v i \boldsymbol{A} \boldsymbol{v}_{i}=\lambda_{i} \boldsymbol{v}_{i} Avi=λivi ,并且 λ i \lambda_{i} λi 为常数(把 v i v_i vi 称为特征向量, λ i \lambda_i λi 称为特征值)
-
然后分解 b = ∑ α i v i , α i ∈ ℜ \boldsymbol{b}=\sum \alpha_{i} \boldsymbol{v}_{i}, \alpha_{i} \in \Re b=∑αivi,αi∈ℜ
-
矩阵相乘变为:
A b = ∑ α i A v i = ∑ α i λ i v i \boldsymbol{A} \boldsymbol{b}=\sum \alpha_{i} \boldsymbol{A} \boldsymbol{v}_{i}=\sum \alpha_{i} \lambda_{i} \boldsymbol{v}_{i} Ab=∑αiAvi=∑αiλivi
2.2.2 特征值和特征向量的解释
对于矩阵
A
A
A 的特征值和特征向量:
{
A
v
1
=
λ
1
v
1
A
v
2
=
λ
2
v
2
\left\{\begin{array}{l} A v_{1}=\lambda_{1} v_{1} \\ A v_{2}=\lambda_{2} v_{2} \end{array}\right.
{Av1=λ1v1Av2=λ2v2
当输入为
v
1
v_{1}
v1 时, 如果
λ
1
>
1
\lambda_{1}>1
λ1>1, 称系统对输入进行放大;如果输入不是
v
1
v_{1}
v1, 可以对输入进行分解, 输入
=
(
α
1
v
1
+
α
2
v
2
)
=\left(\alpha_{1} v_{1}+\alpha_{2} v_{2}\right)
=(α1v1+α2v2)
example:
-
给出 A b = [ 2 − 12 1 − 5 ] [ 2 4 ] \boldsymbol{A} \boldsymbol{b}=\left[\begin{array}{cc}2 & -12 \\ 1 & -5\end{array}\right]\left[\begin{array}{l}2 \\ 4\end{array}\right] Ab=[21−12−5][24] (假如不想计算矩阵乘法,用求特征值的方法)
-
利用 MATLAB 的
eig()函数可以得到下面结果:(2.2.3部分有解释)
λ 1 v 1 = [ 0.97 0.24 ] , λ 2 v 2 = − 2 [ 0.95 0.32 ] \lambda_{1}\boldsymbol{v}_{1}=\left[\begin{array}{l} 0.97 \\ 0.24 \end{array}\right], \quad \lambda_{2} \boldsymbol{v}_{2}=-2\left[\begin{array}{l} 0.95 \\ 0.32 \end{array}\right] λ1v1=[0.970.24],λ2v2=−2[0.950.32]
-
把 b b b 拆解 b = α 1 v 1 + α 2 v 2 = − 41.2 v 1 + 44.3 v 2 \boldsymbol{b}=\alpha_{1} \boldsymbol{v}_{1}+\alpha_{2} \boldsymbol{v}_{2}=-41.2 \boldsymbol{v}_{1}+44.3 \boldsymbol{v}_{2} b=α1v1+α2v2=−41.2v1+44.3v2
-
计算 A b Ab Ab
A b = A ( α 1 v 1 + α 2 v 2 ) = α 1 A v 1 + α 2 A ( α 1 = v 1 + α 2 v 1 v 1 + α 2 λ 2 v 2 = ( − 41.2 ) ( − 1 ) [ 0.97 0.24 ] + ( 44.3 ) ( − 2 ) [ 0.95 0.32 ] \boldsymbol{Ab}=\boldsymbol{A}\left( \alpha _1\boldsymbol{v}_1+\alpha _2\boldsymbol{v}_2 \right) \\ =\alpha _1\boldsymbol{Av}_1+\alpha _2\boldsymbol{A}\left( \alpha _1=\boldsymbol{v}_1+\alpha _2\boldsymbol{v}_1\boldsymbol{v}_1+\alpha _2\lambda _2\boldsymbol{v}_2 \right. \\ =(-41.2)(-1)\left[ \begin{array}{l} 0.97\\ 0.24\\ \end{array} \right] +(44.3)(-2)\left[ \begin{array}{l} 0.95\\ 0.32\\ \end{array} \right] Ab=A(α1v1+α2v2)=α1Av1+α2A(α1=v1+α2v1v1+α2λ2v2=(−41.2)(−1)[0.970.24]+(44.3)(−2)[0.950.32]
2.2.3 算特征值和特征向量用 eig() 函数
求特征值和特征向量:
A
=
[
2
−
12
1
−
5
]
A=\left[ \begin{matrix} 2& -12\\ 1& -5\\ \end{matrix} \right]
A=[21−12−5]
[v,d] = eig([2 -12;1 -5])
2.3 矩阵指数:expm()
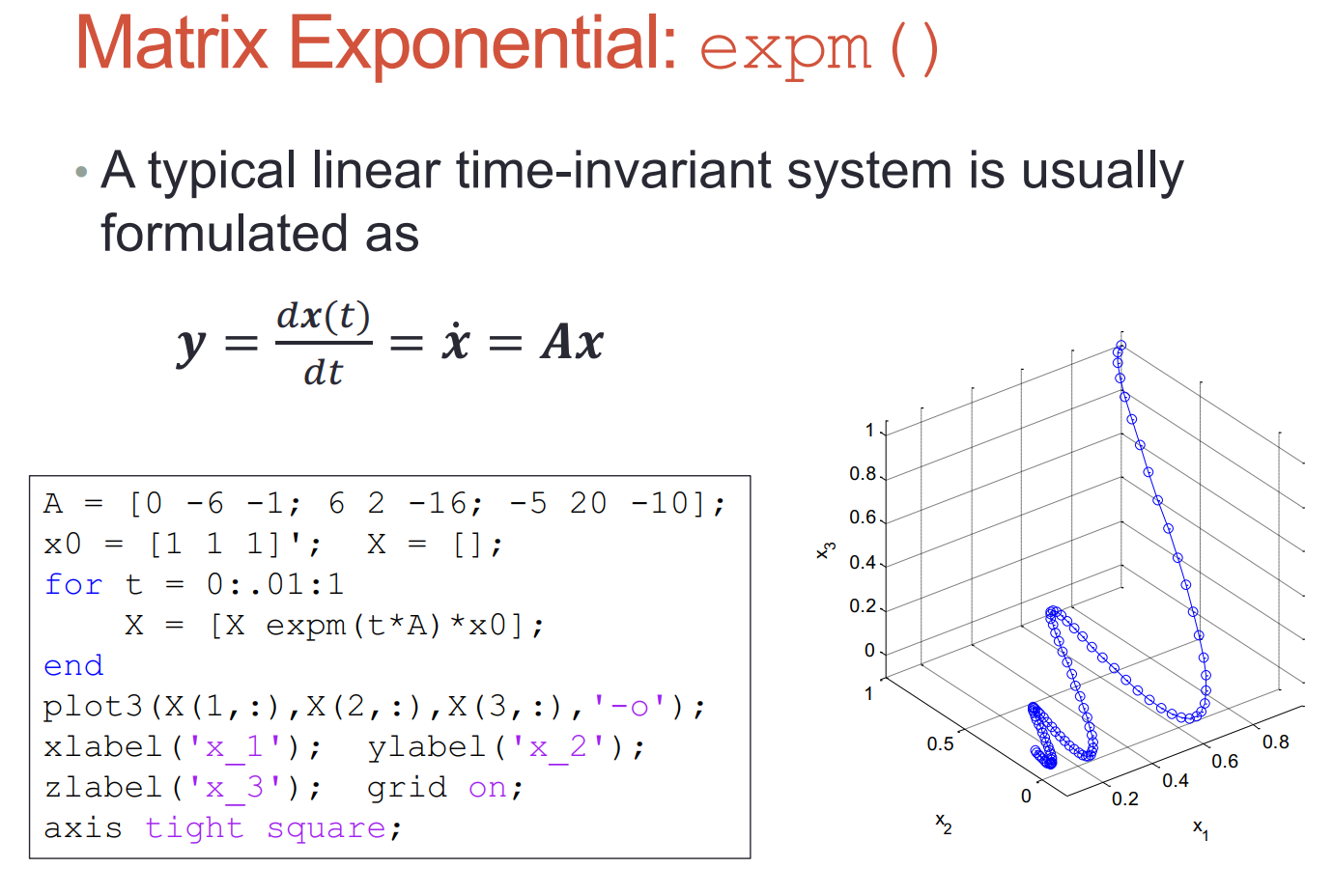




















 101
101











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








