模拟集成电路笔记 | 第二部分 | Chapter 4
如想获得更好的阅读体验,可参考 02-CMOS模拟集成电路
第四章 差动放大器
4.1 单端和差动的工作方式
差动工作相比单端工作的优势:
-
对环境噪声具有更强的抗干扰能力
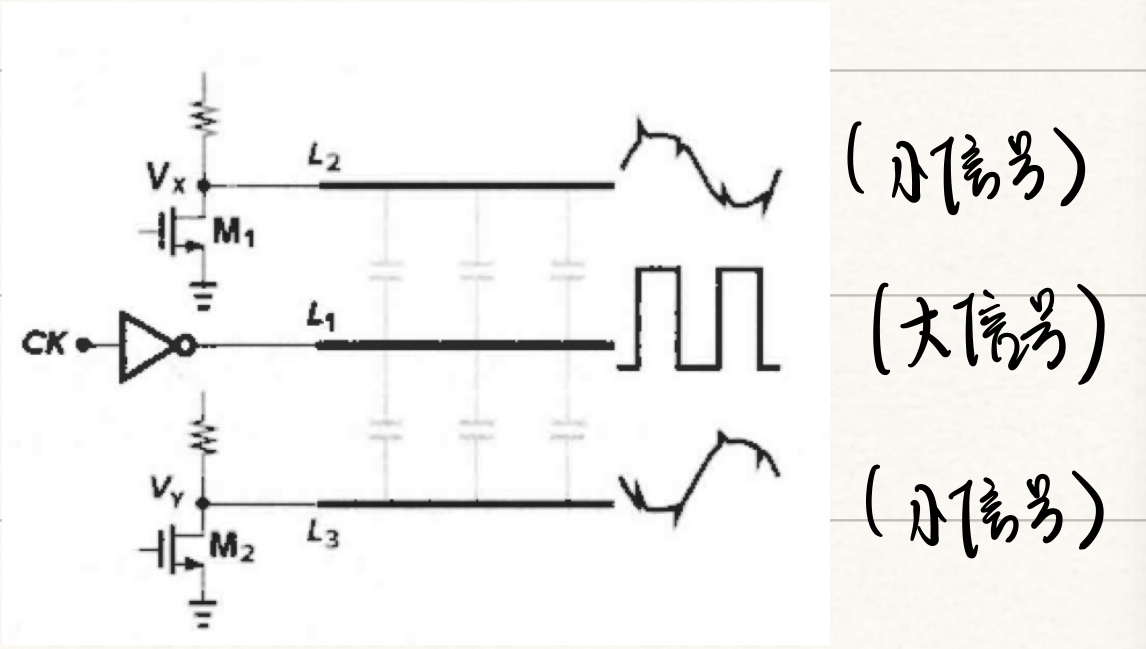
小信号取差值可以消除大信号(时钟跃变)带来的干扰
-
更大的输出摆幅
4.2 基本差动对
4.2.1 定性分析
-
基本差动对
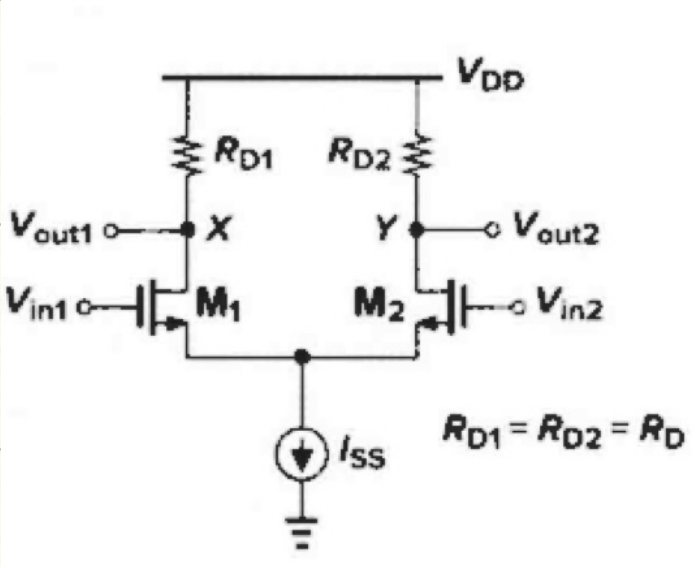
-
差动分析
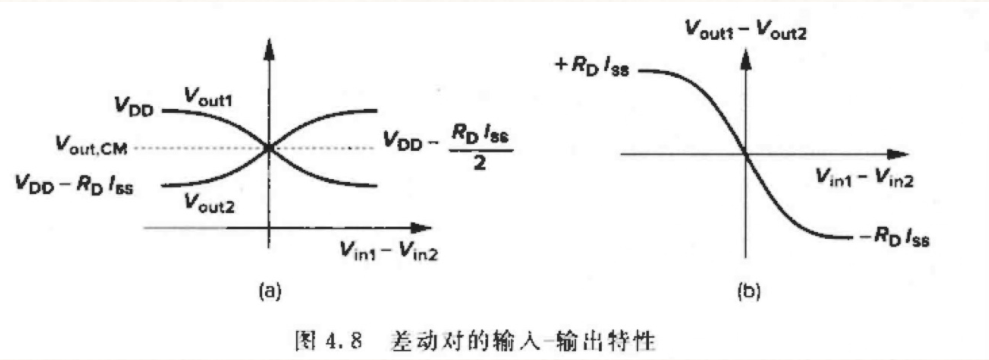
分析:
V i n 1 − V i n 2 V_{in1}-V_{in2} Vin1−Vin2 从$-\infty $ 到 $+\infty $ 变化,当 Vin1 非常小时,M1 截止,M2 导通, I D 1 = 0 , l D 2 = I S S , V o u t 1 = V D D , V o u t 2 = V D D − R D × I s s I_{D1}=0,l_{D2} = I_{SS},V_{out1} = V_{DD},V_{out2} = V_{DD}- R_D~ \times I_{ss} ID1=0,lD2=ISS,Vout1=VDD,Vout2=VDD−RD ×Iss。同理当 Vin2 也非常小时有类似结果。特别地,当电路处于平衡状态( V i n 1 = V i n 2 V_{in1} = V_{in2} Vin1=Vin2) , I D 1 = I D 2 = I s s / 2 I_{D1}= I_{D2}= I_{ss}/2 ID1=ID2=Iss/2, V o u t 1 = V o u t 2 = V D D − I S S / 2 V_{out1} = V_{out2} = V_{DD} - I_{SS}/2 Vout1=Vout2=VDD−ISS/2。
重要特性:
- 输出最大/最小电平与输入共模电平无关。
- 相比简单差动电路,随着输出摆幅的增大,电路变得更加非线性(图4.8(b))
-
共模特性
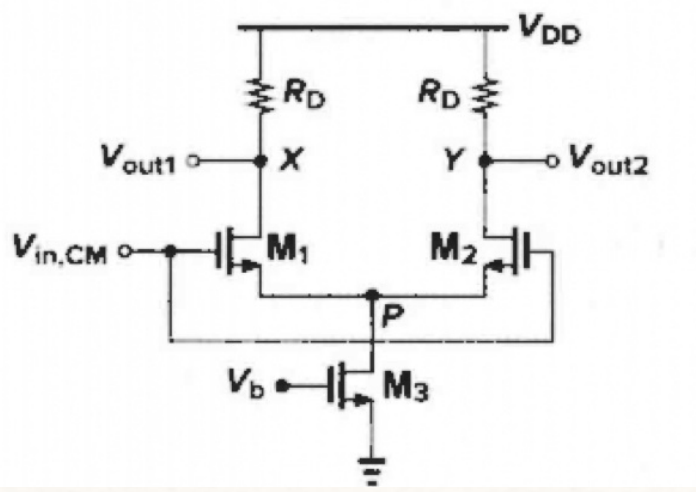
输入共模电平 Vin,CM 从 0 变化到 VDD
- 当 V i n , C M = 0 V_{in,CM}= 0 Vin,CM=0 时,M1,M2 截止,M3 在深线性区(因为 l D 3 = l D 2 = I D 1 = 0 l_{D3} = l_{D2} = I_{D1} =0 lD3=lD2=ID1=0,且 V b > V t h V_{b} > V_{th} Vb>Vth,得到 V p = 0 V_p= 0 Vp=0);
- 当 Vin 增大时,可以将 M3 当成一个电阻(因为在 VGS 不变的条件下,观察 lD 和 VDS 的关系可以知道,电流从 0 开始增大会先经过线性区),M1,M2 导通进入饱和区,ID1,ID2,lD3 也增大,Vp 也增大,
Vp大到一定程度使得 M3 进入饱和区; - Vin 进一步增大会使得 M1,M2 进入线性区。
为使电路正常工作,输入共模电平范围为:
V C S 1 + ( V G S 3 − V T H 3 ) ⏟ M 1 , M 2 导通, M 3 为饱和区和线性区边界 ⟹ V P > V G S 3 − V T H 3 ⩽ V i n , C M ⩽ min [ V D D − R D I S S 2 + V T H , V D O ] ⏟ 使 M 1 , M 2 为饱和区和线性区边界 ⟹ V G S 1 − V T H < V o u t = V D D − 1 2 I S S R D \underset{\begin{array}{c} M_1,M_2\text{导通,}M_3\text{为饱和区和线性区边界}\\ \Longrightarrow V_P>V_{GS3}-V_{TH3}\\ \end{array}}{\underbrace{V_{\mathrm{CS}1}+\left( V_{G\mathrm{S}3}-V_{\mathrm{TH}3} \right) }}\leqslant V_{\mathrm{in},\mathrm{CM}}\leqslant \underset{\begin{array}{c} \text{使}M_1,M_2\text{为饱和区和线性区边界}\\ \Longrightarrow V_{GS1}-V_{TH}<V_{out}=V_{DD}-\frac{1}{2}I_{SS}R_D\\ \end{array}}{\underbrace{\min \left[ V_{\mathrm{DD}}-R_{\mathrm{D}}\frac{I_{\mathrm{SS}}}{2}+V_{\mathrm{TH}}, V_{\mathrm{DO}} \right] }} M1,M2导通,M3为饱和区和线性区边界⟹VP>VGS3−VTH3 VCS1+(VGS3−VTH3)⩽Vin,CM⩽使M1,M2为饱和区和线性区边界⟹VGS1−VTH<Vout=VDD−21ISSRD min[VDD−RD2ISS+VTH,VDO]
4.2.2 定量分析
-
定量分析
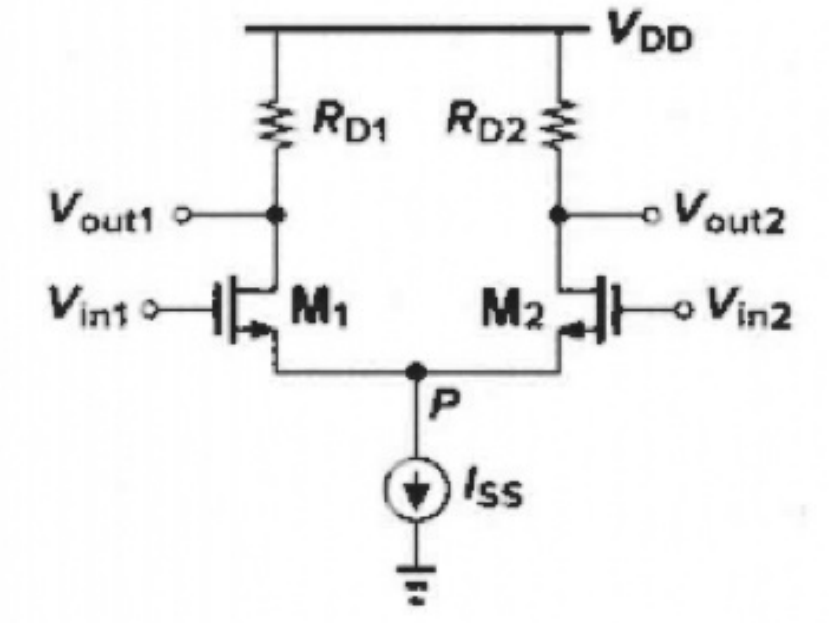
对差动对电路进行分析,确定 V o u t 1 − V o u t 2 V_{out1}- V_{out2} Vout1−Vout2与 V i n 1 − V i n 2 V_{in1}- V_{in2} Vin1−Vin2的函数关系:
V o u t 1 − V o u t 2 = R D ( I D 2 − I D 1 ) = R D Δ I = R D G m Δ V i n , ( 小信号) G m = ∂ Δ I D ∂ Δ V i n = 1 2 μ n C o x W L 4 I S S μ n C o x W / L − 2 Δ V i n 2 4 I s s μ n C o x W / L − Δ V i n 2 V_{\mathrm{ou}t1}-V_{\mathrm{out}2}=R_{\mathrm{D}}\left( I_{\mathrm{D}2}-I_{D1} \right) =R_{\mathrm{D}}\Delta I=R_{\mathrm{D}}G_{\mathrm{m}}\Delta V_{\mathrm{in}},\quad (\text{小信号)} \\ G_m=\frac{\partial \Delta I_{\mathrm{D}}}{\partial \Delta V_{\mathrm{in}}}=\frac{1}{2}\mu _{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}\frac{\frac{4I_{SS}}{\mu _{\mathrm{n}}C_{\mathrm{ox}}W/L}-2\Delta V_{\mathrm{in}}^{2}}{\sqrt{\frac{4I_{\mathrm{ss}}}{\mu _{\mathrm{n}}C_{\mathrm{ox}}W/L}-\Delta V_{\mathrm{in}}^{2}}} Vout1−Vout2=RD(ID2−ID1)=RDΔI=RDGmΔVin,(小信号)Gm=∂ΔVin∂ΔID=21μnCoxLWμnCoxW/L4Iss−ΔVin2μnCoxW/L4ISS−2ΔVin2
有漏极电流 I D 1 I D 2 \frac{I_{D1}}{I_{D2}} ID2ID1 和总跨导 Gm 随输入电压变化曲线: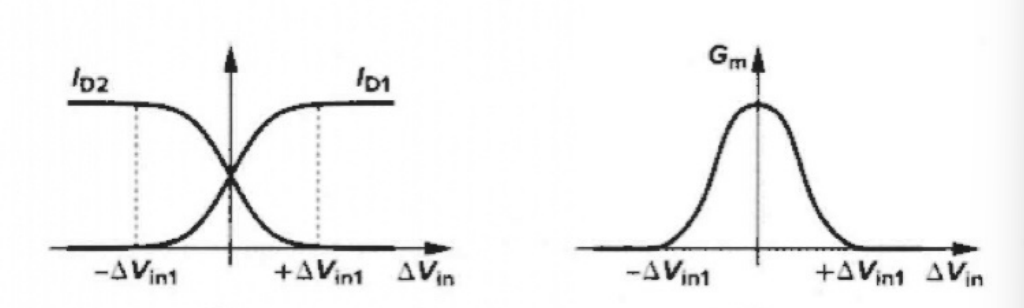
Δ V i n 1 \varDelta V_{in1} ΔVin1 为所有的 lss 流经一个晶体管,而另一个晶体管截止的情况。
Δ V i n l = 2 I S S μ n C o x ( W / L ) \Delta V_{\mathrm{inl}}=\sqrt{\frac{2 I_{\mathrm{SS}}}{\mu_{n} C_{o \mathrm{x}}(W / L)}} ΔVinl=μnCox(W/L)2ISS -
小信号分析
-
叠加法分析
(分别考虑只有一个输入时对输出 Vout1 和 Vout2 的影响, 再将两种结果相加) -
半边电路法(计算差模增益)
(找到交流地的点, 计算 V x / V i n 1 {V_x} / {V_{in1}} Vx/Vin1 和 V Y / − V i n 1 {V_Y} / {-V_{in1}} VY/−Vin1,再计算差模增益)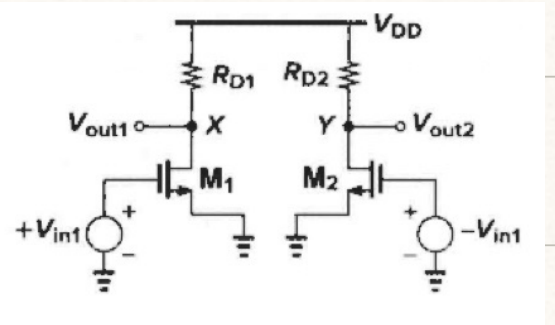
-
4.2.3 带源极负反馈的差动对

采用电阻负反馈可以提高线性度(简单分析 M1 导通,M2 截止的情况可得到,新电路使一边晶体管关断所需的差动电压的幅度增加,
Δ
V
i
n
1
变为
Δ
V
i
n
2
\Delta V_{in1} \ \ 变为 \ \ \Delta V_{in2}
ΔVin1 变为 ΔVin2)
Δ
V
i
n
2
−
Δ
V
i
n
1
=
R
S
I
S
S
\Delta V_{\mathrm{in} 2}-\Delta V_{\mathrm{in} 1}=R_{\mathrm{S}} I_{\mathrm{SS}}
ΔVin2−ΔVin1=RSISS
4.3 共模响应
(差动对对共模扰动影响具有抑制能力,但是共模输入的变化会或多或少地传递到输出端)
-
电流源具有有限的输出阻抗 RSS
共模输入的情况下 I D 1 = I D 2 , V o u t 1 = V o u t 2 I_{D1}= I_{D2},V_{out1}= V_{out2} ID1=ID2,Vout1=Vout2,电路可以等效为下图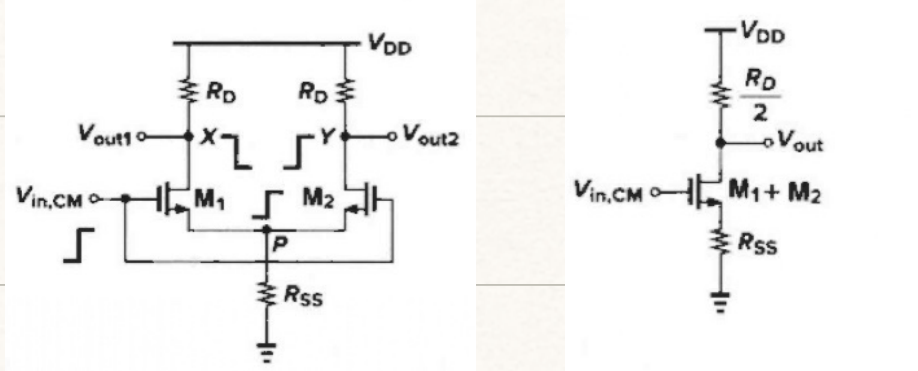
A V , C M = − R D / 2 1 / ( 2 g m ) + R s s A_{V,CM}=-\frac{R_{\mathrm{D}}/2}{1/\left( 2g_{\mathrm{m}} \right) +R_{\mathrm{ss}}} AV,CM=−1/(2gm)+RssRD/2
A V A_V AV 表示共模输入的变化会传递到输出 -
RD 电阻不对称且尾电流源的输出阻抗有限
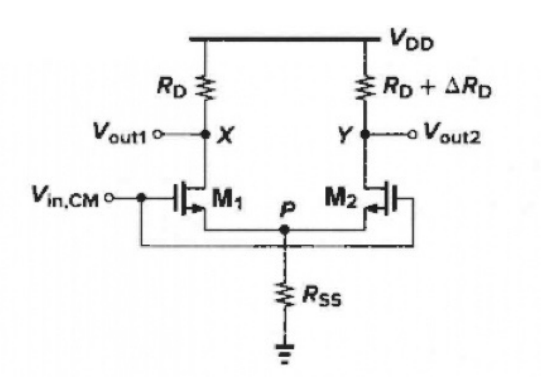
Δ V X = − Δ V i n , C M g m 1 + 2 g m R S S R D Δ V Y = − Δ V i n , C M g m 1 + 2 g m R S S ( R D + Δ R D ) \Delta V_X=-\Delta V_{\mathrm{in},CM}\frac{g_{\mathrm{m}}}{1+2g_{\mathrm{m}}R_{SS}}R_D \\ \Delta V_{\mathrm{Y}}=-\Delta V_{\mathrm{in},CM}\frac{g_{\mathrm{m}}}{1+2g_{\mathrm{m}}R_{\mathrm{SS}}}\left( R_{\mathrm{D}}+\Delta R_{\mathrm{D}} \right) ΔVX=−ΔVin,CM1+2gmRSSgmRDΔVY=−ΔVin,CM1+2gmRSSgm(RD+ΔRD)
分析:V X 、 V Y V_X、V_Y VX、VY不相等,输入端共模的变化 Δ V i n , C M \Delta V_{in,CM} ΔVin,CM 在输出端产生了一个差动成分 Δ R D \Delta R_D ΔRD,电路表现为共模到差模的转换
-
M1 管和 M2 管不匹配
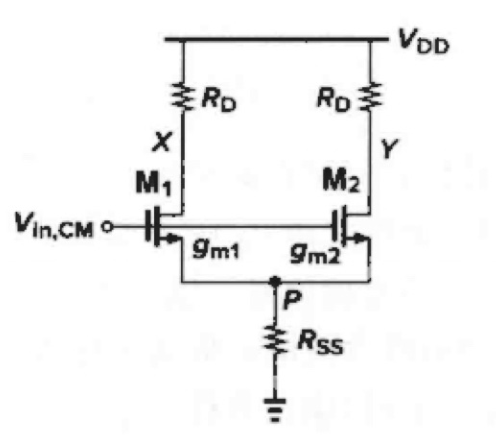
V x − V Y = − g m 1 − g m 2 ( g m 1 + g m 2 ) R ˙ S S + 1 R D V i n . C M A C M − D M = − Δ g m R D ( g m 1 + g m 2 ) R S s + 1 V_{\mathrm{x}}-V_Y=-\frac{g_{\mathrm{m}1}-g_{m2}}{\left( g_{m1}+g_{m2} \right) \dot{R}_{SS}+1}R_DV_{\mathrm{in}.CM} \\ A_{CM-\mathrm{DM}}=-\frac{\Delta g_{\mathrm{m}}R_D}{\left( g_{\mathrm{m}1}+g_{\mathrm{m}2} \right) R_{Ss}+1} \\ Vx−VY=−(gm1+gm2)R˙SS+1gm1−gm2RDVin.CMACM−DM=−(gm1+gm2)RSs+1ΔgmRD
其中 A C M − D M A_{\mathrm{CM}-\mathrm{DM}} ACM−DM 表示共模到差模的转换,且 Δ g m = g m 1 − g m 2 \Delta g_{\mathrm{m}}=g_{\mathrm{m}1}-g_{\mathrm{m}2} Δgm=gm1−gm2 -
共模抑制比 CMRR
C M R R = ∣ A D M A C M − D M ∣ (期望增益与非期望增益之比) CMRR=\left| \frac{A_{DM}}{A_{CM-DM}} \right|\text{(期望增益与非期望增益之比)} CMRR=∣ ∣ACM−DMADM∣ ∣(期望增益与非期望增益之比)
4.4 MOS为负载的差动对
(略)
4.5 吉尔伯特单元
(增益随控制电压变化而变化的差动对)
-
简单的可变增益放大器(VGA)

增益 A V = − g m R D A_V= -g_mR_D AV=−gmRD 是尾电流源的函数,控制电压 V c o n t V_{cont} Vcont 确定了尾电流的大小,从而决定了增益的大小
-
吉尔伯特单元
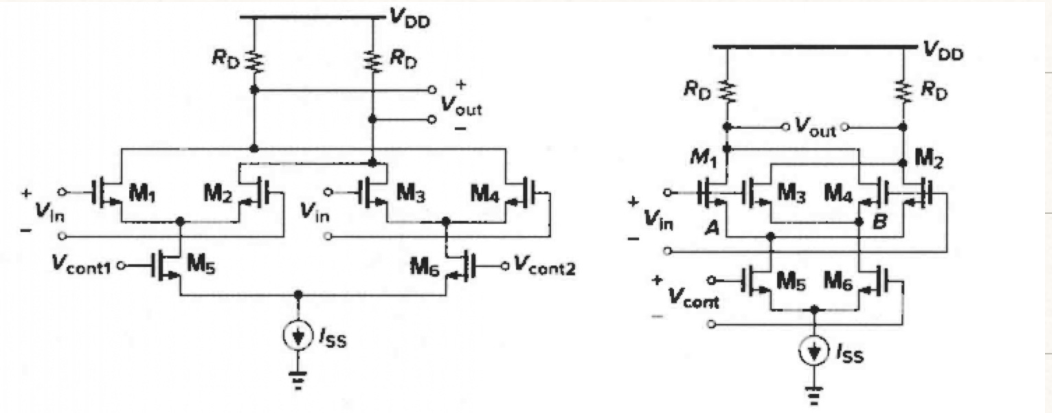
V c o n t V_{cont} Vcont 控制增益,如果 V c o n t V_{cont} Vcont 很大,M6 截止, I D 6 = 0 , I D 3 , 4 = 0 I_{D6}= 0,I_{D3,4}= 0 ID6=0,ID3,4=0, M 1 , M 2 , M 5 M_1,M_2,M_5 M1,M2,M5 构成差动对, V o u t = − g m ⋅ R o Vout= -gm \cdot Ro Vout=−gm⋅Ro;同理 V c o n t Vcont Vcont 很小, V o u t = g m ⋅ R D Vout= gm \cdot R_D Vout=gm⋅RD。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








