MnasNet

1. 轻量化网络的概念

方法	例子
1. 压缩已训练好的模型	知识蒸馏； 权值量化剪枝 (①权重剪枝；②通道剪枝)；注意力迁移
2. 直接训练轻量化网络	SqueezeNet；MobileNets 系列；MnasNet；ShuffleNet 系列；Xception；EfficientNet；EfficientDet
3. 加速卷积运算	im2col + GEMM；Winograd 低秩分解
4. 硬件部署	TensorRT；JetsonTensorflow；slimTensorflow；liteOpenvino；FPGA 集成电路

关键词：参数量、计算量、内存访问量、耗时、能耗、碳排放、CUDA 加速、对抗学习、Transformer、Attention、Nas、嵌入式开发、FPGA、软硬件协同设计、移动端、边缘段、智能终端

2. MnasNet 创新点

1. 多目标优化函数
2. 多层 NAS 搜索空间（准确度性能 + 真实手机推理时间）

这种直接用落地设备比 FLOPs, MAC, Params 要更加合理

2.1 多目标优化函数

$$\underset{m}{\mathrm{maximize}}ACC(m)\times [\frac{LAT(m)}{T}{]}^w$$

其中 $m$ 为模型，$\underset{m}{\mathrm{maximize}}$ 为该模型 $m$ 的优化函数的目标，即使得后面的部分最大化，$ACC(m)$ 为该网络的准确率，$LAT$ 为该网络的实际推理速度，$T$ 为期望网络的推理速度，是一个人为设定的常数，$w$ 被定义为：

$$w=\{\begin{array}{ll}\alpha ,& ifLAT(m)\le T\\ \beta ,& others\end{array}$$

要想使得目标函数足够大，$ACC$ 需要变大，$LAT$ 小，即上面的公式表示：找到某个模型的 $m$ 使得目标函数最大化。

$LAT$ = Latency，即延迟 -> 模型的推理速度

我们看一下这张数据图：

我们分析一下 $\alpha$, $\beta$ 这两个参数：

• 当我们设置 $\alpha =0,\beta =1$ 时：

  • 如果模型的 $LAT$ 满足我们设置的推理速度 $T(LAT(m)\le T)$ ，那么 $w=\alpha =0$ ，模型的 $Acc$ 就是其本身，模型并无任何波澜，甚至想笑😂；
  • 如果模型的 $LAT$ 不满足我们设置的推理速度 $T(LAT(m)\ge T)$，那么 $w=\beta =-1$，此时模型的 $ACC=ACC\times [\frac{T}{LAT(m)}]$ ，很明显 $[\frac{T}{LAT(m)}]\le 1$，所以此时模型的 $ACC=惩罚系数\times ACC$ ，$ACC$ 会降低。且 $LAT$ 越大，惩罚越严重，而损失函数的目的是最大化 $ACC$ ，所以模型会往 $LAT\le T$ 的方向靠拢。

• 当我们设置 $\alpha =-0.07,\beta =-0.07$ 时：

  • 如果模型的 $LAT$ 满足我们设置的推理速度 $T(LAT(m)\le T)$，那么 $w=\alpha =-0.07$，模型的 $ACC=ACC(m)\times [\frac{T}{LAT(m)}{]}^{0.07}\ge 1$，所以模型的 $ACC$ 会被奖励，模型积极向 $T\ge LAT(m)$ 的方向靠拢；
  • 如果模型的 $LAT$ 不满足我们设置的推理速度 $T(LAT(m)\ge T)$，那么 $w=\beta =-0.07$，此时模型的 $ACC=ACC\times [\frac{T}{LAT(m)}{]}^{0.07}\le 1$，所以此时模型的 $ACC = 惩罚系数 \times ACC $，$ACC $会降低。且 $LAT$ 越大，惩罚越严重。

我们会发现，$\alpha =0$, $\beta =1$ 有点像 one-hot 编码；而 $\alpha =-0.07$, $\beta =-0.07$ 则像 label-smooth 编码

通过右图我们也可以看出来，$\alpha =0,\beta =1$ 由于惩罚很激进，所以 $ACC$ 和 $LAT$ 都比较集中；而 $\alpha =-0.07,\beta =-0.07$ 没有那么激进，所以模型没有前者那么集中。

2.1.1 $\alpha$ 和 $\beta$ 的选择

选择 $\alpha =-0.07,\beta =-0.07$ ，优点如下：

• 模型的搜索空间更大
• 可以搜索到更加多样的帕累托最优解（Pareto Optimality），多种速度和精度的权衡（tradeoff）

帕累托最优（Pareto Optimality），也称为帕累托效率（Pareto efficiency），是指资源分配的一种理想状态，假定固有的一群人和可分配的资源，从一种分配状态到另一种状态的变化中，在没有使任何人境况变坏的前提下，使得至少一个人变得更好，这就是帕累托改进或帕累托最优化。

多目标优化函数可以让模型在 $ACC$ 与 $LAT$ 之间做出 tradeoff。

2.2 分层的 NAS 搜索空间

将一个 CNN 分解为 7 个 Block，每个 Block 中的结构是一样的，如 Block2 中的 Layer 2-1 和 Layer 2-N2 是一样的；但每个 Block 之间的结构并不是一样的。这就使得我们可以设计不同的 CNN 模型。

3. NAS 可以设计和搜索出哪些参数呢？

上图中所有蓝色的数字都是由 NAS 设计出来的，如：

• 卷积的方式
• 常规卷积
• 深度可分离卷积
• 逆残差卷积
• 卷积核大小
• 3×3 还是 5×5
• 是否要引入 SE Module
• SE ratio=?
• 跨层连接的方式
• 池化
• 恒等映射
• 无 skip connection
• 输出层卷积核大小
• 每个 Block 中的 Layer 层数

以上这些参数都是由强化学习（Reinforcement Learning, RL）去搜索得到的，这是一个非常庞大的搜索空间，但是在论文中将其预定义为 7 个 Block 的分层的、分解的 搜索空间，这就能够使得不同的 Block 结构是多样化的。

强化学习（Reinforcement Learning, RL），又称再励学习、评价学习或增强学习，是机器学习的范式和方法论之一，用于描述和解决智能体（agent）在与环境的交互过程中通过学习策略以达成回报最大化或实现特定目标的问题

4. NAS 分层的意义

分层的 NAS 搜索可以使得我们的 CNN 模型具有多样性，而不再像以前那样用几个类似的模块去重复堆叠网络，每一个 Block 都可以不一样，充分设计模型。

我们使用分层的 NAS 后，生成的 Block 都不一样了，增加了模型的多样性

5. 强化学习（Reinforcement Learning）

1. 使用 RNN 作为强化学习的智能代理 Agent(Controller)；
2. 它可以采取一系列的行动，从而生成一系列的模型；每生成一个模型就将这个模型训练出来（Trainer）；
3. 获取它的精度（accuracy）并在真实的手机（Mobile phones）上获取它的实测速度（latency）；
4. 由精度和速度算出多目标的优化函数(Multi-objective reward)，就是我们刚才提到的公式；
5. 再由这个函数作为奖励 (reward) 反馈给 RNN 代理（Controller）。

以上就是一个典型的强化学习流程，这个流程的最终目标是使得目标函数（奖励）的期望最大化。用公式简单表示：

$$J=E_p(a_{1:T};\theta )[R(m)]$$

其中，$E_p$ 为期望，$a_{1:T}$ 为一系列结构选择，$\theta$ 为智能体参数，$[\cdot ]$为决定，$R(\cdot )$为目标函数（奖励），$m$ 为模型。

6. 通过 NAS 搜索出来的 MnasNet

新版本

v1版本

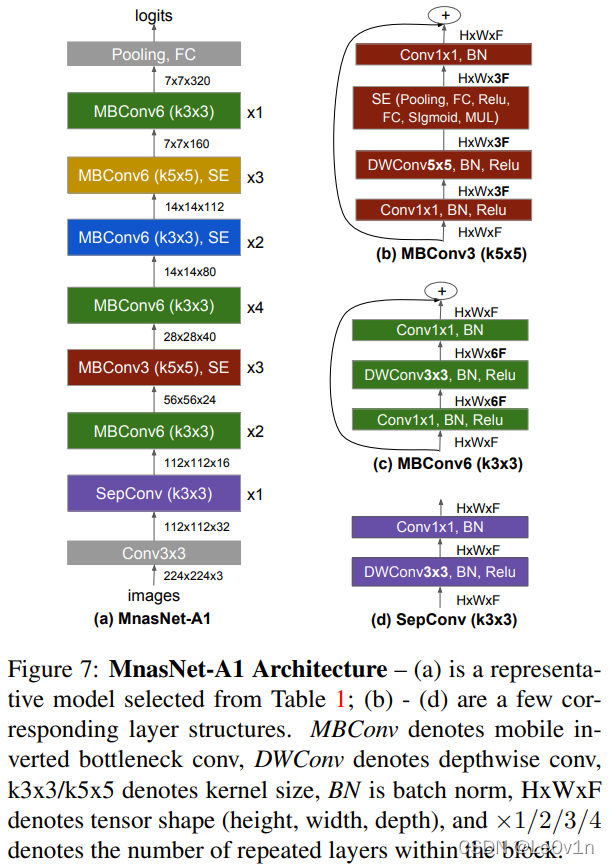
其中：
$\times n$ 表示该 Block 的层数
紫色 为 MobileNet v1 的深度可分离卷积模块
绿色 为 MobileNet v2 的逆残差模块
红色 是加了 SE Attention 的逆残差模块

7. MnasNet 实验结果

7.1 横向对比

7.2 与 MobileNet v2 进行对比

上图表明，MnasNet 速度是 MobileNet v2 的 1.8 倍，性能也是全面超越。

MobileNet v2 可以调节乘宽系数和分辨率大小，从上图中发现，使用了相同的系数，MnasNet 也是全面超越 MobileNet v2 的。

7.3 限制推理时间

上表表明，MnasNet 可以人为设定 $T$，然后根据实际任务搜索出新的网络，通过 NAS 搜索过的网络是要比简单粗暴缩小乘宽系数精度高，速度快！

在 Latency 预算固定的前提下，NAS 的准确率更高

7.4 目标检测

MnasNet 除了可以用于分类网络，也可以作为目标检测网络的 backbone。

下表表明使用了 SE Module 效果会更好（虽然会增加一定的推理时间）：

其中：

• w/o SE: with not SE Module
• w/ SE: with SE Module

7.5 消融实验

为了展示论文的两个创新点（① 多目标的优化函数；② 分层的 NAS）的具体效果，进行了消融实验。

其中：第一行为 base-line 模型（没有 ① 和 ②）。第二行为加了多目标优化函数，速度显著提升，但是牺牲了部分 acc。第三行为加了 ① 多目标优化函数和 ② 分层搜索空间，速度和 acc 都得到了提升。

上表表明本文中的两个技巧是非常有用的。

分层的 NAS 搜索空间实现了不同 Block 的多样化，论文对不同的 Block 进行了 Ablation，下表所示。

下表表明，只用一个相同的 Block 去重复堆叠网络是没有通过分层的 NAS 搜索得到的不同 Block 堆叠出的网络强。

8. 代码讲解

官方代码：https://github.com/tensorflow/tpu/tree/master/models/official/mnasnet

mnasnet_a1 是与论文中的 arch 一一对应。其中：

• r1, r2, …, r3 其实是指 Block 中 Layer 的层数。
• k1, k3, k5 是指该 Block 中卷积核的大小
• s11, s22 指的是横向和纵向的步长（一般二者是一样的）
• e1, e3, e6 指的是 MobileNet v2 中逆残差升维的倍数（e: expand）
• ixx 表示输入通道数
• oxx 表示输出通道数
• noskip 表示该 Block 没有 skip connect 结构
• sexx 表示该 Block 使用 SE Module，且 ratio=xx

9. 总结

1. 以前的 NAS 搜索是以精度为目标的，即 不计一切代价提升精度，而速度和网络大小并不在目标范围内，所以模型过于追求精度。而 MnasNet 将 NAS 搜索的目标从原来的精度扩展到了精度和速度，从而 使得模型在拥有较高精度的条件下，拥有较优的速度。

2. 以前的 NAS 搜索只是搜索出 单一的 Block，然后用这些相同的 Block 去堆叠网络，网络丧失了不同部位的多样性。

PS：NAS 非常消耗算力，穷逼勿扰😂

10. 知识来源

1. 【精读AI论文】谷歌轻量化网络Mnasnet（神经架构搜索）_哔哩哔哩_bilibili
2. 官方代码（TensorFlow）
3. 在 Cloud TPU 上训练 MnasNet
4. PyTorch 复现的 MnasNet
5. 如何评价 Google 最新的模型 MnasNet？
6. MnasNet：终端轻量化模型新思路