子空间投影

参考文章：
[1] https://www.cnblogs.com/seniusen/p/9994177.html
[2] https://blog.csdn.net/xdfyoga1/category_2315349.html

问题：向量 $b=(2,3,4)$ 在 $z$ 轴上和在 $xy$ 平面上的投影是什么，哪个矩阵能产生到一条线上和到一个平面的投影？

1. 投影

当 $b$ 被投影到 $z$ 轴上时，它的投影 $p$ 就是 $b$ 沿着那条线的部分。当 $b$ 被投影到一个平面时，它的投影就是 $b$ 在平面中的部分。

到 $z$ 轴上的投影为 $p1=(0,0,4)$，到 $xy$ 平面上的投影为 $p2=(2,3,0)$，两个投影矩阵 $P1$ 和 $P2$ 分别为

$P1$ 就是选出每个向量的 $z$ 分量， $P2$ 就是选出每个向量的 $x$ 和 $y$ 分量。

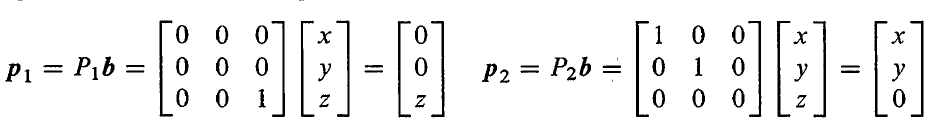
上图中的投影矩阵的作用可以理解为：向量 $b$ 的投影 $p$ 与向量 $b$ 的关系，或通过投影矩阵，可以获得向量 $b$ 的某个投影分量。 （向量 $b$ 经过矩阵 $P1$、$P2$ 后得到了其投影 $p_1$、$p_2$，所以投影是通过矩阵完成的，我们将该矩阵称为投影矩阵）

在这个例子中，$z$ 轴和 $xy$ 平面是正交子空间，就像地面和两面墙的交线一样。

除此之外，它们还是正交补的。整个空间的任意向量都可以表示为它们在两个子空间中分量的和。

2. 到一条线上的投影

假设一条过原点的直线方向为 $a=(a1,a2,\cdots ,am)$，我们要将点 $b=(b1,b2,\cdots ,bm)$ 投影到这条直线上。

将向量 $b$ 投影到向量 $a$ ，$p$ 为 $b$ 在 $a$ 上的投影，即 $p$ 是 $a$ 上离 $b$ 最近的点，$e=b-p$ 这好比 $b$ 与 $p$ 之间的误差，这个误差与 $a$ 相互垂直。

投影 $p$ 和 $a$ 在一条直线上，因此有 $p=\hat{x}a$ （$\hat{x}$ 是一个标量）；误差 $e=b-p=b-\hat{x}a$，然后由 $e$ 垂直于 $a$，我们可得：
$$e\cdot a=0\to (b-\hat{x}a)\cdot a=0\to a\cdot b-\hat{x}a\cdot a=0$$
因此，可求得系数 $\hat{x}$ 为
$$\hat{x}=\frac{a\cdot b}{a\cdot a}=\frac{a^{T}b}{a^{T}a}$$
投影为
$$p=\hat{x}a=\frac{a^{T}b}{a^{T}a}a$$

如果 $b=a$，那么 $\hat{x}=1$，投影还是它自己，$Pb=b$ ；
如果 $b\perp a$，那么 $\hat{x}=0$，投影为 $Pb=0$ 。

第一种就是 $b$ 就在列空间里，投影矩阵为 $I$ ，即相当于不做任何投影；第二种极端情况就是 $b$ 垂直于列空间，此时 $Pb=0$ ，一般情况下向量会有一分量在列空间里，另一分量与列空间垂直，因此投影完成的功能就是去掉垂直部分，保留另一部分。

---

将投影重写为
$$p=a\hat{x}=a\frac{a^{T}b}{a^{T}a}=\frac{a{a}^T}{a^{T}a}b$$
因此，投影矩阵为
$$P=\frac{a{a}^T}{a^{T}a}$$

可以看出：

投影矩阵的性质：

1. 如果向量 $a$ 变为两倍，投影矩阵 $P$ 不变，它还是投影到 $p$；若 $b$ 变成了两倍，投影 $p$ 也会变成2倍；
2. 用任何向量 $b$ 乘以投影矩阵 $P$，结果总在投影矩阵的列空间里。
   因为 $b$ 给出了对其列的线性组合，而我们又知道任何向量 $b$ 乘以投影空间总在向量 $a$ 上，因此投影矩阵 $P$ 的列空间，是通过 $a$ 的一条线，列空间维数是1，投影矩阵的秩是1；
3. 投影矩阵是对称的，因为 $(a{a}^T{)}^T=a{a}^T$；
4. 如果投影矩阵平方，那就是进行两次投影，和进行一次投影是一样的结果，因此有 $P^2=P$。

---

同时，$I-P$ 也是一个投影矩阵，$(I-P)b=b-p=e$。当 $P$ 投影到一个子空间时，$I-P$ 投影到和它垂直的另一个子空间。

3. 到子空间的投影

假设 $n$ 个 $R_m$ 空间中的向量 $a1,\cdots ,an$ 是线性不相关的，我们想找到一个线性组合 $p={\hat{x}}_1{a}_1+\cdots +{\hat{x}}_n{a}_n$ 使得 $p$ 距离一个给定向量 $b$ 最近。

$a1,\cdots ,an$ 可以看做是矩阵 $A$ 的列，我们要找的线性组合是在矩阵 $A$ 的列空间中。我们要找的是距离 $b$ 最近的一个组合 $A\hat{x}$，也就是 $b$ 在列空间的投影。

对上图中红框内的公式进行说明：它解释的是 "我们要找的是距离 $b$ 最近的一个组合 $A\hat{x}$，也就是 $b$ 在列空间的投影 " 这句话。第二个等式借用了上面推出来的投影矩阵的表达式。$A\hat{x}$，则投影矩阵是关于 $A$ 的。

---

同理，误差 $e=b-A\hat{x}$ 垂直于子空间，也就是垂直于子空间的所有向量。

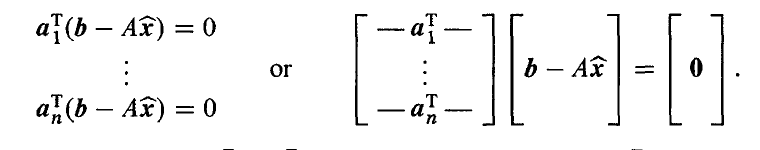
也即
$$A^T(b-A\hat{x})=0\to A^{T}A\hat{x}=A^{T}b$$
$A^{T}A$ 是一个 n×n 的矩阵，因为 $A$ 的列是线性不相关的，所以其是可逆的。可得线性组合系数为
$$\hat{x}=(A^{T}A{)}^{-1}{A}^{T}b$$
所以有，投影和投影矩阵分别为
$$p=A\hat{x}=A(A^{T}A{)}^{-1}{A}^{T}b$$$$P=A(A^{T}A{)}^{-1}{A}^T$$
由 $A^T(b-A\hat{x})=0$ 可知，误差 $e$ 位于 $A$ 的左零空间 $N(A^T)$ 中，向量 $b$ 被分为了投影 $p$ 和误差 $e$ 两部分。

$A^{T}A$ 是可逆的当且仅当 $A$ 的列是线性不相关的。

当 $Ax=0$ 时，我们有 $A^{T}Ax=0$ 。而当 $A^{T}Ax=0$ 时，我们有
$$x^T{A}^{T}Ax=0\to (Ax{)}^{T}Ax=0\to Ax=0$$
因此 $A^{T}A$ 和 $A$ 有着一样的零空间，当 $A$ 的列线性不相关时，$A^{T}A$ 是一个方阵，对称并且可逆。

---

这里有另一种说法，更好理解。
参考：https://blog.csdn.net/xdfyoga1/article/details/37568067

4. 二维空间 $R^2$ 推广到高维空间 $R^n$ 的情况

在这之前，我们需要讨论一下为什么要投影?

• $Ax=b$ 无解，当无解时我们只能求解最接近的那个可解问题来求原方程的最优解，即要将 $b$ 作调整，使其变成 $A$ 的列空间中最接近 $b$ 的那个向量。

那么怎样才算是最接近的呢？

• 这就要将 $b$ 向 $A$ 的列空间投影得到 $p$ ，因为 $p$ 在列空间中，因此 $Ax=p$ 是有解的，这就是为什么要作投影，可以用来解决方程无解的情况。

为了理解方便，接下来我主要以三维情况为例，但是要知道更高维和三维本质上是一样的。

假设有三维中的一个平面和一个不在平面上的向量 $b$ ，现在要将 $b$ 投影在平面上，平面有两个基向量 $a_1$ 和 $a_2$ ，它们线性无关，回想下和方程组的联系，可知这个平面是矩阵 $A$ 的列空间，即 $A=\left[\begin{array}{cc}{a}_1& a_2\end{array}\right]$，当然矩阵 $A$ 可以是两列，也可以是 $n$ 列，这里写成两列，投影 $p$ 是基向量的组合，即 $p={\hat{x}}_1{a}_1+{\hat{x}}_2{a}_2$ ，写成矩阵的形式即 $p=A\hat{x}$ ，根据误差向量 $e=b-A\hat{x}$ 垂直于平面，我们可得出等式，$e$ 垂直于平面的意思就是 $e$ 分别垂直于两个基向量 $a_1$ 和 $a_2$ ，因此分别得到
$$a_1^T(b-A\hat{x})=0$$ $$a_2^T(b-A\hat{x})=0$$
将两个方程合并成矩阵形式：
$$\left[\begin{array}{c}{a}_1^T\\ a_2^T\end{array}\right](b-A\hat{x})=\left[\begin{array}{c}0\\ 0\end{array}\right]$$ 即，$$A^T(b-A\hat{x})=0$$ 对比可发现平面上的投影方程和直线上的投影方程很相似，同样对其进行变形，将其改写为
$$A^{T}A\hat{x}=A^{T}b$$ $$\hat{x}={\left(A^{T}A\right)}^{-1}{A}^{T}b$$
投影和投影矩阵分别为
$$p=A\hat{x}=A{\left(A^{T}A\right)}^{-1}{A}^{T}b$$ $$P=A{\left(A^{T}A\right)}^{-1}{A}^T$$ 这个公式看起来很复杂，根据乘积的逆等于各自逆的反顺序相乘，可得到
$$P=A{A}^{-1}(A^T{)}^{-1}{A}^T=I$$

问题出现了，为什么会这样呢？不应该投影矩阵算出来始终为I的，一定要注意因为 $A$ 不是方阵（我们讨论的是 $Ax=b$ 无解的情况，因此A不是方阵），所以A的逆不存在，所以 $$P=A{\left(A^{T}A\right)}^{-1}{A}^T$$ 不能化简，我们做的这种变换是不成立的，只有 $A$ 为可逆阵时才允许做后面的这一步变换。

我们可以看一下当 $A$ 是可逆阵时这个式子表示的含义：如果 $A$ 是 $n\ast n$ 可逆方阵，那么它的列空间是整个 $R_n$ ，因为其对于所有的 $b$ 均有解，既然 $b$ 已经在列空间中，那么投影矩阵 $P$ 是单位阵也无可厚非了。

投影矩阵的性质：

1. 投影矩阵仍然是对称阵，将P进行转置即可得出结论；
2. $P^2=P$，即进行第二次投影时还是会投影在第一次投影的地方。

应用

投影思想在最小二乘法中的应用

当我们遇到一个方程组，有太多的方程，未知数却只有几个，现在我们要求它的最优解。假设有三个点（1,1），（2,2），（3,2），这三个点拟合直线 $b=C+Dt$，首先我们要建立矩阵 $A$ ，只要找到 $A$ ，我们就能使用上面推导的那些公式，$C+D=1$，$C+2D=2$，$C+3D=2$，所以对于这个例子，对应的无解方程 $Ax=b$ 为
$$\left[\begin{array}{cc}1& 1\\ 1& 2\\ 1& 3\end{array}\right]\left[\begin{array}{c}C\\ D\end{array}\right]=\left[\begin{array}{c}1\\ 2\\ 2\end{array}\right]$$

所谓的最优解并不是这个方程的解，而是 $Ax=p$ 的解，即 $$A^{T}A\hat{x}=A^{T}b$$ 的解。

---

附推导过程：
$$p=A\hat{x}=A\hat{x}=A(A^{T}A{)}^{-1}{A}^{T}b=Ax$$ $$\to (A^{T}A{)}^{-1}{A}^{T}b=x$$ $$\to A^{T}Ax=A^{T}b$$

---

解法1：线性代数方法来求解CD

由于
$$A^{T}A=\left[\begin{array}{ccc}1& 1& 1\\ 1& 2& 3\end{array}\right]\left[\begin{array}{cc}1& 1\\ 1& 2\\ 1& 3\end{array}\right]=\left[\begin{array}{cc}3& 6\\ 6& 14\end{array}\right]$$

$$A^{T}b=\left[\begin{array}{ccc}1& 1& 1\\ 1& 2& 3\end{array}\right]\left[\begin{array}{c}1\\ 2\\ 2\end{array}\right]=\left[\begin{array}{c}5\\ 11\end{array}\right]$$

可以解出 $\hat{x}=\left[\begin{array}{c}C\\ D\end{array}\right]=\left[\begin{array}{c}\frac{2}{3}\\ \frac{1}{2}\end{array}\right]$ 。

---

解法2：微积分求解CD

其误差为 $e=b-p=b-Ax$ 。

最小化误差函数：
$$\begin{array}{rl}e& =e_1^2+e_2^2+e_3^2\\ & =(b_1-p_1)+(b_2-p_2)+(b_3-p_3)\\ & =(C+D-1{)}^2+(C+2D-2{)}^2+(C+3D-2{)}^2\end{array}$$

对该式求偏导，最终得到
$$\{\begin{array}{c}3C+6D=5\\ 6C+14D=11\end{array}\to \{\begin{array}{c}C=\frac{2}{3}\\ D=\frac{1}{2}\end{array}$$

---

综上，最优直线是 $y=2/3+1/2t$，由此三个点在线上的投影为 $p1=7/6$，$p2=5/3$，$p3=13/6$ （不是垂直投影），各点的误差为$e1=-1/6$，$e2=2/6$，$e3=-1/6$ 。

$b$，$p$ 和 $e$ 之间满足 $b=p+e$ ， $e$ 不仅垂直于 $p$ ，同时还垂直于其他向量， $e$ 垂直于整个列空间。