动态规划：建造楼梯

一个好奇的小孩有N块砖，他要用这N块砖建造不同的楼梯。楼梯各个台阶的砖块数不同，但必须严格地递减。每个楼梯至少包含两个台阶，并且每个台阶至少包含一块砖。下图是5块砖的楼梯。
输入样例：
输入砖块数N：5
样例输出：
一共有2种不同的建构方法

分析：可以看成一种整数划分情况 例如 5分为4+1，3+2两种情况
划分条件：
1.后面的数小于前面的数 底砖要大于上面的砖

利用动态规划的方法解决问题
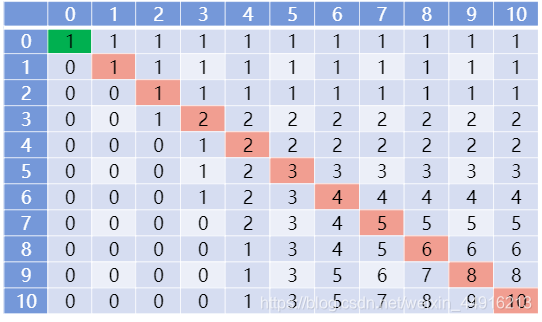
动态转移方程 f(m,n)表示由n块砖组成楼梯，最后一行楼梯砖不超过m的方案总数 f(m,n)=f(m-1,n-m)+f(m-1,n)
边界： f(0,0)=1
建表结果：

answer:

#include<iostream>

using namespace std;


int main()
{
	int n;
	cout<<"输入砖块数N：";
	cin>>n;
	n=n+1;
	int f[n][n];
	f[0][0]=1;
	for(int i=0;i<n;i++)
	{
		
		for(int j=1;j<=i;j++)
		{
			f[i][0]=0;
			
			//i块砖最后一行楼梯砖不超过j的方案书数 
			f[i][j]=f[i][j-1]+f[i-j][j-1]; 
		}
		for(int j=i+1;j<n;j++)
		{
			f[i][j]=f[i][i];
		}
	}
	printf("一共有%d种不同的构建方法",f[n-1][n-1]-1);
	return 0;
}