基于Numpy与反向传播的手写体识别

一、 问题描述

还是做手写体识别，但相较于实验五，升级的地方在于多了网络层的封装以及在梯度下降时用上反向传播来提交代码的可复用性和训练效率。

二、 设计简要描述

机器学习的三个基本步骤——

程序设计思路——(此图放大可看清)

三、程序清单

import numpy as np
from mnist import load_mnist
from collections import OrderedDict  # 有序字典，记录传入变量的顺序，更好实现值的传播


class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        # 获取x数组中小于0的元素的索引
        self.mask = (x <= 0)  # self.mask是一个数组（大于0的为False,小于0的为True）
        out = x.copy()  # out变量表示要正向传播给下一层的数据，即上图中的y
        out[self.mask] = 0  # 将为True的值改为0

        return out

    def backward(self, dout):
        dout[self.mask] = 0  # 如果正向传播的输入值小于等于0，则反向传播的值等于0
        dx = dout
        return dx


class Linear:
    def __init__(self, W, b):
        self.W = W  # 权重参数
        self.b = b  # 偏置参数
        self.x = None  # 用于保存输入数据
        # 定义成员变量用于保存权重和偏置参数的梯度
        self.dW = None
        self.db = None

    # 全连接层的前向传播
    def forward(self, x):
        # 保存输入数据到成员变量用于backward中的计算
        self.x = x
        # 请补充代码求全连接层的前向传播的输出保存到变量out中
        out = self.x.dot(self.W) + self.b

        return out

    # 全连接层的反向传播
    def backward(self, dout):
        # 请同学补充代码完成求取dx,dw,db，dw,db保存到成员变量self.dW,self.db中
        dx = dout.dot(self.W.T)
        self.dW = self.x.T.dot(dout)
        self.db = np.sum(dout, axis=0)
        return dx


# softmax函数
def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a, axis=1, keepdims=True)
    y = exp_a / sum_exp_a
    return y


# 损失函数
# y是神经网络的输出，t是正确解标签
def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))


class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None  # softmax的输出
        self.t = None  # 监督数据

    # SoftmaxWithLoss层的前向传播函数
    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)

        return self.loss

    # SoftmaxWithLoss层的反向传播函数
    def backward(self, dout=1):
        # 请补充代码完成求取SoftmaxWithLoss层的反向传播的输出
        # 注意：反向传播时将要传播的值除以批的大小，传递给前面层的是单个数据的误差
        batch_size = self.t.shape[0]  # 取出批数据的数量
        dx = (self.y - self.t) / batch_size  # 计算出单个数据的误差

        return dx


class TwoLayerNet:
    # 模型初始化
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        # 初始化权重
        self.params = {}
        # 获取第一层权重和偏置
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        # 获取第二层权重和偏置
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

        # 生成层
        # 将神经网络的层保存为有序字典OrderedDict
        self.layers = OrderedDict()
        # 添加第一个全连接层到有序字典中
        self.layers['Linear1'] = Linear(self.params['W1'], self.params['b1'])
        # 激活函数层
        self.layers['relu'] = Relu()
        # 第二个全连接层
        self.layers['Linear2'] = Linear(self.params['W2'], self.params['b2'])

        # 将SoftmaxWithLoss类实例化为self.lastLayer
        self.lastLayer = SoftmaxWithLoss()

    # 识别函数调用每个层的向前传播的函数，并且把输出作为下一个层的输入
    # 通过前向传播获取预测值
    def predict(self, x):
        # 遍历有序字典
        for layer in self.layers.values():
            # 请补充代码完成神经网络层的前向传播
            x = layer.forward(x)
        return x

    # x:输入数据, t:监督数据
    def loss(self, x, t):
        # 获取预测值
        y = self.predict(x)
        # 返回损失
        return self.lastLayer.forward(y, t)

    # 求精度
    def accuracy(self, x, t):
        y = self.predict(x)
        # 获取预测概率最大元素的索引和正确标签的索引
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    # 求梯度
    def gradient(self, x, t):
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        # 求最后SoftmaxWithLoss层的反向传播输出
        dout = self.lastLayer.backward(dout)

        # 从后往前遍历有序字典
        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            # 获取正在被遍历的层的反向传播输出
            dout = layer.backward(dout)

        # 设定
        grads = {}
        # 获取第一层网络参数的梯度
        grads['W1'], grads['b1'] = self.layers['Linear1'].dW, self.layers['Linear1'].db
        # 获取第二层网络参数的梯度
        grads['W2'], grads['b2'] = self.layers['Linear2'].dW, self.layers['Linear2'].db
        return grads


if __name__ == '__main__':
    # 获得MNIST数据集
    (x_train, t_train), (x_test, t_test) = load_mnist(one_hot_label=True)

    # 定义训练循环迭代次数
    iters_num = 2000
    # 获取训练数据规模
    train_size = x_train.shape[0]
    # 定义训练批次大小
    batch_size = 100
    # 定义学习率
    learning_rate = 0.1


    # 计算一个epoch所需的训练迭代次数（一个epoch定义为所有训练数据都遍历过一次所需的迭代次数）
    iter_per_epoch = 1
    MyTwoLayerNet = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)  # 实例化TwoLayerNet类创建MyTwoLayerNet对象
    #训练循环的代码
    for i in range(iters_num):
        # 在每次训练迭代内部选择一个批次的数据
        batch_choose = np.random.choice(train_size, batch_size)  # choice()函数的作用是从train_size中随机选出batch_size个
        x_batch = x_train[batch_choose]
        t_batch = t_train[batch_choose]

        # 计算梯度
        grad = MyTwoLayerNet.gradient(x_batch, t_batch)
        # 更新参数
        for params in ('W1', 'b1', 'W2', 'b2'):
            MyTwoLayerNet.params[params] -= learning_rate * grad[params]


        loss = MyTwoLayerNet.loss(x_batch, t_batch)


        # 判断是否完成了一个epoch，即所有训练数据都遍历完一遍
        if i % iter_per_epoch == 0:
            train_acc = MyTwoLayerNet.accuracy(x_train, t_train)
            test_acc = MyTwoLayerNet.accuracy(x_test, t_test)
            # 输出一个epoch完成后模型分别在训练集和测试集上的预测精度以及损失值
            print("iteration:{} ,train acc:{}, test acc:{} ,loss:{}".format(i, round(train_acc, 3), round(test_acc, 3),  round(loss, 2)))  

四、结果分析

本次实验与上次实验相比用上了反向传播算法，计算速度上快了许多，大约只用了7、8分钟就运行了2000轮；效率上也高很多，2000轮时精确度基本稳定在94%。足见方法正确的重要性。

项目目录结构

五、调试报告

1. 第一次运行遇到的问题说mnist库的main函数无法调用，但查看解释器明明已经导入该库，对照上一次实验发现是缺少mnist.py文件。
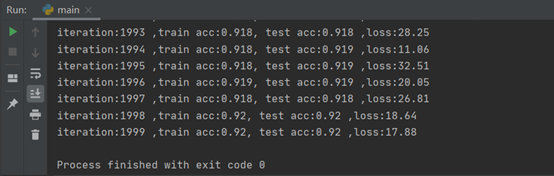
2. 在构建网络时开始没有主要到加入第二个全连接层之前要先加入Relu激活层，对比加入前后的结果发现，同样是训练2000轮，没加激活层的网络精确度最后大约在0.92(如下图所示)，加入激活层后，精确度最后大约在0.94(见“结果分析”)。
   

六、实验小结

收获：

1. 学到了计算图的概念，今后在写含有复杂公式代码时可以尝试自己画
2. 确定反向传播公式的两把利剑:①链式法则 ②矩阵的形状
3. 在Relu激活层由于反向传播时对于正向输入小于0的输入要让信号停在此处(即让其为0)，这里巧妙地应用了self.mask数组，先将所有正向输入小于0的设置为True，再让所有值为True的等于0。
4. 另外此次实验将不同的网络层进行了封装，再结合有序字典OrderedDict，这样做提升了代码的可维护性和可复用性，可以很轻松地搭建网络。