Matlab 实现图像的直角坐标系和极坐标系的相互转化

某日需要在matlab进行图像的的极直互化，发现并没有介绍相应内容的文章，所以有了自己调研一下并写一写的想法。果然只要想就能做到，所以有了下面这篇文章。

根据直角坐标系（笛卡尔系）内数值和极坐标系关系

根据上述公式不难想出，在直角坐标系中的圆会在极坐标中转化为一条直线（画图太麻烦了，脑补吧）。

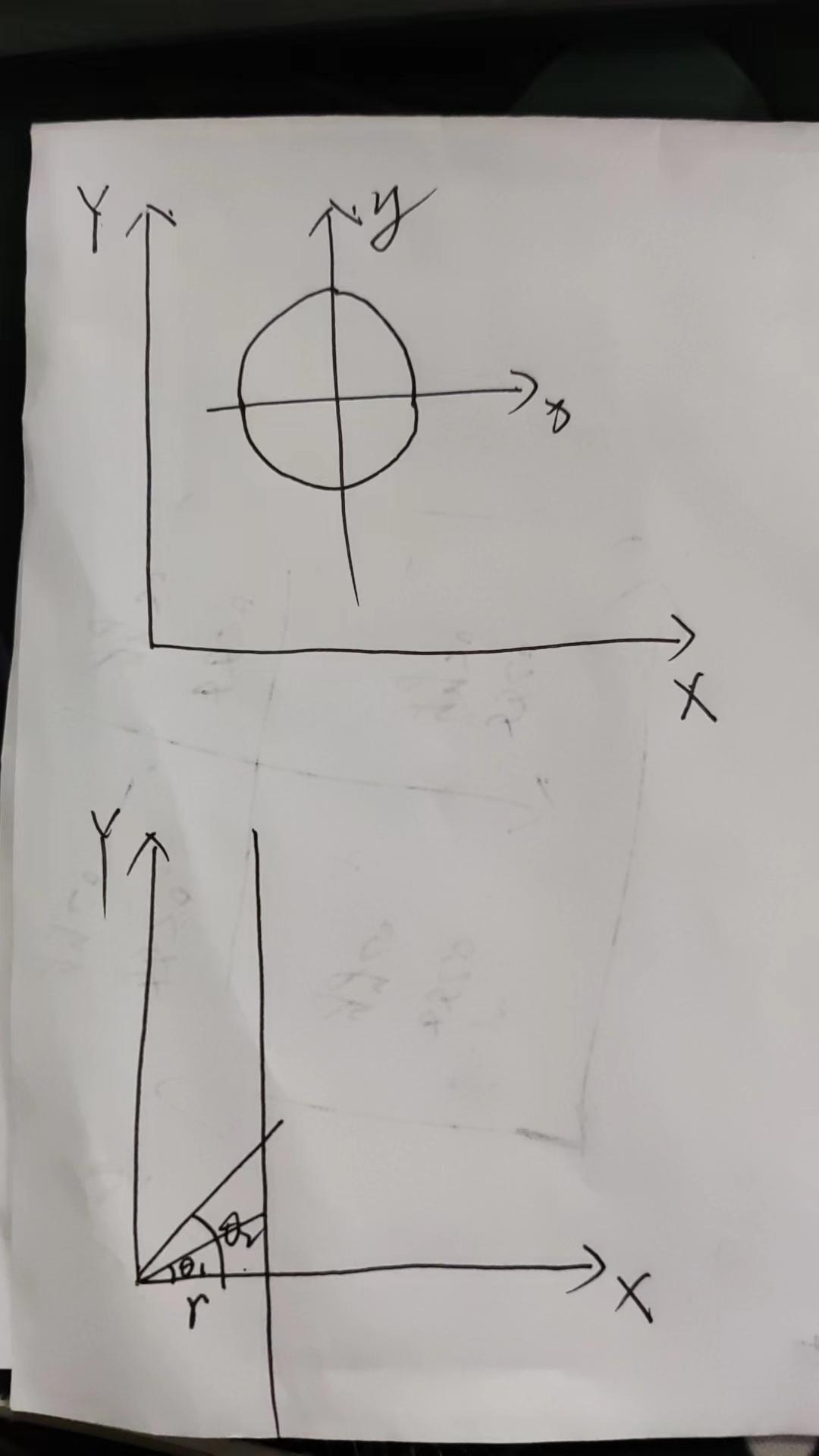
还是画一下吧便于理解，就图上这样XY代表的大坐标系，即最后生成图像的坐标系，里面小的坐标系呢，上面图表示的是直角系，下面图表示的是极坐标系，即求二者之间的互相转化。

直角系到极坐标系的转化步骤是，算出极坐标系点位在直角系中点位的映射（由于我都极坐标系尺寸更大，所以还需要进行插值，这里用到的双线性插值）（这里映射是指的外部的大坐标系）

双线性插值的知识很多，很容易找到大家去找吧。

clear;
clc;
%自己命名的读取函数
% I=readOriginalImage('D:\MatlabWorkPlace\MatlabCode\PolarAndCartesian\512circle.txt',512,512);
I=readSingleRecon('E:\DeadMouse\5\OriginalImage\0015.txt',353,353);
imtool(I,[]);

[M,N]=size(I);
R=M/2;
X=353;
Y=353*2;
delta_r=R/X;
delta_theta=2*pi/Y;
Image=zeros(Y,X);
theta_1=zeros(1,Y);
for i=1:Y
    theta=i*delta_theta;
    theta_1(1,i)=theta;
    sin_theta=sin(theta);
    cos_theta=cos(theta);
    for j=1:X
        temp_r=j*delta_r;
        x= R+temp_r*cos_theta;
        xf=floor(x);
        xc=ceil(x);
        if xf<1
            xf=1;
        end
        if xc<1
            xc=1;
        end
        if xc>M
            xc=M;
        end
        y= R+temp_r*sin_theta;
        yf=floor(y);
        yc=ceil(y);
         if yf<1
            yf=1;
         end
        if yc<1
            yc=1;
        end
        if yc>N
            yc=N;
        end
        Aaa=interp_bilinear(I,xf,xc,x,yf,yc,y);
        Image(i,j)=interp_bilinear(I,xf,xc,x,yf,yc,y);
    end
end
imtool(Image,[]);
% I=xRemoveStripesVertical(Image,6,'db25',7);
I=Image;
imtool(I,[]);
%自己命名的保存函数
saveFile('D:\MatlabWorkPlace\MatlabCode\PolarAndCartesian.txt',I);


%双线性插值代码
function value=interp_bilinear(I,x1,x2,x,y1,y2,y)
    if x2==x1&&y2==y1
        value=I(x1,y1);
    elseif x2==x1
        value=I(x1,y1)*(y2-y)/(y2-y1)+I(x1,y2)*(y-y1)/(y2-y1);
    elseif y1==y2
        value=I(x1,y1)*(x2-x)/(x2-x1)+I(x2,y1)*(x-x1)/(x2-x1);
    else
         h=(x2-x1)*(y2-y1);
        value=I(x1,y1)*(x2-x)*(y2-y)/h+I(x2,y1)*(x-x1)*(y2-y)/h+I(x1,y2)*(x2-x)*(y-y1)/h+I(x2,y2)*(x-x1)*(y-y1)/h;
    end
end

极坐标系到直角系同样的，算出直角系中的点位在极坐标系中的映射（映射指的是外部的大坐标系）

clear;
%自己命名的读取
I=readSingleRecon('D:\MatlabWorkPlace\MatlabCode\PolarAndCartesian.txt',353*2,353);
imtool(I,[]);
[Y,X]=size(I);
R=353/2;
M=2*R;
N=2*R;
delta_r=R/X; 
delta_theta=2*pi/Y;
Image=zeros(M,N);
theta_1=zeros(M,N);
for i=1:M
    for j=1:N
        xx=i-R;
        yy=j-R;
        temp_r=sqrt((xx)^2+(yy)^2);
        r=temp_r/delta_r;
        r=round(r);
        if xx==0
            xx=0.0001;
        end
        if xx>0 && yy>0
            theta=atan(yy/xx);
        elseif xx<0 &&yy>0
            theta =atan(yy/xx)+pi;
        elseif xx<0 &&yy<0
            theta=atan(yy/xx)+pi;
        elseif xx>0 &&yy<0
            theta=atan(yy/xx)+2*pi;
        end
        theta=theta/delta_theta;
        theta=round(theta);
        if theta==0
            theta=1;
        end
        if theta>Y
            theta=Y;
        end
         if r>X
            r=X;
        end
        Image(i,j)=I(theta,r);
        
    end
end
imtool(Image,[]);

无论是直角系转化为极坐标系，还是极坐标系转化为直角系，最重要的就是映射关系的对应

结果贴上

原图

转化成极坐标系

极坐标系转化为直角系

结论如下

可以看到经过转化，内切圆内区域并没有发生什么变化，内切圆外区域又没什么用（差别是因为两次转化造成的），证明这个计算过程是可行的。代码水平一般将就看吧。