AcWing算法基础课第四讲动态规划(1): 背包问题

已于 2023-08-23 01:39:02 修改
阅读量520 收藏 1
点赞数 3
分类专栏： AcWing算法基础课笔记 文章标签： 算法 动态规划
于 2023-03-13 19:24:34 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_45029883/article/details/129495639
版权

文章目录

1. 01背包问题

通过例子进行讲解：
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。
接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0<N,V≤1000
0<vi,wi≤1000

输入样例：
4 5
1 2
2 4
3 4
4 5

输出样例：
8

解题思路：
Alt
如图所示，将背包问题状态表示为f[i][j]，其含义为从前i个物品中选择物品，选择的物品总体积V总 <= j，所选择的物品总价值最大值就是f(i,j)。
在状态计算时，可将状态集合进行划分，划分为不包含第i种物品的最大价值f[i - 1][j]和包含第i种物品的最大价值f[i - 1][j - v[i]] + w[i]，最后将两者进行比较，即可求得最终的f[i][j]。

  • 朴素做法：
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++) {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    return 0;
}

可以发现，f[i][j]只与f[i-1][j]和f[i-1][j-v[i]]相关，前i种物品的状态选择可以用前i-1种物品的状态来表示，所以我们可以将f[i][j]的二维状态优化为一维状态进行表示。

  • 优化做法：
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--) {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    cout << f[m] << endl;
    return 0;
}

注意⚠️：这里进行优化时，在循环的过程中，我们需要将j初始化为m，从大到小进行遍历，这样循环体中的f[j - v[i]]就相当于f[i - 1][j - v[i]]。

2. 完全背包问题

通过例子进行讲解：
有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。
第 i 种物品的体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。
接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 种物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0<N,V≤1000
0<vi,wi≤1000

输入样例
4 5
1 2
2 4
3 4
4 5

输出样例
10

解题思路：
完全背包问题对于每种物品的个数没有限制，在背包体积大小固定队情况下选择物品，所选物品的总体积不能超过背包体积，使得所选物品的总价值最大。
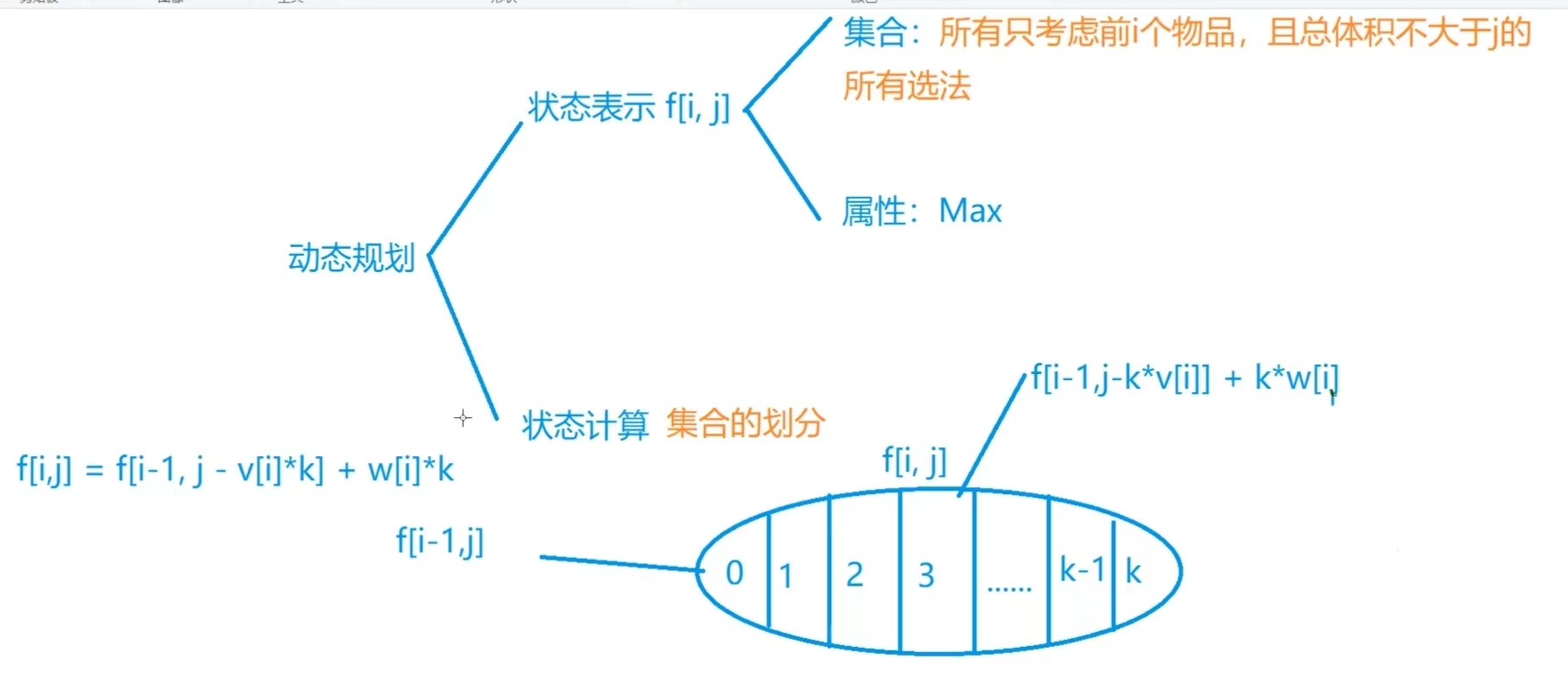
请添加图片描述
在这里进行状态计算时，将该状态下的集合进行划分为包含0件第i种物品的总价值最大值、包含1件第i种物品的总价值最大值、包含2件第i种物品的总价值最大值，依此类推，包含k件第i种物品的总价值最大值，通过将集合进行划分，求得每种情况下价值的最大值，最后比较，即可得到最终的价值最大值。

  • 朴素做法：
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
            for (int k = 0; k * v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + w[i] * k);
    cout << f[n][m] << endl;
    return 0;
}

对于完全背包问题，同样可以将状态从二维优化为一维，如下所示：
请添加图片描述

  • 优化做法：
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = v[i]; j <= m; j ++ )
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

3. 多重背包问题

（1）多重背包问题 I

有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。
接下来有 N 行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式
输出一个整数，表示最大价值。

数据范围
0<N,V≤100
0<vi,wi,si≤100

输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例
10

解题思路：
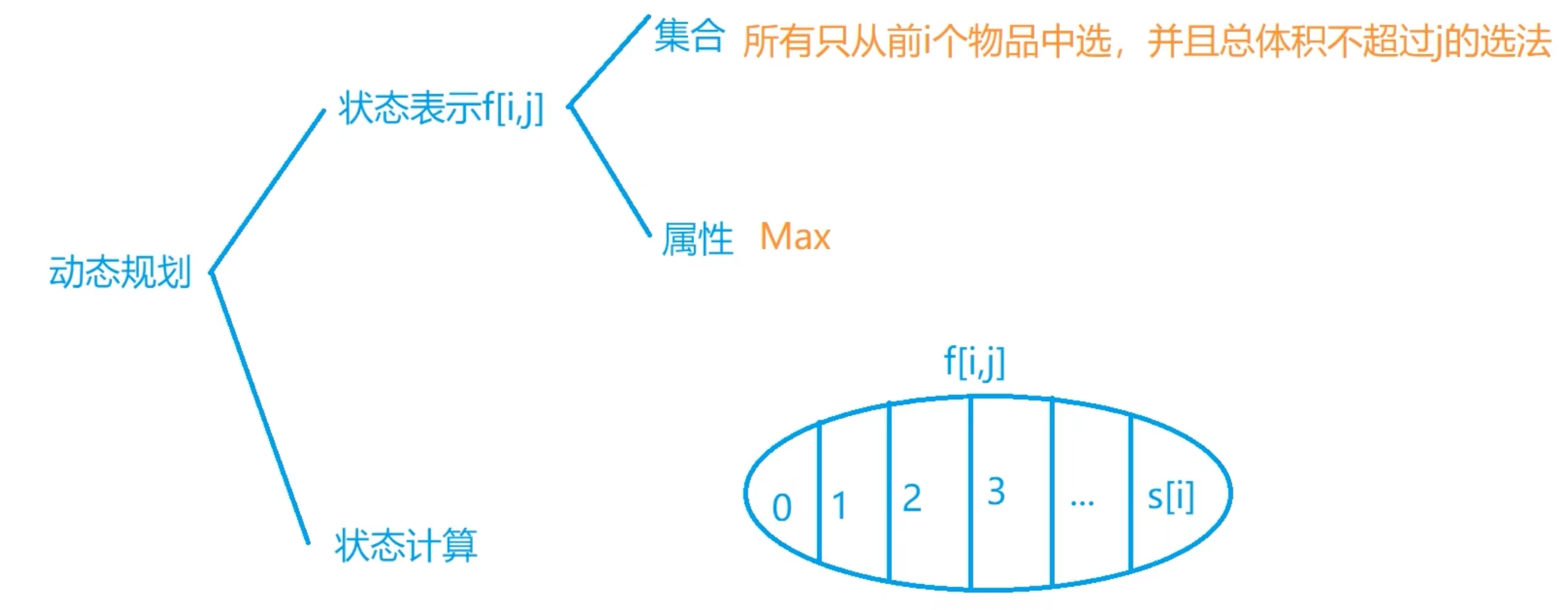
在这里插入图片描述

多重背包问题限制每件物品的个数为si，在背包体积大小固定的情况下选择物品，所选物品的总体积不能超过背包体积，使得所选物品的总价值最大。
此时使用f[i][j]表示前i种物品总体积不超过j的情况下的总价值最大值。
f[i][j]可表示为f[i][j] = max(f[i - 1][j - v[i] * k] + w[i] * k); 其中k = 0, 1, 2, ... , s[i]

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N], s[N];
int f[N][N];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
    
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
            for (int k = 0; k * v[i] <= j && k <= s[i]; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
    cout << f[n][m] << endl;
    return 0;
}

多重背包问题同样可进行优化，在上边讲解中，需要考虑第i种物品取1, 2, 3, ... , s[i]，其实可以进行二进制优化，把每种物品进行二进制划分，比如第i种物品可分别划分为1, 2, 4, 8, … , 2k, c，其中c<2k+1，也就是说将第i种物品进行重新打包，每个包裹里有1件、2件、4件等等。通过以上操作，将每件物品都进行打包后，可以把多重背包问题转化为01背包问题，因为打包后的第i种物品进行组合后，可以得到0~s[i]件中任意件物品。

（2）多重背包问题 II

有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。
接下来有 N 行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式
输出一个整数，表示最大价值。

数据范围
0<N≤1000
0<V≤2000
0<vi,wi,si≤2000

提示：
本题考查多重背包的二进制优化方法。

输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例
10

代码如下：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 12010, M = 2010;

int n, m;
int v[N], w[N];
int f[M];

int main()
{
    cin >> n >> m;

    int cnt = 0; //将多重背包问题映射为01背包问题
    for (int i = 1; i <= n; i ++ )
    {
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while (k <= s)
        {
            cnt ++ ;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if (s > 0)
        {
            cnt ++ ;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }

    n = cnt;

    for (int i = 1; i <= n; i ++ )
        for (int j = m; j >= v[i]; j -- )
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

4. 分组背包问题

通过例子进行讲解：

有 N 组物品和一个容量是 V 的背包。
每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 vij，价值是 wij，其中 i 是组号，j 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行有两个整数 N，V，用空格隔开，分别表示物品组数和背包容量。
接下来有 N 组数据：
每组数据第一行有一个整数 Si，表示第 i 个物品组的物品数量；
每组数据接下来有 Si 行，每行有两个整数 vij,wij，用空格隔开，分别表示第 i 个物品组的第 j 个物品的体积和价值；

输出格式
输出一个整数，表示最大价值。

数据范围
0<N,V≤100
0<Si≤100
0<vij,wij≤100

输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5

输出样例
8

解题思路：
分组背包问题限制同一组物品最多只能选一个，在背包体积大小固定的情况下分组选择物品，所选物品的总体积不能超过背包体积，使得所选物品的总价值最大。如下图所示：
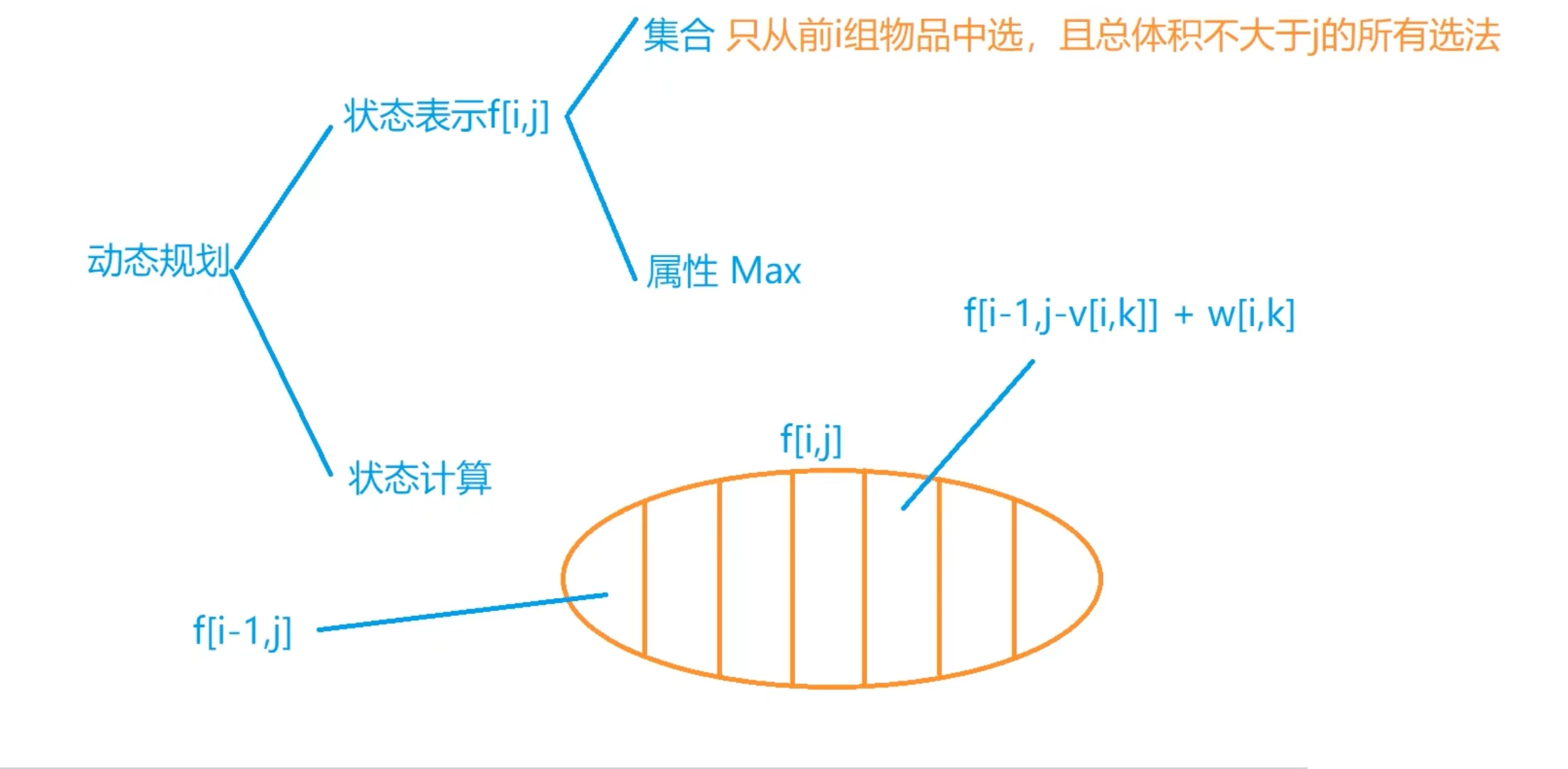
请添加图片描述
在这里进行状态计算时，从前i组中进行选择的集合可划分为不选择第i组物品的总价值最大值、包含第i组第1个物品的总价值最大值、包含第i组第2个物品的总价值最大值，依此类推，包含第i组第k个物品的总价值最大值，通过将集合进行划分，求得每种情况下价值的最大值，最后比较，即可得到最终的价值最大值。

代码如下：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N];
int f[N];

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ )
    {
        cin >> s[i];
        for (int j = 0; j < s[i]; j ++ )
            cin >> v[i][j] >> w[i][j];
    }

    for (int i = 1; i <= n; i ++ )
        for (int j = m; j >= 0; j -- )
            for (int k = 0; k < s[i]; k ++ )
                if (v[i][k] <= j)
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

    cout << f[m] << endl;

    return 0;
}

参考资料：AcWing的算法基础课
链接：https://www.acwing.com/blog/content/277/

程序员小浩
关注
  • 3
    点赞
  • 踩
  • 1
    收藏
    觉得还不错? 一键收藏
  • 打赏
    打赏
  • 0
    评论
专栏目录
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

程序员小浩

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值