5 AOE网&关键路径

图论 —— AOE 网与关键路径_aoe缩短工期-CSDN博客

【数据结构】AOE网——关键路径_aoe网的关键路径-CSDN博客

语雀版本

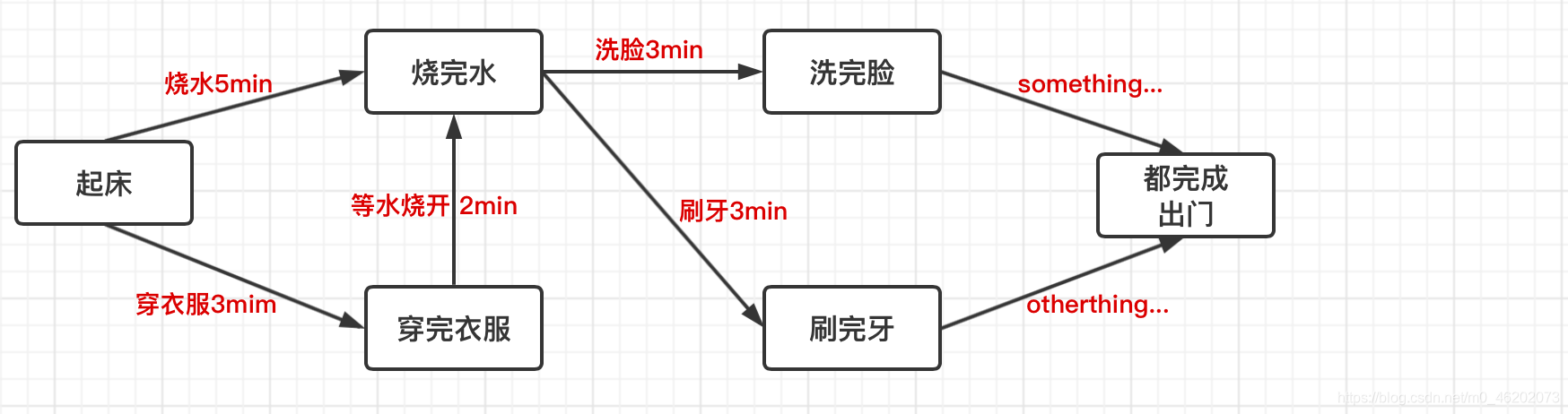
1 概念

**AOE网**： Activity On Edge Network，边表示活动的网。边是活动，顶点是事件（活动完成）。边带权，表示活动完成需要的时间。

源点：入度为0的点。

汇点：出度为0的点。

关键路径：从源点到汇点的最长路径。该路径的时间是整个工程完成的时间。

关键活动：关键路径上的活动。这些活动制约了工程的工期。

2 关键路径算法

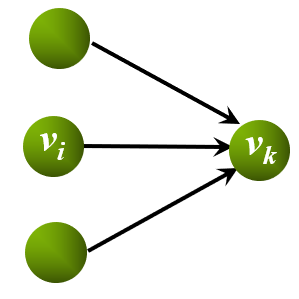
**事件的最早发生时间：**某个点k的ve(k)等于其前驱点加对应边权的最大值。表示该事件发生的最早时间。

ve(源点)=0

ve(k) = max{ve(i)+cost(i,k)}

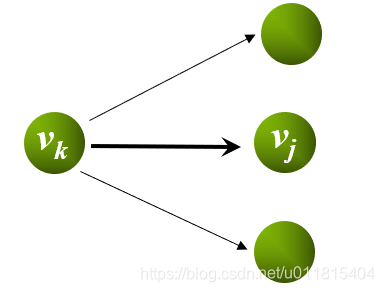
事件的最晚发生时间：某个点k的vl(k)等于其后继点-对应边权的最小值，表示在不影响工期的前提下该事件发生的最晚时间。

vl(汇点) = ve(汇点)

vl(k) = min{vl(j) - cost(k, j)}

活动的最早发生时间：某条边i的最早发生事件为起点的事件的最早发生时间。

活动为(k, j)，则 e(i) = ve(k)

活动的最晚发生时间：某条边i的最早发生事件为终点的事件的最迟发生时间减该边i的时间。

活动为(k, j)，则 l(i) = vl(j) - cost(k, j)

3 **代码**

3.1 **关键路径**

从源点求事件的最早发生时间ve->从汇点求事件的最晚发生时间vl->求活动的最早发生时间e->求活动的最晚发生时间l->找出e=l的边即为关键路径。

int n,m;
int G[N][N];//邻接矩阵
int in[N];//入度
int ve[N];//事件vk的最早发生时间
int vl[N];//事件vk的最晚发生时间
int ee[N];//活动ai的最早开始时间
int el[N];//活动ai的最晚开始时间
int Stack[N];//栈
struct Edge {
    int x,y;
    int dis;
    Edge(){}
    Edge(int x,int y,int dis):x(x),y(y),dis(dis){}
}edge[N];
bool vis[N];
 
void getVe(){//求ve
    int cnt=0;
    for(int i=1;i<=n;i++){
        int k=-1;
        for(int j=1;j<=n;j++){
            if(in[j]==0){
                Stack[++cnt]=j;
                k=j;
                in[j]=-1;
                break;
            }
        }
        for(int j=1;j<=n;j++){
            if(G[k][j]!=INF){
                ve[j]=max(ve[j],ve[k]+G[k][j]);
                in[j]--;
            }
        }
    }
}
void getVl(){//求vl
    memset(vl,INF,sizeof(vl));
    vl[Stack[n]]=ve[Stack[n]];
    for(int i=n;i>=1;i--){
        for(int j=1;j<=n;j++){
            if(G[Stack[i]][j]!=INF) {
                vl[Stack[i]]=min(vl[j]-G[Stack[i]][j],vl[Stack[i]]);
            }
        }
    }
}
void getEe(){//求ee
    for(int i=1;i<=m;i++)
        ee[i]=ve[edge[i].x];
}
void getEl(){//求el
    for(int i=1;i<=m;i++)
        el[i]=vl[edge[i].y]-edge[i].dis;
}
 
void printEdge(){//以边输出
    for(int i=1;i<=m;i++)
        if(ee[i]==el[i])
            printf("<%d,%d>:%d\n", edge[i].x, edge[i].y, edge[i].dis);
}
void printNode(){//以点输出
    priority_queue<int,vector<int>,greater<int> > Q;
    memset(vis,false,sizeof(vis));
    for(int i=1;i<=m;i++){
        if(ee[i]==el[i]){
            int x=edge[i].x;
            int y=edge[i].y;
            if(!vis[x]){
                Q.push(x);
                vis[x]=true;
            }
            if(!vis[y]){
                Q.push(y);
                vis[y]=true;
            }
        }
    }
    while(!Q.empty()){
        int temp=Q.top();
        Q.pop();
        printf("v%d ",temp);
    }
}
int main() {
    memset(G,INF,sizeof(G));
 
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
        int x,y,dis;
        scanf("%d%d%d",&x,&y,&dis);
        edge[i].x=x;
        edge[i].y=y;
        edge[i].dis=dis;
 
        G[x][y]=dis;
        in[y]++;
    }
 
    getVe();
    getVl();
    getEe();
    getEl();
 
    printf("以边输出：\n");
    printEdge();
    printf("以点输出：\n");
    printNode();
 
    return 0;
}

3.2 关键路径的长度

实际上求出ve，然后找打汇点的ve值就可以了

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

// 关键路径算法
int criticalPath(int n, vector<vector<int>>& edges) {
    // 邻接表表示图
    vector<vector<pair<int, int>>> graph(n);
    // 入度数组
    vector<int> inDegree(n, 0);
    // 最长路径数组
    vector<int> dist(n, 0);
    
    // 建立图
    for (const auto& edge : edges) {
        int u = edge[0], v = edge[1], w = edge[2];
        graph[u].emplace_back(v, w);
        inDegree[v]++;
    }
    
    // 拓扑排序队列
    queue<int> q;
    // 将入度为0的节点加入队列
    for (int i = 0; i < n; ++i) {
        if (inDegree[i] == 0) {
            q.push(i);
        }
    }
    
    // 拓扑排序并计算最长路径
    while (!q.empty()) {
        int node = q.front();
        q.pop();
        
        for (const auto& neighbor : graph[node]) {
            int v = neighbor.first;
            int weight = neighbor.second;
            // 更新最长路径
            dist[v] = max(dist[v], dist[node] + weight);
            // 入度减1
            inDegree[v]--;
            // 如果入度为0，加入队列
            if (inDegree[v] == 0) {
                q.push(v);
            }
        }
    }
    
    // 找到最长路径的长度
    return *max_element(dist.begin(), dist.end());
}

int main() {
    // 示例输入：节点数量和边
    int n = 6;
    vector<vector<int>> edges = {
        {0, 1, 3}, {0, 2, 2}, {1, 3, 2}, {2, 3, 4},
        {3, 4, 2}, {3, 5, 3}, {4, 5, 1}
    };
    
    int result = criticalPath(n, edges);
    cout << "关键路径的长度为: " << result << endl;
    return 0;
}