机器学习第九章----聚类

1、聚类任务

在“无监督学习”中，训练样本的标记信息是为未知的，目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律，为进一步的数据分析提供基础。常见的无监督学习任务有密度估计、异常检测，其中，研究最多，应用最广的是"聚类"。
聚类试图将数据集中的样本划分为若干个不相交的子集，每个子集称为一个簇。通过这样的划分，每个簇可能对应于一些潜在的概念，需说
聚类既能作为一个单独过程，用于寻找数据内存在的分布结构，也可作为分类等其他学习任务的前驱过程，例如，在一些商业应用中需对新用户的类型进行判别，但定义“用户类型”对商家来说却可能不太容易，此时往往可先对用户数据进行聚类，根据聚类结果将每个簇定义为一类，然后再基于这些类训练分类模型，用于判别新用户的类型。
基于不同的学习策略，人们设计出多种类型的聚类算法，再学习算法之前，去哦们五年先来了解一下聚类算法涉及的两个基本问题----性能度量和距离计算。

2、性能度量

聚类性能度量亦称聚类“有效性指标”，与监督学习中的性能度量作用相似，对聚类结果，我们需要通过某种性能度量来评估其好坏，另一方面，若明确了最终将要使用的性能度量，则可直接将其作为聚类过程的优化目标，从而更好地得到符合要求的聚类结果。
聚类是将样本集D划分为若干个互不相交的子集，即样本簇，那么，什么样的聚类结果比较好呢？直观上看，我们希望同一簇的样本尽可能彼此相似，不同簇的样本尽可能不同。换言之，聚类结果的“簇内相似度”高且“簇间相似度”低。
聚类性能度量有两类，一类是将聚类结果与某个“参考模型”进行比较，称为“外部指标”；另一类是直接考察聚类结果而不利用任何参考模型，称为“内部指标”。

对数据集$D=${$x_1,x_2,\dots \dots ,x_m$}，假定通过聚类给出的簇划分为 $C=${$C_1,C_2,\dots \dots ,C_k$}，参考模型给出的簇划分为 $C^{\ast }=${$C_1^{\ast },C_2^{\ast },\dots \dots ,C_k^{\ast }$}。相应地，令 $\lambda$与 ${\lambda }^{\ast }$分别表示$C$与$C^{\ast }$的簇标记向量。令$a$表示在$C$中属于相同簇在$c^{\ast }$中也属于相同簇的样本对的数目，$b$表示在$C$中属于相同簇在$c^{\ast }$中属于不同簇的样本对的数目，$c$表示在$C$中属于不同簇在$c^{\ast }$中属于相同簇的样本对的数目，$d$表示在$C$中属于不同簇在$c^{\ast }$中属于不同簇的样本对的数目

$\bullet$ Jaccard系数
$$JC=\frac{a}{a+b+c}$$
$\bullet$ FM指数
$$FMI=\sqrt{\frac{a}{a+b}\ast \frac{a}{a+c}}$$
$\bullet$ Rand指数
$$RI=\frac{2(a+d)}{m(m-1)}$$
显然，上述性能度量的结果值均在[0，1]区间，值越大越好。考虑聚类结果的簇划分$C=${$C_1,C_2,\dots \dots ,C_k$},定义$$\begin{gathered} avg(C)=\frac{2}{|C|(|C|-1)}\sum _{1\le i<j\le |C|}dist(x_i,x_j) \\ diam(C)=ma{x}_{1\le i<j\le |C|}dist(x_i,x_j) \\ {d}_{min}(C_i,C_j)=mi{n}_{x_i\in C_i,x_j\in C_j}dist(x_i,x_j) \\ {d}_{cen}(C_i,C_j)=dist({\mu }_i,{\mu }_j) \end{gathered}$$
其中，$\mu$代表的是簇C的中心点$\mu =\frac{1}{|C|}{\sum }_{1\le i\le |C|}{x}_i$，可知$avg(C)$对应的是簇c内样本间的平均距离，$diam(c)$对应的是簇C内样本间的最远距离，$d_{min}$对应的是簇$C_i$与簇$C_j$最近样本间的距离，$d_{cen}$对应的是簇$C_i$与簇$C_j$中心点间的距离。
基于上述各式可推导出以下常用的性能度量内部指标：

$\bullet$ DB指数(简称DBI)
$$DBI=\frac{1}{k}\sum _{i=1}^k\underset{j\ne 1}{\max }\left(\frac{avg(C_i)+avg(C_j)}{d_{cen}({\mu }_i,{\mu }_j)}\right)$$
$\bullet$ Dunn指数（简称DI）
$$DI=\underset{1\le i\le k}{\min }(\underset{j\ne i}{\min }(\frac{d_{min}(C_i,C_j)}{ma{x}_{1\le l\le k}diam(C_l)}))$$我们希望簇内样本距离尽可能小，簇间距离尽可能大，显然，DBI的值越小越好，而DI则相反，值越大越好。

3、距离计算

当函数$dist(.,.)$是一个距离度量时，需要满足以下基本性质：$$非负性：dist(x_i,x_j)\ge 0$$$$同一性:dist(x_i,x_j)=0,当且仅当x_i=x_j$$$$对称性：dist(x_i,x_j)=dist(x_j,x_i)$$$$直递性：dist(x_i,x_j)\le dist(x_i,x_k)+dist(x_k,x_j)$$
给定样本$x_i=(x_{i1},x_{i2},\dots \dots ,x_{in}),x_j=(x_{j1},x_{j2},\dots \dots ,x_{jn})$,它的“闵可夫斯基距离”定义为:$$dis{t}_{mk}(x_i,x_j)=(\sum _{u=1}^n|x_{iu}-x_{ju}{|}^p{)}^{\frac{1}{p}}$$当p=2时，闵可夫斯基距离即为欧式距离$$dis{t}_{ed}(x_i,x_j)=||x_i-x_j|{|}_2=\sqrt{\sum _{u=1}^n|x_{iu}-x_{ju}{|}^2}$$p=1时，闵可夫斯基距离即为曼哈顿距离$$dis{t}_{man}(x_i,x_j)=||x_i-x_j|{|}_1=\sum _{u=1}^n|x_{iu}-x_{ju}|$$我们常将属性划分为“连续属性”和“离散属性”。然而，在计算距离时，更为重要的是属性上是否定义了“序”关系。例如定义域为{1，2，3}的离散属性，我们可以直接在属性值上计算距离：1与2比较近，与3比较远,这样的属性称为有序属性；对不能直接在属性值上计算距离的离散属性，称为无序属性，比如颜色这个属性，假设有{红，黄，蓝}，我们不能简单的转化为{1，2，3}，因为原先的属性间没有明显的大小远近等“序”的关系。
对无序属性，可采用VDM(Value Difference Metric)距离，假设在属性$u$上取值为$a$的样本的个数为$m_{u,a}$,第$i$个样本簇中在属性$u$上取值为$a$的样本的个数为$m_{u,a,i}$，样本簇数为$k$，则属性$u$上的两个离散值$a$与$b$之间的VDM距离为$$VD{M}_p(a,b)=\sum _{i=1}^k|\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}{|}^p$$
将闵可夫距离和VDM距离混合可处理混合属性，假设有$n_c$个有序属性，$n-n_c$个无序属性，则$$MinkovD{M}_p(x_i,x_j)=(\sum _{u=1}^{n_c}|x_{iu}-x_{ju}{|}^p+\sum _{u=n_c+1}^{n}VD{M}_p(x_{iu},x_{ju}))$$
当样本空间中不同属性的重要性不同时，可使用“加权距离”。比如加权闵可夫距离,设属性的权重为$w_i$,($w_i>0,{\sum }_{i=1}^n{w}_i=1$)：$$dis{t}_{wmk}(x_i,x_j)=(w_1\ast |x_{i1}-x_{j1}{|}^p+\dots \dots +w_n|x_{in}-x_{jn}{|}^p{)}^{\frac{1}{p}}$$
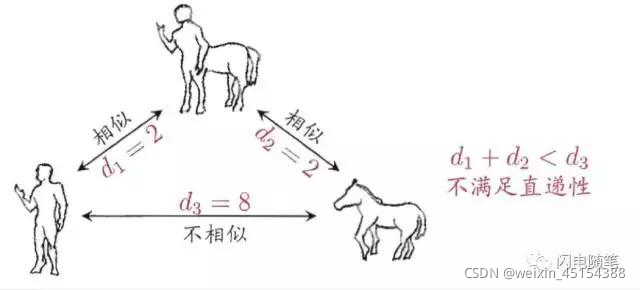
要注意的是，通常我们是基于某种形式的距离来定义"相似度度量"，距离越大，相似度越小。然而，用于相似度度量的距离未必一定要满足距离度量的所有基本性质。比如“人”、“马”都与“人马”比较相似，距离比较小，但人和马是不相似的，距离很大。此时该距离不再满足直递性，这样的距离称为“非度量距离”。

4、原型聚类

原型聚类亦称“基于原型的聚类“， 此类算法假设聚类结构能够通过一组原型刻画，在现实聚类任务中极为常用。通常情况下，算法先对原型进行初始化，然后对原型进行迭代更新求解。采用不同的原型表示，不同的求解方法，将产生不同的算法。下面介绍几种著名的原型聚类算法。

4.1 k均值算法

给定样本集$D=${$x_1,x_2，\dots \dots ，x_m$},“k均值”算法针对聚类所得簇划分$C=${$C_1,C_2,\dots \dots ,C_k$}，假设${\mu }_i$是簇$c_i$的均值向量，${\mu }_i=\frac{1}{C_i}{\sum }_{x\in C_i}x$，则它的平方误差为$$E=\sum _{i=1}^k\sum _{x\in C_i}||x-{\mu }_i|{|}_2^2$$
它刻画了簇内样本围绕簇均值向量的紧密程度，E值越小簇内样本相似度越高，因此，我们要想办法将上式最小化，为将其最小化，我们需要考察样本集D所有可能的簇划分。因此，k均值算法采用了贪心策略，通过迭代优化来近似求解上式。具体流程如下：

首先确定聚类簇数k，随机选择k个样本作为初始均值向量，计算样本$x_j$与均值向量之间的距离，将样本$x_j$划入相应的簇中，类似地，将数据集中所有样本划分到对应的簇，计算新划分后的簇的均值向量，更新均值向量后，不断重复上述过程，直至迭代产生的结果与上一轮形同，算法停止，得到最终的簇划分。

4.2 学习向量量化

与k均值算法类似，“学习向量量化(LVQ)”也是试图找出一组原型向量来刻画聚类结构，但与一般聚类算法不同的是，LVQ假设数据样本带有类别标记，在学习过程中利用样本的这些监督信息来辅助聚类。
给定样本集$D=${$(x_1,y_1),(x_2,y_2),\dots \dots ,(x_m,y_m)$},每个样本$x_j$是由n个属性描述的特征向量$(x_{j1};x_{j2};\dots \dots ,x_{jn})$,$y_j\in y$是样本$x_j$的类别标记。LVQ的目标是学得一组n维原型向量{$p_1,p_2,\dots \dots ,p_q$},每个原型向量代表一个聚类簇，簇标记 $t_i\in y$。
LVQ算法的具体过程如下图：

首先对原型向量进行初始化，假设有k个簇，第i个簇可从类别标记为$t_i$的样本中随机选取一个作为它的原型向量。随机选取一个具有标记的训练样本$x_j$，找出与其距离最近的原型向量$p_i^{\ast }$，若两者的类别标记相同，则更新原型向量为$$p^{{}^{\prime }}=p_i^{\ast }+\eta \ast (x_j-p_i^{\ast })$$更新后原型向量与样本之间的距离变为$$||p^{{}^{\prime }}-x_j|{|}_2=(1-\eta )\ast ||p_i^{\ast }-x_j|{|}_2$$可以发现，只要学习率$\eta \in (0,1)$,那么更新后原型向量就会更接近样本；当原型向量与样本的标记不同时更新原型向量为$$p^{{}^{\prime }}=p_i^{\ast }-\eta \ast (x_j-p_i^{\ast })$$使原型向量远离样本，不断重复上述过程直到满足停止条件（原型向量更新很小或达到最大迭代次数），将结果返回。学得原型向量后即可对样本进行划分，将它划入距离最近的原型向量所代表的簇中，我们的任务就完成了。

4.3 高斯混合聚类

数据分布由k个高斯成分混合而成，与k均值，LVQ用原型向量来刻画聚类结构不同，高斯混合聚类采用概率模型来表达聚类原型。对n维样本空间中的随机向量$x$,若$x$服从高斯分布，其概率密度函数为$$p(x)=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\sum {|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}(x-\mu {)}^T{\sum }^{-1}(x-\mu )}$$其中$\mu$是n维均值向量，$\sum$是$n\ast n$的协方差矩阵。可以看出，高斯分布由均值向量$\mu$和协方差矩阵$\sum$这两个参数确定。
将上式记为 $p(x|\mu ,\sum )$,则高斯混合分布可定义为$$p_M(x)=\sum _{i=1}^k{\alpha }_i\ast p(x|{\mu }_i,\sum _i)$$
可以看出，上式有k个成分，每个成分对应一个高斯分布。
假设样本的生成过程由高斯混合分布给出：首先，根据 ${\alpha }_1,{\alpha }_2,\dots \dots ,{\alpha }_k$定义的先验分布选择高斯混合成分，其中${\alpha }_i$为选择第i个混合成分的概率；然后，根据被选择的混合成分的概率密度函数进行采样，从而生成相应的样本。若训练集D={$x_1,x_2,\dots \dots ,x_m$}由上述过程生成，令随机变量$z_j\in${$1,2,\dots \dots ,k$}表示生成样本$x_j$的高斯混合成分，其取值未知。显然，$z_j$的先验概率$p(z_j=i)={\alpha }_i$,后验概率$$P_M(z_j=i|x_j)=\frac{P(z_j=i)\ast P_M(x_j|z_j=i)}{P_M(x_j)}=\frac{{\alpha }_i\ast P(x_j|{\mu }_i,{\sum }_i)}{\sum _{l=1}^k{\alpha }_l\ast p(x_j|{\mu }_l,{\sum }_l)}$$$P_M(z_j=i|x_j)$给出了样本$x_j$由第i个高斯混合成分生成的后验概率，记为${\gamma }_{ji}$,当高斯混合分布已知时，高斯混合聚类将把样本集D划分为k个簇$C=${$C_1,C_2,\dots \dots ,C_k$},每个样本$x_j$的簇标记${\lambda }_j$如下确定：$${\lambda }_j=\underset{i\in (1,2,\dots \dots ,k)}{\mathrm{argmax}}{\gamma }_{ji}$$因此，从原型聚类的角度来看，高斯混合聚类是采用概率模型对原型进行刻画，簇划分则由原型对应后验概率确定。
模型参数${\alpha }_i、{\mu }_i、{\sum }_i$可以通过极大似然法来确定，给定样本集D，它的d对数似然估计可写为$$LL(D)=ln(\prod _{j=1}^m{P}_m(x_j))=\sum _{j=1}^{m}ln(\sum _{i=1}^k{\alpha }_i\ast p(x_j|{\mu }_i,\sum _i))$$常用EM算法来对参数进行求解，将上式对${\mu }_i$求偏导为零，则$$\sum _{j=1}^m\frac{{\alpha }_i\ast p(x_j|{\mu }_i,{\sum }_i)}{{\sum }_{l=1}^k{\alpha }_l\ast p(x_j|{\mu }_l,{\sum }_l)}(x_j-{\mu }_i)=\sum _{j=1}^m{\gamma }_{ji}(x_j-{\mu }_i)=0$$由上式可得出$${\mu }_i=\frac{\sum _{j=1}^m{\gamma }_{ji}{x}_i}{\sum _{j=1}^m{\gamma }_{ji}}$$类似地，令$LL(D)$对${\sum }_i$求偏导为令可得$$\sum _i=\frac{\sum _{j=1}^m{\gamma }_{ji}(x_j-{\mu }_i)(x_j-{\mu }_i{)}^T}{\sum _{j=1}^m{\gamma }_{ji}}$$要想确定${\alpha }_i$的值，除了最大化，还要满足${\alpha }_i\ge 0,{\sum }_{i=1}^k{\alpha }_i=0$。用拉格朗日法对其求解，令$LL(D)+\lambda ({\sum }_{i=1}^k{\alpha }_i-1)$对${\alpha }_i$求偏导为零,得$$\sum _{j=1}^m\frac{p(x_j|{\mu }_i,{\sum }_i)}{{\sum }_{l=1}^k{\alpha }_l\ast p(x_j|{\mu }_l,{\sum }_l)}+\lambda =0$$两边同乘${\alpha }_i$,对所有有样本求和可得$\lambda =-m$，有$$\sum _{j=1}^m{\gamma }_{ji}+\lambda {\alpha }_i=0$$因此，$${\alpha }_i=\frac{1}{m}\sum _{j=1}^m{\gamma }_{ji}$$
高斯混合聚类算法的过程如下：

先确定混合而成分的个数，初始化混合分布的模型参数，基于ENM算法不断对模型参数进行迭代更新直到满足停止条件，根据确定的高斯混合分布进行簇划分后返回最终结果。

5、密度聚类

密度聚类亦称“基于密度的聚类”，此类算法假设聚类结构能通过样本分布的紧密程度确定。通常情形下，密度聚类算法从样本密度的角度来考察样本之间的可能性，并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。
DBSCAN是一种著名的密度聚类算法，它基于一组"邻域"参数来刻画样本分布的紧密程度。给定数据集$D=${$x_1,x_2,\dots \dots ,x_m$},定义下面几个概念：

$\bullet$ $ϵ$-邻域 ：对于样本$x_j\in D$,与样本之间的距离小于等于$ϵ$的样本的集合称为它的$ϵ$-邻域 N ϵ = { x i ∈ D ∣ d i s t ( x i , x j ) ≤ ϵ } N_\epsilon = \{x_i \in D | dist(x_i,x_j) \leq \epsilon\} Nϵ​={xi​∈D∣dist(xi​,xj​)≤ϵ}。
$\bullet$ 核心对象：若$x_j$的$ϵ$-邻域包含的样本数超过$MinPts$个,则$x_j$是一个核心对象。
$\bullet$ 密度直达：若$x_j$位于$x_i$的$ϵ$-邻域中，且$x_i$是核心对象，则称$x_j$由$x_i$密度直达。
$\bullet$ 密度可达：对$x_i$与$x_j$，若存在样本序列$p_1,p_2,\dots \dots ,p_n$,其中$p_1=x_i,p_n=x_j$且$p_{i+1}$由$p_i$密度直达，则称$x_j$由$x_i$密度可达。
$\bullet$ 密度相连：对$x_i$与$x_j$，若存在$x_k$使得$x_i$与$x_j$均由$x_k$密度可达，则称$z_i$与$x_j$密度相连。

基于这些概念，DBSCAN将簇定义为：由密度可达关系导出的最大的密度相连样本集合。给定邻域参数，簇 $C\subseteq D$是满足以下性质的非空样本子集：
$$\begin{gathered} 连接性：x_i\in C,x_j\in C\Rightarrow x_i与x_j密度相连 \\ 最大性：x_i\in C,x_j由x_i密度可达\Rightarrow x_j\in C \end{gathered}$$
那么，如何从数据集D中找出满足以上性质的聚类簇呢？实际上，若x为核心对象，由x密度可达的所有样本组成的结合记为 $X=${$x^{{}^{\prime }}\in D|x^{{}^{\prime }}由x密度可达$}，则不难证明X即为满足连接性与最大性的簇。
DBSCAN先任选数据集中的一个核心对象为“种子”，在由此出发确定相应的聚类簇。具体过程如下：
先根据给定的邻域参数$(ϵ,MinPts)$找出所有核心对象,确定核心对象集$\Omega$,然后随机选取一个核心对象找出由它密度可达的所有样本，这样我们就构成了第一个聚类簇。然后将聚类簇中包含的核心对象从$\Omega$中去掉，再从更新后的$\Omega$中随机选取种子来生成下一个聚类簇。上述过程不断重复，直到$\Omega$为空。

6、层次聚类

层次聚类试图在不同层次对数据集进行划分， 从而形成树形的聚类结构。数据集的划分可采用“自底向上”的聚合策略，也可采用“自顶向下”的分拆策略。
AGNES是一种采用自底向上聚合策略的层次聚类算法，它先将数据集中的每一个样本看作一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并，该过程不断重复，直至达到预设的聚类簇个数。关键在于如何计算聚类簇之间的距离，实际上，每个簇是一个样本集合，因此，只需采用关于集合的某种距离即可。例如，给定聚类簇$c_i$和$c_j$，可通过下面的式子来计算距离：
$$\begin{gathered} 最小距离：d_{min}=(C_i,C_j)=\underset{x\in C_i,z\in C_j}{\min }dist(x,z) \\ 最大距离：d_{max}(C_i,C_j)=\underset{x\in C_i,z\in C_j}{\max }dist(x,z) \\ 平均距离：d_{avg}(C_i,C_j)=\frac{1}{|C_i||C_j|}\sum _{x\in C_i}\sum _{z\in C_j}dist(x,z) \end{gathered}$$
显然，最小距离由两个簇的最近样本决定，最大距离由两个簇的最远样本决定，而平均距离则由两个簇的所有样本共同决定。当聚类簇距离由$d_{min}、d_{max}、d_{avg}$计算时，AGNES算法相应地被称为"单链接"、“全连接”、或“均链接”算法
AGNES算法的具体流程如下：

先对仅含一个样本的初始聚类簇和相应的距离矩阵进行初始化，然后不断合并距离最近的聚类簇并对合并得到的聚类簇的距离矩阵进行更新，不断重复，直至达到预设的聚类簇数。