OpenCV-Python (官方)中文教程(部分一)_Day15

一诺加油鸭

于 2025-04-23 16:32:29 发布

阅读量797

点赞数 33

分类专栏： python+人工智能文章标签： opencv python 人工智能

本文链接：https://blog.csdn.net/weixin_45420601/article/details/147457307

版权

python+人工智能专栏收录该内容

16 篇文章

订阅专栏

18.图像梯度

梯度简单来说就是求导。

OpenCV 提供了三种不同的梯度滤波器,或者说高通滤波器：Sobel, Scharr和Laplacian。Sobel,Scharr 其实就是求一阶或二阶导数。Scharr 是对 Sobel（使用小的卷积核求解求解梯度角度时）的优化。Laplacian 是求二阶导数。

Sobel算子和Scharr算子

1. Sobel 算子

原理

Sobel 算子结合了高斯平滑和微分操作，能有效抑制噪声。

它计算图像的一阶梯度（导数），分为水平方向（x方向）和垂直方向（y方向）：

x方向：检测垂直边缘（对水平变化敏感）。

y方向：检测水平边缘（对垂直变化敏感）。

卷积核

3×3 Sobel 核（x方向）：

3×3 Sobel 核（y方向）：

特点

抗噪声能力强（因高斯平滑）。

可通过 ksize 参数调整核大小（如 3×3、5×5）。

2. Scharr 算子

原理

Scharr 是 Sobel 的改进版，对边缘的响应更强，尤其在3×3核时效果更优。

当 ksize=-1 时，OpenCV 会自动使用 Scharr 核替代 Sobel。

卷积核

3×3 Scharr 核（x方向）：

3×3 Scharr 核（y方向）：

特点

比 Sobel 的梯度计算更精确，适合对边缘敏感的场景。

计算速度与 Sobel 相同，推荐在 3×3 核时优先使用。

Sobel 算子是高斯平滑与微分操作的结合体,所以它的抗噪声能力很好。你可以设定求导的方向（xorder 或 yorder）。还可以设定使用的卷积核的大小（ksize）。如果 ksize=-1,使用 3x3 的 Scharr 滤波器要比 3x3 的 Sobel 滤波器的效果好（而且速度相同,所以在使用 3x3 滤波器时应该尽量使用 Scharr 滤波器）。3x3 的 Scharr 滤波器卷积核如下：

3.Laplacian算子

原理

Laplacian 算子是二阶导数算子，直接计算图像的曲率（即梯度的梯度），能同时突出边缘和角点。

它对噪声敏感，通常需先高斯滤波（如结合 GaussianBlur）。

卷积核

3×3 Laplacian 核：

扩展核（增强对角线响应）：

特点

直接检测灰度突变区域（如边缘、孤立点）。

OpenCV 内部通过调用 Sobel 算子实现二阶导数计算。

拉普拉斯(Laplacian)算子可以使用二阶导数的形式定义,可假设其离散实现类似于二阶 Sobel 导数,事实上,OpenCV 在计算拉普拉斯算子时直接调用 Sobel 算子。计算公式如下：

拉普拉斯滤波器使用的卷积核：

三者的对比

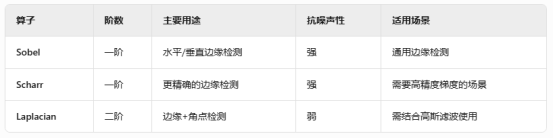
关键点总结

Sobel/Scharr：一阶导数，检测边缘方向；Scharr 在 3×3 核时更优。

Laplacian：二阶导数，对噪声敏感，需配合平滑使用。

卷积核：不同核决定了算子的敏感性和计算特性。

import cv2

import numpy as np

# 读取图像（灰度化）

img = cv2.imread('2.png', cv2.IMREAD_GRAYSCALE)

# Sobel 算子

#cv2.CV_64F：输出图像的深度（64位浮点型，避免梯度计算时的截断）。1, 0：对 x 方向求一阶导数（检测垂直边缘）。

#0, 1：对 y 方向求一阶导数（检测水平边缘）。ksize=3：使用 3×3 的 Sobel 核

sobel_x = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=3) #检测垂直边缘x方向

#Sobel/Laplacian 的输出是浮点数，直接显示可能导致全白/全黑

sobel_x = cv2.convertScaleAbs(sobel_x) # 转为8位无符号整型

sobel_y = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=3) #检测水平边缘y方向

# Scharr 算子（当 ksize=-1 时自动启用）更精确的边缘检测

scharr_x = cv2.Scharr(img, cv2.CV_64F, 1, 0)

#Sobel/Laplacian 的输出是浮点数，直接显示可能导致全白/全黑

scharr_x = cv2.convertScaleAbs(scharr_x)

scharr_y = cv2.Scharr(img, cv2.CV_64F, 0, 1)

# Laplacian 算子计算图像的二阶导数，同时突出边缘和角点（如纹理细节）。对噪声敏感，通常需先高斯滤波（但代码中未预处理）。

laplacian = cv2.Laplacian(img, cv2.CV_64F)

#二阶导数可能产生负值，需取绝对值

laplacian = np.absolute(laplacian) # 取绝对值

laplacian = np.uint8(255 * laplacian / np.max(laplacian)) # 归一化

# 水平拼接三个结果

combined = np.hstack((sobel_x, scharr_x, laplacian))

# 显示合并后的图像

cv2.imshow('Sobel X | Scharr X | Laplacian', combined)

cv2.waitKey(0)

cv2.destroyAllWindows()

结果：

总结

Sobel：检测方向性边缘（分x/y方向）。

Scharr：更精确的3×3边缘检测。

Laplacian：检测边缘+角点（二阶导数）。

应用场景：

车牌识别（Sobel找边缘）

医学图像分析（Scharr增强细节）

纹理分析（Laplacian突出特征）

代码

下面的代码分别使用以上三种滤波器对同一幅图进行操作。使用的卷积核都是5x5。

import cv2

from matplotlib import pyplot as plt

img=cv2.imread('dave.jpg',0)

#cv2.CV_64F 输出图像的深度（数据类型），可以使用-1, 与原图像保持一致 np.uint8

laplacian=cv2.Laplacian(img,cv2.CV_64F)

# 参数 1,0 为只在 x 方向求一阶导数，最大可以求 2 阶导数。

sobelx=cv2.Sobel(img,cv2.CV_64F,1,0,ksize=5) # 参数 0,1 为只在 y 方向求一阶导数，最大可以求 2 阶导数。

sobely=cv2.Sobel(img,cv2.CV_64F,0,1,ksize=5)

plt.subplot(2,2,1),plt.imshow(img,cmap = 'gray')

plt.title('Original'), plt.xticks([]), plt.yticks([])

plt.subplot(2,2,2),plt.imshow(laplacian,cmap = 'gray')

plt.title('Laplacian'), plt.xticks([]), plt.yticks([])

plt.subplot(2,2,3),plt.imshow(sobelx,cmap = 'gray')

plt.title('Sobel X'), plt.xticks([]), plt.yticks([])

plt.subplot(2,2,4),plt.imshow(sobely,cmap = 'gray')

plt.title('Sobel Y'), plt.xticks([]), plt.yticks([])

plt.show()

结果：

注意!

在查看上面这个例子的注释时不知道你有没有注意到：当我们可以通过参数 -1 来设定输出图像的深度（数据类型）与原图像保持一致,但是我们在代码中使用的却是 cv2.CV_64F。这是为什么呢？想象一下一个从黑到白的边界的导数是整数,而一个从白到黑的边界点导数却是负数。如果原图像的深度是 np.int8 时,所有的负值都会被截断变成 0,换句话说就是把边界丢失掉。

所以如果这两种边界你都想检测到,最好的的办法就是将输出的数据类型设置的更高,比如 cv2.CV_16S,cv2.CV_64F 等。取绝对值然后再把它转回到cv2.CV_8U。

1. 为什么不能直接用 cv2.CV_8U（8位无符号整数）？

问题场景：

假设图像中有一个从白→黑的边缘（如下图），其导数（梯度值）为负值。

白像素(255) → 黑像素(0) → 导数 = 0 - 255 = -255

数据类型的影响：

如果输出深度是 cv2.CV_8U（0~255的无符号整数），所有负值会被截断为0。

结果：白→黑的边缘完全丢失，只能检测黑→白的边缘！

2. 为什么用 cv2.CV_64F（64位浮点数）？

关键原因：

保留负值：导数计算结果可能是正（黑→白）、负（白→黑）或零（平坦区域）。

浮点类型（如 CV_64F）可以存储这些负数，避免截断。

后续处理：

通过 np.absolute() 或 cv2.convertScaleAbs() 取绝对值，再转回 cv2.CV_8U 显示。

3. 不同数据类型的对比示例

(1) 错误做法：直接输出 cv2.CV_8U

laplacian_bad = cv2.Laplacian(img, cv2.CV_8U) # 负值被截断为0

cv2.imshow('Bad (CV_8U)', laplacian_bad) # 丢失白→黑边缘

效果：边缘不完整，部分方向消失。

(2) 正确做法：使用 cv2.CV_64F + 取绝对值

laplacian_good = cv2.Laplacian(img, cv2.CV_64F) # 保留负值

laplacian_good = np.absolute(laplacian_good) # 取绝对值

laplacian_good = np.uint8(laplacian_good) # 转回8位显示

cv2.imshow('Good (CV_64F)', laplacian_good) # 完整边缘

效果：所有方向的边缘均被检测到。

4. 数据类型选择建议

5. 完整流程的代码注释

import cv2

import numpy as np

# 读取图像（灰度化）

img = cv2.imread('image.jpg', cv2.IMREAD_GRAYSCALE)

# Step 1: 使用 cv2.CV_64F 保留负值导数

laplacian = cv2.Laplacian(img, cv2.CV_64F) # 输出包含正/负/零

# Step 2: 取绝对值（白→黑和黑→白边缘均保留）

laplacian_abs = np.absolute(laplacian)

# Step 3: 归一化到 0~255 并转为 8位无符号整型

laplacian_8u = np.uint8(255 * laplacian_abs / np.max(laplacian_abs))

# 显示结果

cv2.imshow('Laplacian Edges', laplacian_8u)

cv2.waitKey(0)

cv2.destroyAllWindows()

结果：

import cv2

import numpy as np

def enhanced_laplacian_edge_detection(image_path, blur_ksize=(5,5), display=True):

    """优化的Laplacian边缘检测函数



    Args:

        image_path: 输入图像路径

        blur_ksize: 高斯模糊核大小，默认(5,5)

        display: 是否显示结果，默认True



    Returns:

        处理后的边缘图像

    """

    # 1. 图像读取与预处理

    img = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

    if img is None:

        raise FileNotFoundError(f"无法加载图像: {image_path}")



    # 2. 高斯模糊降噪（优化：自动计算sigma）

    blurred = cv2.GaussianBlur(img, blur_ksize, sigmaX=0)



    # 3. Laplacian边缘检测（优化：使用CV_16S节省内存）

    laplacian = cv2.Laplacian(blurred, cv2.CV_16S, ksize=3)



    # 4. 后处理（优化：自适应对比度增强）

    laplacian_abs = cv2.convertScaleAbs(laplacian) # 比np.absolute更快



    # 自适应归一化（排除前5%的极值）

    v_min, v_max = np.percentile(laplacian_abs, [5, 95])

    laplacian_norm = np.clip((laplacian_abs - v_min) * 255. / (v_max - v_min), 0, 255)

    laplacian_8u = laplacian_norm.astype(np.uint8)



    # 5. 可选显示

    if display:

        # 对比显示原图与结果

        comparison = np.hstack([img, laplacian_8u])

        cv2.imshow(f'Original vs Enhanced Laplacian (ksize={blur_ksize})', comparison)

        cv2.waitKey(0)

        cv2.destroyAllWindows()



    return laplacian_8u

# 使用示例

enhanced_edges = enhanced_laplacian_edge_detection('2.png', blur_ksize=(7,7))