你也能懂的微积分（一）

微积分有多重要相信大家多多少少心里都有点数，搞数学的不会微积分就跟中学生不

会“加减乘除”一样，基本上啥都干不了。牛顿是物理学界的封神人物，然而牛顿还凭借

着微积分的发明，跟阿基米德、高斯并称为世界三大数学家，这是何等荣耀？这又从侧

面反映出微积分是何等地位？

除了重要，很多人对微积分的另一个印象就是难。在许多人眼里，微积分就是高深数学

的代名词，就是高智商的代名词，许多家长一听说谁家孩子初中就学了微积分，立马就

感叹这是别人家的天才。其实不然，微积分并不难，它的基本思想甚至是非常简单的，

不然也不会有那么多初中生学习微积分的事了。

所以，大家在看这篇文章的时候不要有什么心理负担，微积分并不是什么很难的东西，

我们连高大上的麦克斯韦方程组都看过来了，还怕什么微积分对不对？只要跟着长尾科技的思路走，我相信一般的中学生都是可以非常顺畅地理解微积分的。

好，下面进入正题。

01从面积说起

我们从小学就学了各种求面积的公式，什么长方形、三角形、圆、梯形等等，然后“求

阴影部分的面积”就成了小时候的一块心理阴影。

不知道大家当时有没有想过一个问题：好像我们每学一种新图形就有一个新的面积公

式，可是，世界上有无数种图形啊，难道我要记无数种公式么？这太令人沮丧了！

更令人沮丧的是，还有很多图形根本就没有什么面积公式。比如我随手在纸上画一条曲

线，这条曲线围成的面积你要用什么公式来算？但是，它确实围成了一块确定大小的区

域啊，大小是确定的就应该能算出面积来，算不出来就是你的数学不行，对吧？于是，

这个事就深深地刺痛了数学家们高傲的内心，然后就有很多人来琢磨这个事，比如阿基

米德。

如何求一条曲线围成的面积？

面对这个问题，古今中外的数学家的想法都是类似的，那就是：用我们熟悉的图形（比

如三角形、长方形等）去逼近曲线围成图形的面积。这就好比在铺地板砖的时候，我们

会用尽可能多的瓷砖去填满地板，然后这些瓷砖的面积之和差不多就是地板的面积。

阿基米德首先考虑抛物线：如何求抛物线和一条直线围成的面积？抛物线，顾名思义，

就是你往天上抛一块石头，这块石头在空中划过的轨迹。如下图的外层曲线：

这条抛物线和直线BC围成了一个弓形（形状像一把弓箭，涂了颜色的部分），这个弓

形的面积要怎么求呢？阿基米德的想法是用无数个三角形去逼近这个弓形，就好像我们

用很多三角形的瓷砖去铺满这块弓形的地板一样。

他先画了一个蓝色的大三角形ABC（这个三角形并不是随意画的，抛物线在A点处的切

线必须跟BC平行。这里我们不细究，只要知道能够画出这样一个三角形就行）。当然，这个三角形ABC的面积肯定比弓形的面积小，小多少呢？显而易见，小了左右两边

两个小弓形的面积。

如果我们能把这两个小弓形的面积求出来，加上三角形ABC就可以求出原来大弓形的面

积了。但是，如何求这两个小弓形的面积呢？答案是：继续用三角形去逼近！

于是，阿基米德又使用同样的方法，在这两个小弓形里画了两个绿色的三角形。同样

的，在这两个小弓形被两个绿色三角形填充之后，我们又多出了四个弓形，然后我们又

用四个黄色的三角形去填充剩余的弓形……

很显然，这个过程可以无限重复下去。我们可以用1个蓝色，2个绿色的，4个黄色的，

8个红色的等无穷多个三角形来逼近这个弓形。我们也能很直观地感觉到：我们使用的

三角形越多，这些三角形的面积之和就越接近大弓形的面积。用三角形的面积之和来逼

近这个弓形面积，这我没意见，但关键是你要怎样求这么多三角形（甚至是无穷多个三

角形）的面积呢？

这就是阿基米德厉害的地方，他发现：每次新画的三角形的面积都是上一轮三角形面积

的1/4。也就是说，2个绿色三角形的面积之和刚好是1个蓝色三角形面积的1/4；4个

黄色的三角形的面积之和刚好是2个绿色三角形的1/4，那么就是1个蓝色三角形面积的

1/16，也就是（1/4）²……

如果我们把所有三角形的面积都折算成第一个蓝色三角形ABC（用△ABC表示）的面

积，那么大弓形的面积S就可以这样表示：

S=△ABC+（1/4）△ABC+（1/4）²△ABC +（1/4）³△ABC……

这东西放在今天就是一个简单的无穷级数求和问题，但阿基米德是古希腊人，那是秦始

皇都还没统一中国的年代，什么高等数学更是不存在的，怎么办呢？阿基米德计算了几项，直觉告诉他这个结果在不断地逼近（4/3）△ABC，也就是说你

用的三角形越多，面积S就越接近（4/3）△ABC。于是阿基米德就猜测：如果我把无穷

多个三角形的面积都加起来，这个结果应该刚好等于（4/3）△ABC。

当然，光猜测是不行的，数学需要的是严格的证明，然后阿基米德就给出了证明。他证

明如果面积S大于（4/3）△ABC会出现矛盾，再证明如果它小于（4/3）△ABC也会出

现矛盾，所以这个面积S就只能等于（4/3）△ABC，证毕。

就这样，阿基米德就严格地求出了抛物线和直线围成的弓形的面积等于△ABC的4/3，

他使用的这种方法被称为“穷竭法”。

02一千年以后

时光荏苒，再见已经是一千八百年后的十七世纪了。

穷竭法可以精确地算出一些曲线围成的面积，但是它有个问题：穷竭法对于不同曲线围

成的面积使用不同的图形去逼近。比如上面使用的是三角形，在其它地方就可能使用其

它图形，不同图形证明技巧就会不一样，这样就比较麻烦。

到了十七世纪，大家就统一使用矩形（长方形）来做逼近：不管你是什么曲线围成的图

形，我都用无数个矩形来逼近你，而且都沿着x轴来做切割。这样操作上就简单多了。

还是以抛物线为例，这次我们考虑 简单的抛物线y=x²，它的图像大概就是下面这样

（每取一个x的值，y的值都是它的平方），我们来具体算一算这条抛物线在0到1之间

与x轴围成的面积是多少。

我们用矩形来逼近原图形，容易想象，矩形的数量越多，这些矩形的面积之和就越接近

曲线围成的面积。这个思路跟穷竭法类似，但是更容易理解。

我们假设0到1之间被平均分成了n份，那么每一份的宽度就是1/n。而矩形的高度就是

函数的纵坐标的值，纵坐标可以通过y=x²很容易算出来。于是，我们就知道，第1个矩

形的高度为（1/n）²，第2个为（2/n）²，第3个为（3/n）²……

有了宽和高，把它们乘起来就是矩形的面积。于是，所有矩形的面积之和S就可以写成

这样：

这只是一段普通的化简，相信大家只要知道平方和公式是下面这样就秒懂了：

于是，我们就得到了n个矩形面积之和的表达式：

因为n是矩形的个数，n越大，矩形的数量就越多，那么这些矩形的面积之和就越接近

曲线围成的面积。所以，如果n变成了无穷大，我们从“直觉”上认为，这些矩形的面积

之和就应该等于抛物线围成的面积。

与此同时，如果n是无穷大，那么这个表达式的后两项1/2n和1/6n²从直觉上来看就应

该无限趋近于0，或者说等于无穷小，似乎也可以扔掉了。

于是，当n趋向于无穷大的时候，面积S就只剩下第一项1/3。所以，我们就把抛物线

y=x²与x轴在0到1之间围成的面积S算出来了，结果不多不少，就等于1/3。

看完这种计算方法，大家有什么想说的？觉得它更简单，更神奇了，或者其它什么的？

大家注意一下我的措辞，在这一段里我用一些诸如“直觉上”、“应该”、“似乎”这种不是很精确的表述。在大家的印象里，数学应该最精确、最严密的一门学科啊，怎么能用这

些模糊不清的词来形容呢？

03严密性和实用性

然而，这正是问题所在：不是我不想讲清楚，而是在这个时候根本就讲不清楚。别说我

讲不清楚，牛顿和莱布尼茨也讲不清楚，这跟阿基米德用穷竭法求面积时的那种精确形

成了鲜明的对比。

使用穷竭法求面积，比如为了得到4/3△ABC，阿基米德就去证明如果它大于4/3会出

现矛盾，小于4/3也会出现矛盾，所以你就必须等于4/3。这是非常严密的，虽然操作

上麻烦了点，但是逻辑上无懈可击。

但是到了17世纪，我们是怎么得到抛物线与x轴围成的面积等于1/3的呢？我们得到了n

个矩形的面积公式：

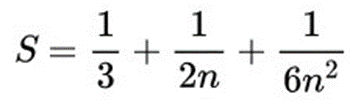
然后，我们觉得当n越来越大的时候，后面两项1/2n和1/6n²的值会越来越小，当n变

成无穷大的时候，后面两项应该就是无穷小。于是，我们就认为可以把它直接舍弃了，

所以面积S就只剩下第一项1/3。但问题是，无穷小是多小？从直觉上来看，不论n取多大，1/2n和1/6n²都应该是大于

0的，我们可以直接把0舍掉，但是对于并不等于0的数我们能直接舍弃掉么？这样做的

合法性依据在哪里？

相对于古希腊的穷竭法，17世纪这种“统一用矩形来逼近原图形”的想法简单了不少，但

同时也失去了一些精确性。虽然它计算的结果是正确的，但是它的逻辑并不严密。逻辑

不严密的话，你拿什么保证你今天这样用是正确的，明天我那样用它还是正确的？

想想数学为什么这么令人着迷，为什么《几何原本》至今都保持着无与伦比的魅力？不

就是因为数学的血液里一直流淌着无可挑剔的逻辑严密性么？

古希腊人或许早就知道17世纪这种更简单的计算方法，但是因为方法不够严密，所以

他们压根不屑于使用。他们宁可绕弯使用更麻烦，但是在逻辑上无懈可击的穷竭法，因

为对他们而言：逻辑的严密性，远比计算结果的实用性重要。

在对严密性和实用性的取舍上，东西方走了截然不同的两条路：古代中国毫不犹豫地选

择了实用性。他们需要数学帮助国家计算税收，计算桥梁房屋等建筑工程，计算商业活

动里的各种经济问题。所以，代表中国古代数学的《九章算术》，里面全是教你怎么巧

妙地计算这个计算那个。也因此，古代中国会有那么多能工巧匠，会有那么多设计精巧

的建筑工程。

西方则截然相反，古希腊人坚定不移的选择了严密性。他们需要严密的逻辑帮他们认识

世界的本原，认识世界是由什么组成的，为什么世界会是现在这个样子。所以，代表西

方古代数学的《几何原本》就是教你怎么从5个显而易见的公理出发，通过严密的逻辑

一步步推导出400多个多定理，即便这些定理并不显而易见。因此，西方能诞生现代科

学。

失去简单性，数学会失去很多；失去严密性，数学将失去一切。至于如何让它变得严

密，后面我们再细说。

待续。。。