MATLAB-6-2线性方程组求解

1. 线性方程组的直接解法

1）高斯（Guass）消去法、列主元消去法、矩阵的三角分解法

经典的直接法，由其改进得到的列主元消去法是目前计算机上求解线性方程组的标准算法。列主元消去法通过消元将一般线性方程组的求解问题转化为三角方程组的求解问题。

2）利用左除运算符：使用列主元消去法

Ax=b， x=A\b（b左除以A）
若矩阵A是奇异或接近奇异，则MATLAB会给出警告信息。
e.g.用左除运算符求解下列线性方程组

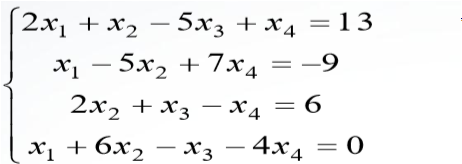
>> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
>> b=[13;-9;6;0];
>> x=A\b
x =
  -66.5556
   25.6667
  -18.7778
   26.5556
%求逆方法需要更多的计算量，所以不建议用矩阵的求逆方法；求逆方法可能给出不精确的解。

3）矩阵分解

将一个给定的矩阵分解成若干个特殊类型矩阵的乘积，从而将一个一般的矩阵计算问题转化为几个易求的特殊矩阵的计算问题。优点：运算速度快，节省存储空间
可分为LU分解、QR分解、Cholesky分解

i. LU分解（lower and upper）

将一个n阶矩阵表示为一个下三角矩阵和一个上三角矩阵的乘积。只要方阵是非奇异的，LU分解总成立。

ii. MATLAB的LU分解函数

LU分解函数根据列主元LU分解算法定义，具有较好的数据稳定性。
LU函数调用格式：

• [L,U]=lu(A)：产生一个上三角阵U和一个变换形式的下三角阵L，使之满足A=LU。
  矩阵A必须为方阵。这里的L不是通常意义上的下三角阵，但可以通过一个行交换成为一个下三角阵。
• [L,U,P]=lu(A)：产生一个上三角阵U、一个下三角阵L和一个置换矩阵P，使之满足PA=LU。矩阵A必须为方阵。

iii. 用LU分解求解线性方程组

Ax=b，LUx=b，x=U(L\b) 或 Ax=b，PAx=Pb，LUx=Pb，x=U(L\P*b)
%连续左除时，注意左除的顺序
e.g. 用LU分解求解上述e.g.中的线性方程组

>> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
>> b=[13,-9,6,0]';
%矩阵中用逗号分隔，所以需要转置
>> [L,U]=lu(A);
>> x=U\(L\b)
%添加括号保证优先级
x =
  -66.5556
   25.6667
  -18.7778
   26.5556
%结果相同
%也可以：
>> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
>> b=[13,-9,6,0]';
>> [L,U,P]=lu(A);
>> x=U\(L\P*b)
x =
  -66.5556
   25.6667
  -18.7778
   26.5556

2. 线性方程组的迭代解法

需要给定迭代的初始值，再逐步迭代到最优值

1）雅可比（Jacobi）迭代法

Ax=b，A为非奇异方阵，主对角线元素不等于0，A可分解为A=D-L-U
D为对角阵，L、U分别为下三角阵、上三角阵负数。
(D-L-U)x=b
Dx-(L+U)x=b
x=D⁻¹(L+U)x+D⁻¹b
与之对应的迭代公式为：
x^(k+1)=D⁻¹ (L+U) x^(k)+D⁻¹b
x^(k+1)=Bx^(k)+f
B和f固定不变

函数文件jacobi.m
function [y,n]=jacobi(A,b,x0,ep)
D=diag(diag(A));
%提取矩阵A主对角线元素，产生一个列向量；以diag(A)为主对角线元素，产生对角矩阵
L=-tril(A,-1);
%提取矩阵A第-1条主对角线及以下元素，取负
U=-triu(A,1);
%提取矩阵A第1条主对角线及以上元素，取负
B=D\(L+U);
f=D\b;
y=B*x0+f;
%x0为初始值，y为迭代后的值
n=1;
while norm(y-x0)>=ep
	x0=y;
	y=B*x0+f;
	n=n+1;
end
输入参数：系数矩阵，右端列向量，迭代初值，精度
输出参数：方程的解和迭代次数
终止条件：前后两次求得的解很接近时，结束迭代过程
解是否接近衡量：用前后两个解之差的2范数，判断两个解向量是否很接近

2）高斯-赛德尔（Gauss-Serdel）迭代法

雅可比（Jacobi）迭代法对已计算出的信息，未充分利用
Dx-(L+U)x=b
(D-L)x=Ux+b
x=(D−L)⁻¹Ux+(D−L)^-1b
与之对应的迭代公式
x^(k+1)=(D−L)⁻¹Ux^(k)+(D−L)⁻¹b
x^(k+1)=Bx^(k)+f

函数文件guaseidel.m
function [y,n]=gauseidel(A,b,x0,ep)
D=diag(diag(A));
L=-tril(A,-1);
U=-triu(A,1);
B=(D-L)\U;
f=(D-L)\b;
y=B*x0+f;
n=1;
while norm(y-x0)>=ep
	x0=y;
	y=B*x0+f;
	n=n+1;
end
%与jacobi.m函数文件类似，只是系数矩阵改变

e.g. 分别用雅可比迭代法和高斯-赛德尔迭代法求解线性方程组。设迭代初始值为0，迭代精度为10^(-6)。
首先创建jacobi.m和gauseidel.m函数文件。

>> A=[4,-2,-1;-2,4,3;-1,-3,3];
>> b=[1;5;0];
>> [x,n]=jacobi(A,b,[0;0;0],1.0e-6)
x =
    0.9706
    0.8529
    1.1765
n =
    35
>> [x,n]=gauseidel(A,b,[0;0;0],1.0e-6)
x =
    0.9706
    0.8529
    1.1765
n =
    16

e.g.分别用雅可比迭代法和高斯-赛德尔迭代法求解下列方程组，看是否收敛。

>> A=[1,2,-2;1,1,1;2,2,1];
>> b=[9;7;6];
>> [x,n]=jacobi(A,b,[0;0;0],1.0e-6)
x =
   -27
    26
     8
n =
     4
>> [x,n]=gauseidel(A,b,[0;0;0],1.0e-6)
x =
   NaN
   NaN
   NaN
n =
   1012

两种迭代方法的结果好坏，与具体方程组有关。

3. 总结

直接法：以矩阵初等变换为基础，可以求得方程组的精确解；占用的内存空间大、程序实现较为复杂；一般适合求解低阶稠密线性方程组。
迭代法：从给定初始值逐步逼近精确解的过程，求解过程占用存储空间小，程序设计简单；适用于求解大型稀疏矩阵线性方程组；要考虑算法的收敛性。