集合论与图论（下）

概念：

图

零图：只有点没有边的图；

重边：两个节点不只有一条边；

线图：没有重边；

简单图：没有重边，没有环；

子图：新生成的图的点和边是原来图点和边的子集，如果两个图不同就是真子图；

生成子图：新生成的图点的个数和原来的图点的个数相同，但是边比原来的边少；

导出子图：新生成的图的点的集合是原来图的点的集合的子集，包含了与点相连的所有边；

边导出子图：边集合是原来集合的子集，包含所有与边相连的点；

无向完全图边数：n*(n-1)/2;

有向完全图：kn=n*(n-1);

补图：从完全图中删除相应的边；

度数deg(v)：结点V关联的边数；（自环2次）

度数之和等于边数的2倍；

奇度顶点有偶数个；

简单无向图中，n个节点最多n-1度，如果有两个以上的n-1度结点则不可能有1度顶点；

同构：必要条件：1）结点数相同，2）边数相同，3）度数序列相同；

一个自补图必有4k或4k+1个结点；

通路：两个结点之间有路径；

通路长度：经过的边数；

回路：出发点和终点相同；

简单通路/回路：边不相同；

初级通路/回路：结点和边都不重复；

割点：删除此结点后就不连通；

割边：删除此边后就不连通；

最大度：G中最大度数；

最小度：G中最小度数；

点连通度：最少删去几个结点不连通；

边连通度：最少删去几个边就不连通；

强连通：任意两结点存在通路；

单向连通图：任意两结点至少有单向通路；

弱连通图（基图）：去掉方向是连通的；

k-正则图：在一个无向简单图之中，如果每个节点的度数均为K,则称该图为k-正则图。显然完全图kn是(n-1)正则图。

树

树中边数=结点数-1；

度数之和等于边数的二倍；

任意非平凡树至少有两片树叶；

F有k个连通分支，m条边的n阶森林，m=n-k；

树叶：出度为0；

内点：入度为1，出度大于等于1；

特殊图

欧拉图

欧拉回路：经过每条边1次且仅1次的回路；

无向图中所有节点的度数为偶数；

有向图中所有结点的入度=出度；

欧拉通路：无向图中只有0个或者2个奇度顶点；

有向图中：（1）入度等于出度，（2）除两个结点外，所有结点入度等于出度，一个出度比入度大1，一个入度比出度大1；

哈密顿图

哈密顿图或哈密顿回路：经过每个结点1次且仅1次的回路；（带有割点就不是哈密顿图）

哈密顿通路：存在经过每个节点1次且仅1次的通路；

判断哈密顿图充分条件：

1、对于顶点个数大于2的图，如果图中任意两点度的和大于或等于顶点总数，那这个图一定是哈密顿图。但不满足不一定就不是哈密顿图；

2.若图的最小度不小于顶点数的一半，则图是哈密顿图；

3.若图中每一对不相邻的顶点的度数之和不小于顶点数，则图是哈密顿图。不满足不一定就不是；

4.m=(n-1)*(n-2)/2+2则一定是哈密顿图

判断哈密顿图必要条件：

1. 删除k个节点，连通分支>k，则G必然不是哈密顿图

2. 可以用两种颜色染色并且染色后顶点数不相同必然不是哈密顿图

3. 有三个度数为1的顶点，则必然没有哈密顿路

由于用两种颜色染色后，1个结点数是8另一种颜色结点数是6所以不是哈密顿图

偶图（二部图）

图中所有回路长为偶数；

完全偶图km，n的边数是m*n，当m和n是偶数是，km,n是欧拉图；当m=n>1时，完全二部图是哈密顿图；

G是简单二部图，则m<=(n^2)/4

平面图

k5和k3，3是典型的非平面图，如果图中含有这两个图则一定不是平面图；

结论：

1. 平面图有n个结点，m个边，r个面，则n-m+r=2;

2. 若有k个连通分支，则n-m+r=k+1;

3. 所有面次数之和等于边数的2倍；

4. 若简单连通平面图有n（n大于等于3）个节点，m条边，则m<=3n-6;

5. 若简单连通平面图有n（n大于等于3）个节点，m条边，每个面都是由4条及以上的边构成则m<=2n-4;

6. 若简单连通平面图有n（n大于等于3）个节点，m条边，每个面都是由k条及以上的边构成则m<=k(n-2)/(k-2);

	欧拉图	哈密顿图	二部图	平面图
k2,3			1	1
k3,3		1	1
k4		1
k5	1	1
km,n	m,n是偶数	m=n>1	1	m<3或n<3
kn	n为奇	n不等于2	n=2	n<5

习题：

第一讲：

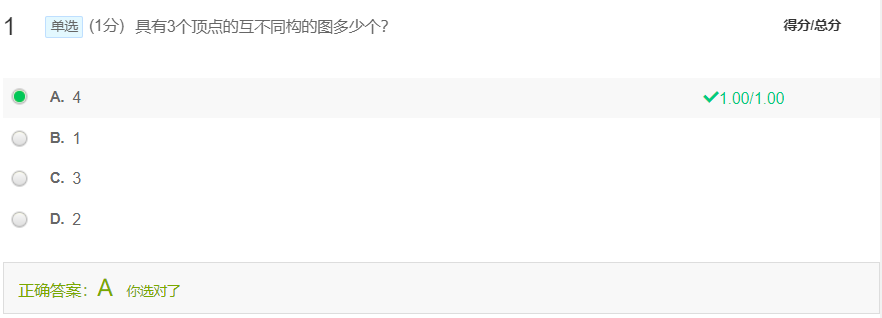
同构不光要顶点数，边数相同，还要有相同的度数序列；

奇度顶点有偶数个；

第二讲：

1. 3，1，1，1；

2. 2，2，1，1；

3. 2，2，2，2；

4. 3，2，2，1；

5. 3，3，2，2；

6. 3，3，3，3；

由于度数之和等于边数的二倍，所以任何图（非零图）的度数之和一定是偶数；

如果图是一条直线，那么边数=结点数-1；

如果是一个完全图那么就不含有顶点度数为1；

如果是自补图，顶点数只能是4k或者是4k+1；

n*(n-1)=132可以解出来n=12，让这12个点作为完全图，任加一个点就是非连通图；

作为拓展处理出了直接选；

画图，一摸一样就是自补图；

第三讲：

存在欧拉闭迹就是指存在欧拉回路或者是欧拉图，判断每个点是否是偶度，如果不是则不存在欧拉闭迹；

找出图中奇度顶点的个数，对他们除二向下取整就是需要几笔才能画出；

只有A有奇度顶点并且有4个，4/2=2所以需要两笔完成；

A是欧拉图，一笔就可以完成；

B不是欧拉图，有2个奇度顶点至少一笔完成；

C不是欧拉图有4个奇度顶点至少两笔完成；

D有6个奇度顶点至少要三笔完成；

k4每个顶点度数为3是奇数所以不含有欧拉闭迹；

推论：kn存在欧拉闭迹的充分条件是n是奇数；

每个顶点度数是5所以不含有欧拉闭迹；

k3,3有6个奇度顶点所以至少需要3笔画成；

欧拉开迹就是指存在欧拉通路，那么含有0个或2个奇度顶点的图就存在欧拉开迹

第四讲：哈密顿图

其余几个图删去4个结点连通分支大于4

A不存在哈密顿路有割点

二部图只有m=n>1才是哈密顿图

用染色法一种颜色结点个数是7另一种是9不相等

染色法

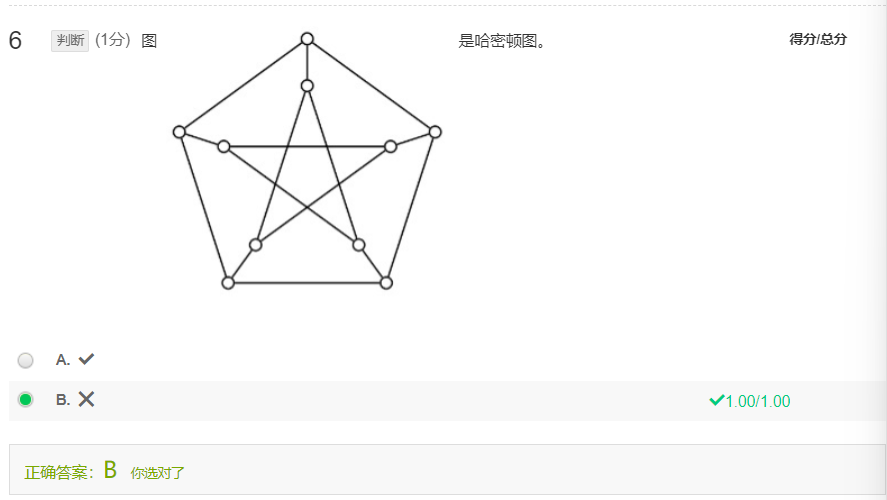
直观判断每经过一个节点则删去该节点，无法回到起始

5个顶点每个顶点度数为2的图是哈密顿图但不满足

第五讲：图的表示、带权图

第六讲：树、割集

2个结点的树

只有根节点的树

第七讲：图的连通度

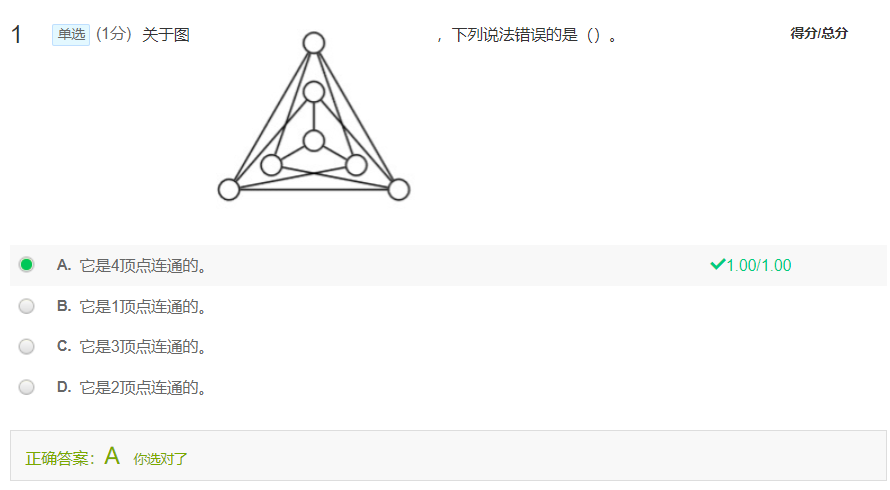
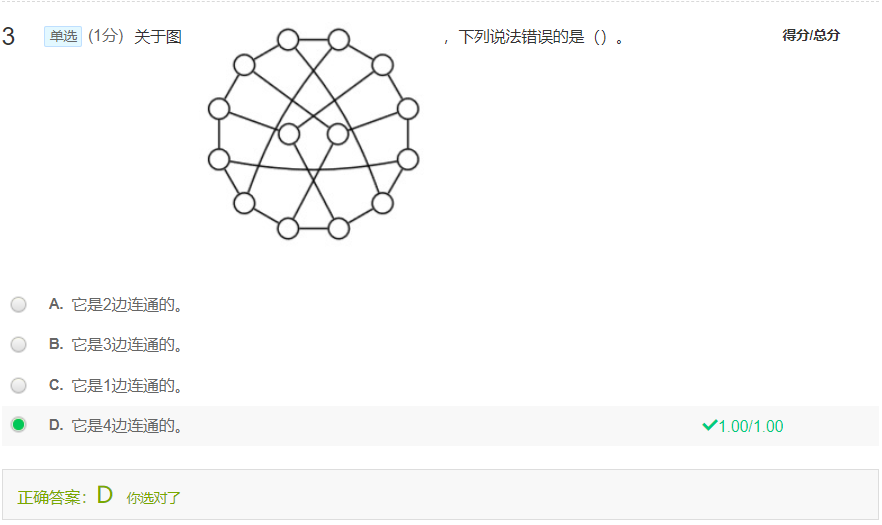
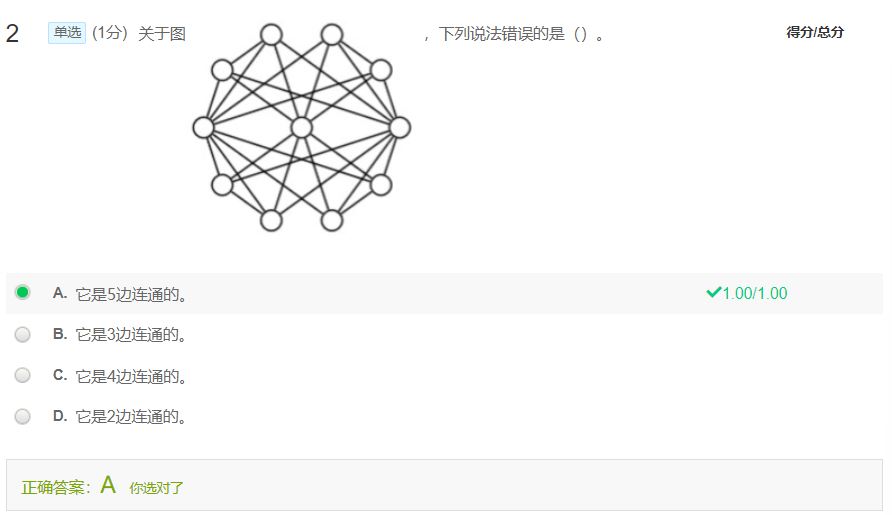
选最大的就完事了

第八讲：匹配问题

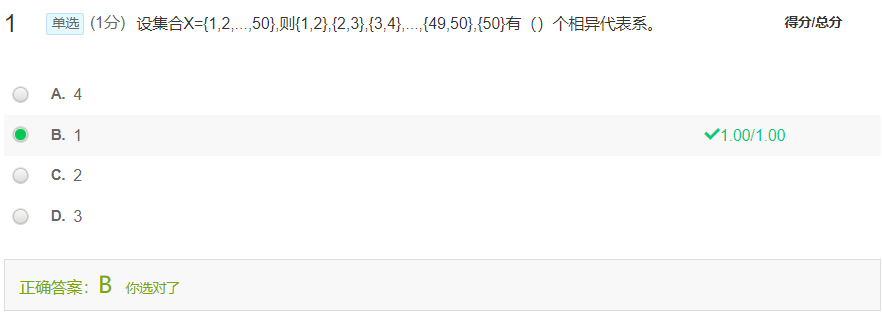
{1,2.....49,50}

有相异代表系就是在每个集合中选出一个元素，直到所有集合都能选出不同的元素

第九讲：平面图

第十讲：图的顶点着色问题

第十一讲：有向图的基本概念

应该选B答案有误

第十二讲：有根树、有序树、比赛图

二叉树左右结点形态不同