吴恩达深度学习笔记（二）——浅层神经网络

一、选择激活函数的经验法则

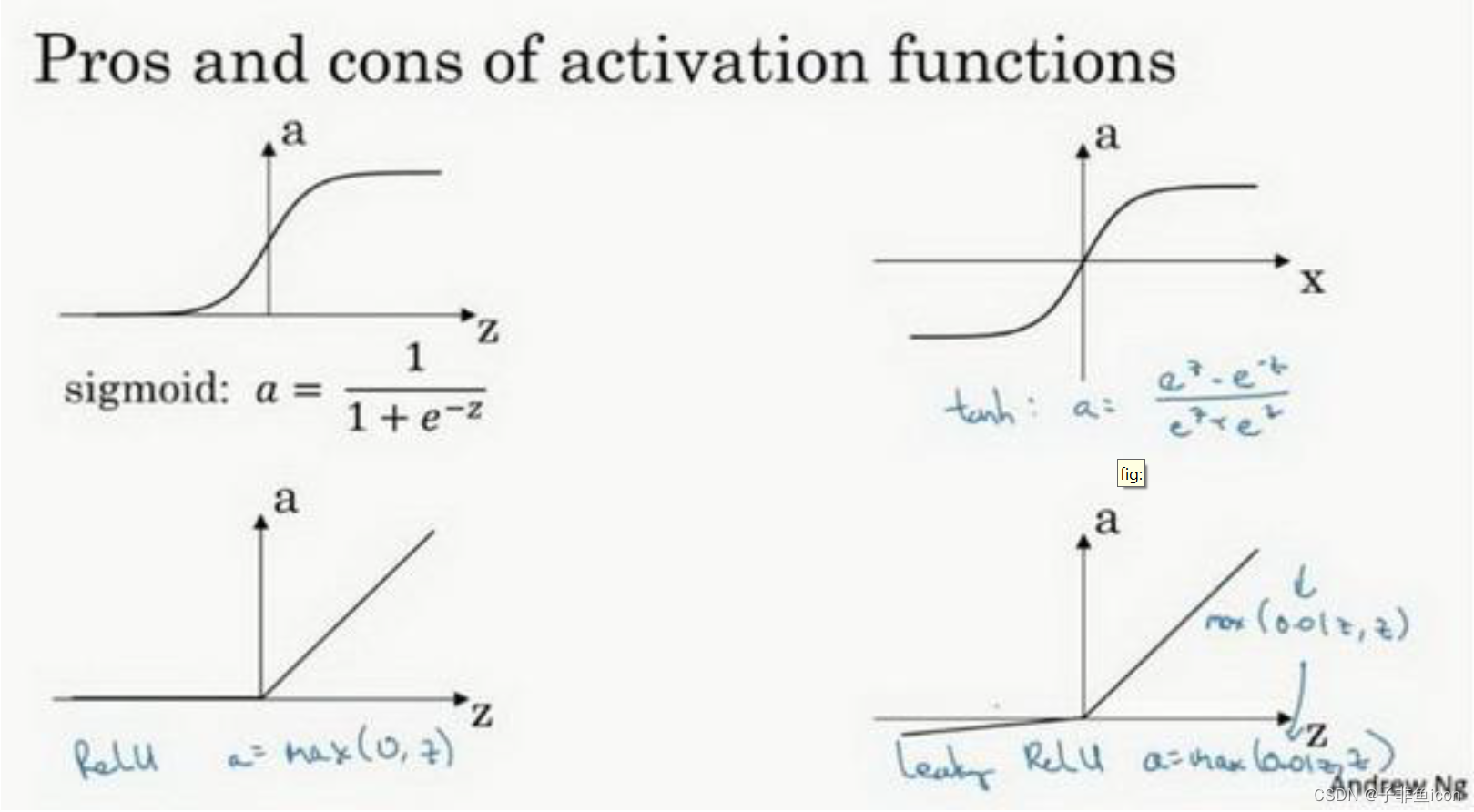
课后题：tanh激活函数通常比隐藏层单元的sigmoid激活函数效果更好，因为其输出的平均值更接近于零，因此它将数据集中在下一层是更好的选择，使得下一层的学习变得更加简单。

因为tanh具有更强的梯度：由于数据以0为中心，导数更高，且能避免梯度中的偏差。参考文章/参考PDF

二、需要线性激活函数的原因

只有一个地方可以使用线性激活函数------g(z)=z，就是你在做机器学习中的回归问题。 y是一个实数，举个例子，比如你想预测房地产价格，y 就不是二分类任务0或1，而是一个实数，从0到正无穷。如果y 是个实数，那么在输出层用线性激活函数也许可行，你的输出也是一个实数，从负无穷到正无穷。

总而言之，不能在隐藏层用线性激活函数，可以用ReLU或者tanh或者leaky ReLU或者其他的非线性激活函数，唯一可以用线性激活函数的通常就是输出层；除了这种情况，会在隐层用线性函数的，除了一些特殊情况，比如与压缩有关的，那方面在这里将不深入讨论。在这之外，在隐层使用线性激活函数非常少见。因为房价都是非负数，所以我们也可以在输出层使用ReLU函数这样你的y_hat都大于等于0。

三、随机初始化

对于逻辑回归，可以将权重初始化为0.但对于一个神经网络，如果把权重或者参数初始化为0，那么梯度下降将不会起到任何作用。

随机初始化的权重也不能太大！

四、编程作业

4.1 load_planar_dataset()函数

def load_planar_dataset():
    np.random.seed(1)
    m = 400 # number of examples  样本个数
    N = int(m/2) # number of points per class  每一个种类的个数
    D = 2 # dimensionality 维度
    X = np.zeros((m,D)) # data matrix where each row is a single example 每一行是一个样本
    Y = np.zeros((m,1), dtype='uint8') # labels vector (0 for red, 1 for blue) dtype=uint8的数据类型往往可以用作掩码，0表示舍弃对应项，1表示选取对应项
    a = 4 # maximum ray of the flower   花瓣的最大长度/半径
	# 这段代码相当于生成花瓣的x,y坐标，都存在X中，关于散点的颜色则存在Y中
    for j in range(2):  
        ix = range(N*j,N*(j+1))
        t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta 角度
        r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius  4决定了有8个花瓣
        X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]  # 左右拼接
        Y[ix] = j

    X = X.T
    Y = Y.T

    return X, Y

np.c_的用法

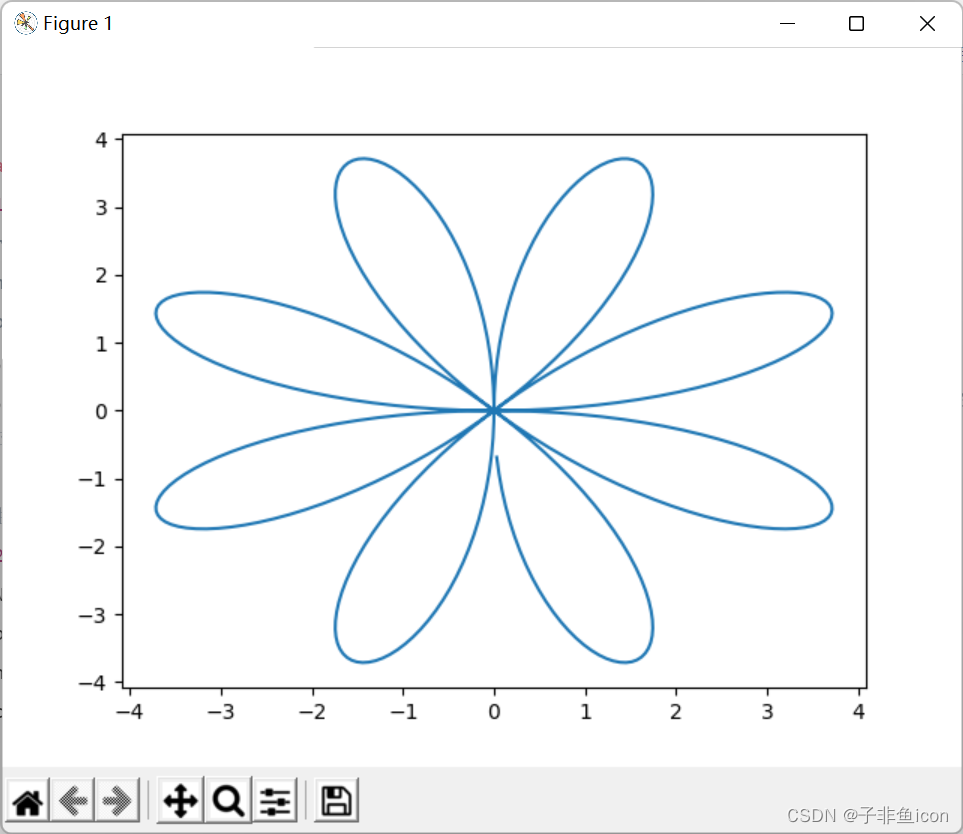
r = a*sin(4t): (此处屏蔽了噪声）

t = np.linspace(j*3.12,(j+1)*3.12,N) #+ np.random.randn(N)*0.2 # theta
r = a*np.sin(6*t)# + np.random.randn(N)*0.2 # radius
...
plt.plot(X[0,:],X[1,:])
plt.show()

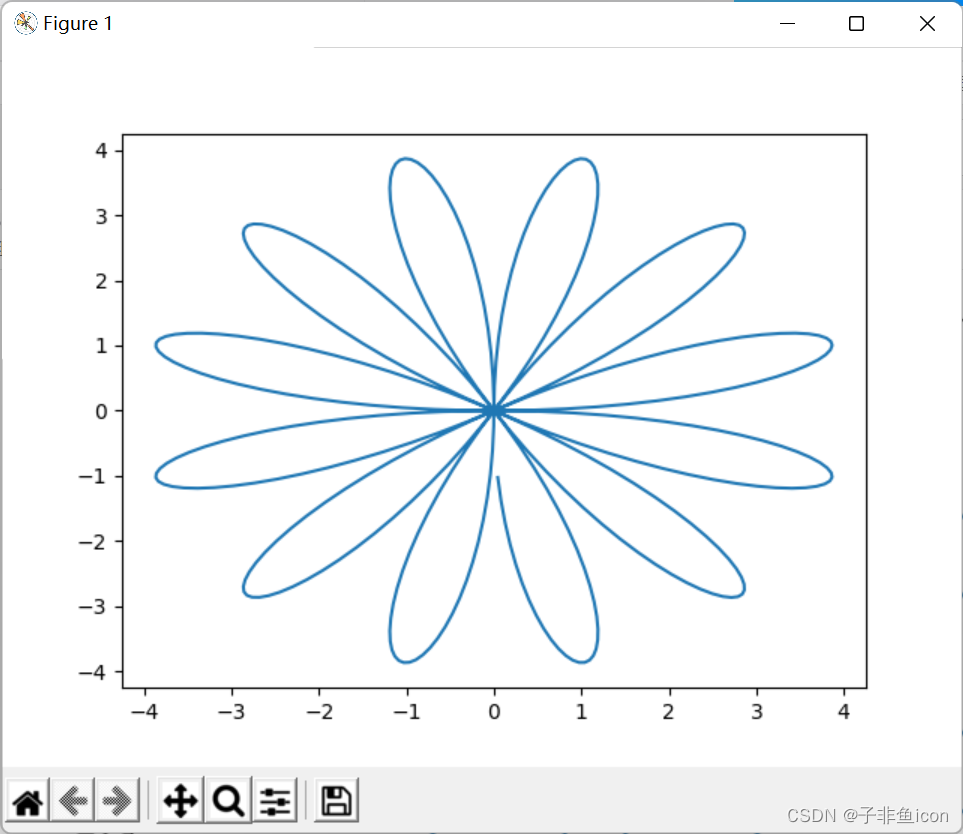
r = a*sin(6t):

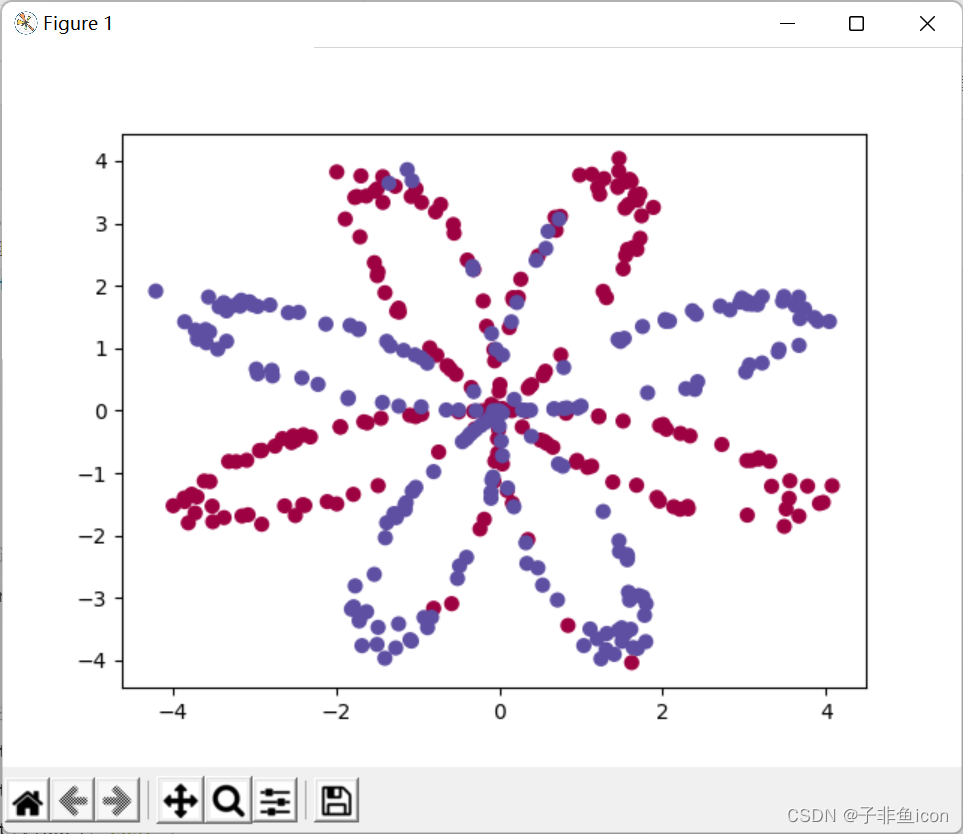
4.2 plt.scater()函数

plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral) #绘制散点图

s表示点的大小

cmap = plt.cm.Spectral实现的功能是给c=Y为1的点一种颜色，给label为0的点另一种颜色。

参考链接1

参考链接2

4.3 plot_decision_boundary(model, X, y)函数

参考链接

def plot_decision_boundary(model, X, y):
    # Set min and max values and give it some padding
    x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1  # 周围多增加一些面积
    y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))  # 绘制网格
    # Predict the function value for the whole grid
    Z = model(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral) # 画出分类的边界线
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)

plt.contourf()划分界线

参考链接

4.4 完整代码

参考链接1

参考链接2

planar_utils.py

import matplotlib.pyplot as plt
import numpy as np
import sklearn
import sklearn.datasets
import sklearn.linear_model

def plot_decision_boundary(model, X, y):
    # Set min and max values and give it some padding
    x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
    y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole grid
    Z = model(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)
    plt.show()


def sigmoid(x):
    s = 1/(1+np.exp(-x))
    return s

def load_planar_dataset():
    np.random.seed(1)
    m = 400 # number of examples
    N = int(m/2) # number of points per class
    D = 2 # dimensionality
    X = np.zeros((m,D)) # data matrix where each row is a single example
    Y = np.zeros((m,1), dtype='uint8') # labels vector (0 for red, 1 for blue)
    a = 4 # maximum ray of the flower

    for j in range(2):
        ix = range(N*j,N*(j+1))
        t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta
        r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius
        X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
        Y[ix] = j

    X = X.T
    Y = Y.T

    return X, Y

def load_extra_datasets():  
    N = 200
    noisy_circles = sklearn.datasets.make_circles(n_samples=N, factor=.5, noise=.3)
    noisy_moons = sklearn.datasets.make_moons(n_samples=N, noise=.2)
    blobs = sklearn.datasets.make_blobs(n_samples=N, random_state=5, n_features=2, centers=6)
    gaussian_quantiles = sklearn.datasets.make_gaussian_quantiles(mean=None, cov=0.5, n_samples=N, n_features=2, n_classes=2, shuffle=True, random_state=None)
    no_structure = np.random.rand(N, 2), np.random.rand(N, 2)

    return noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure

testCases.py

#-*- coding: UTF-8 -*-
"""
# WANGZHE12
"""
import numpy as np

def layer_sizes_test_case():
    np.random.seed(1)
    X_assess = np.random.randn(5, 3)
    Y_assess = np.random.randn(2, 3)
    return X_assess, Y_assess

def initialize_parameters_test_case():
    n_x, n_h, n_y = 2, 4, 1
    return n_x, n_h, n_y

def forward_propagation_test_case():
    np.random.seed(1)
    X_assess = np.random.randn(2, 3)

    parameters = {'W1': np.array([[-0.00416758, -0.00056267],
        [-0.02136196,  0.01640271],
        [-0.01793436, -0.00841747],
        [ 0.00502881, -0.01245288]]),
     'W2': np.array([[-0.01057952, -0.00909008,  0.00551454,  0.02292208]]),
     'b1': np.array([[ 0.],
        [ 0.],
        [ 0.],
        [ 0.]]),
     'b2': np.array([[ 0.]])}

    return X_assess, parameters

def compute_cost_test_case():
    np.random.seed(1)
    Y_assess = np.random.randn(1, 3)
    parameters = {'W1': np.array([[-0.00416758, -0.00056267],
        [-0.02136196,  0.01640271],
        [-0.01793436, -0.00841747],
        [ 0.00502881, -0.01245288]]),
     'W2': np.array([[-0.01057952, -0.00909008,  0.00551454,  0.02292208]]),
     'b1': np.array([[ 0.],
        [ 0.],
        [ 0.],
        [ 0.]]),
     'b2': np.array([[ 0.]])}

    a2 = (np.array([[ 0.5002307 ,  0.49985831,  0.50023963]]))

    return a2, Y_assess, parameters

def backward_propagation_test_case():
    np.random.seed(1)
    X_assess = np.random.randn(2, 3)
    Y_assess = np.random.randn(1, 3)
    parameters = {'W1': np.array([[-0.00416758, -0.00056267],
        [-0.02136196,  0.01640271],
        [-0.01793436, -0.00841747],
        [ 0.00502881, -0.01245288]]),
     'W2': np.array([[-0.01057952, -0.00909008,  0.00551454,  0.02292208]]),
     'b1': np.array([[ 0.],
        [ 0.],
        [ 0.],
        [ 0.]]),
     'b2': np.array([[ 0.]])}

    cache = {'A1': np.array([[-0.00616578,  0.0020626 ,  0.00349619],
         [-0.05225116,  0.02725659, -0.02646251],
         [-0.02009721,  0.0036869 ,  0.02883756],
         [ 0.02152675, -0.01385234,  0.02599885]]),
  'A2': np.array([[ 0.5002307 ,  0.49985831,  0.50023963]]),
  'Z1': np.array([[-0.00616586,  0.0020626 ,  0.0034962 ],
         [-0.05229879,  0.02726335, -0.02646869],
         [-0.02009991,  0.00368692,  0.02884556],
         [ 0.02153007, -0.01385322,  0.02600471]]),
  'Z2': np.array([[ 0.00092281, -0.00056678,  0.00095853]])}
    return parameters, cache, X_assess, Y_assess

def update_parameters_test_case():
    parameters = {'W1': np.array([[-0.00615039,  0.0169021 ],
        [-0.02311792,  0.03137121],
        [-0.0169217 , -0.01752545],
        [ 0.00935436, -0.05018221]]),
 'W2': np.array([[-0.0104319 , -0.04019007,  0.01607211,  0.04440255]]),
 'b1': np.array([[ -8.97523455e-07],
        [  8.15562092e-06],
        [  6.04810633e-07],
        [ -2.54560700e-06]]),
 'b2': np.array([[  9.14954378e-05]])}

    grads = {'dW1': np.array([[ 0.00023322, -0.00205423],
        [ 0.00082222, -0.00700776],
        [-0.00031831,  0.0028636 ],
        [-0.00092857,  0.00809933]]),
 'dW2': np.array([[ -1.75740039e-05,   3.70231337e-03,  -1.25683095e-03,
          -2.55715317e-03]]),
 'db1': np.array([[  1.05570087e-07],
        [ -3.81814487e-06],
        [ -1.90155145e-07],
        [  5.46467802e-07]]),
 'db2': np.array([[ -1.08923140e-05]])}
    return parameters, grads

def nn_model_test_case():
    np.random.seed(1)
    X_assess = np.random.randn(2, 3)
    Y_assess = np.random.randn(1, 3)
    return X_assess, Y_assess

def predict_test_case():
    np.random.seed(1)
    X_assess = np.random.randn(2, 3)
    parameters = {'W1': np.array([[-0.00615039,  0.0169021 ],
        [-0.02311792,  0.03137121],
        [-0.0169217 , -0.01752545],
        [ 0.00935436, -0.05018221]]),
     'W2': np.array([[-0.0104319 , -0.04019007,  0.01607211,  0.04440255]]),
     'b1': np.array([[ -8.97523455e-07],
        [  8.15562092e-06],
        [  6.04810633e-07],
        [ -2.54560700e-06]]),
     'b2': np.array([[  9.14954378e-05]])}
    return parameters, X_assess

L1W3.py

import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets


np.random.seed(1) # 设置一个固定的随机种子，以保证结果一致

# 加载和查看数据集
X, Y = load_planar_dataset() # 花的二类数据集
X_shape = X.shape
Y_shape = Y.shape
m = X.shape[1]  # 样本个数
print("X的维度：", X_shape)
print("Y的维度：", Y_shape)
print("样本个数：", m)

plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral) #绘制散点图
plt.show()

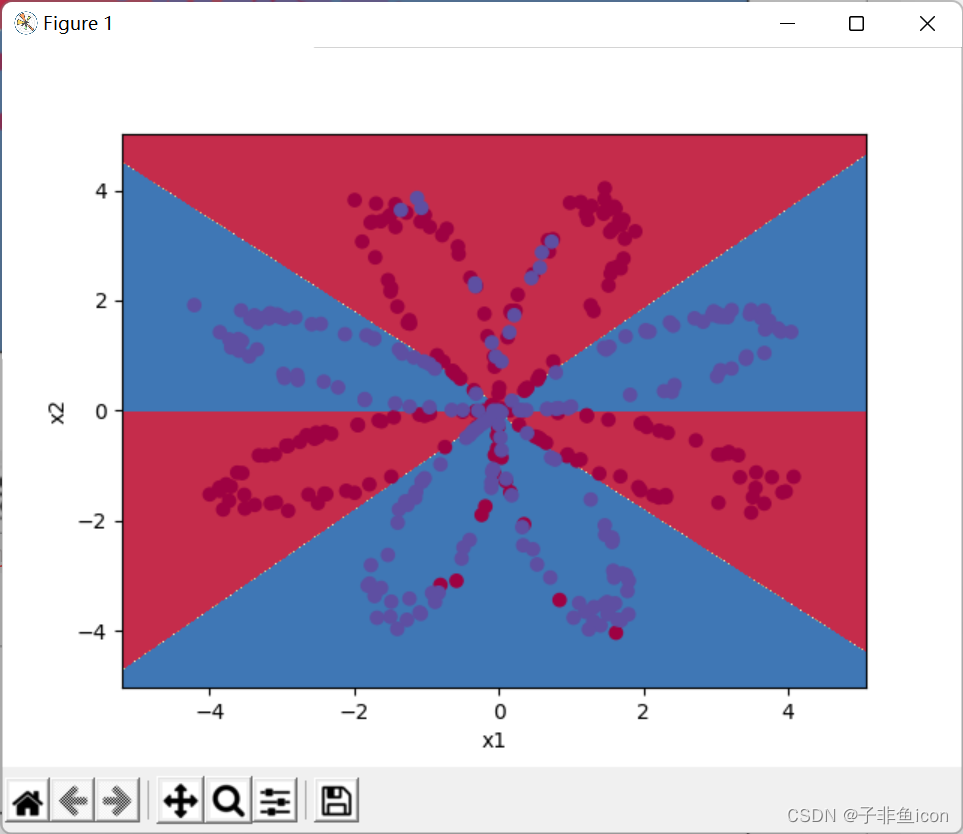
##############查看逻辑回归分类效果###################
clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X.T,Y.T)

plot_decision_boundary(lambda x: clf.predict(x), X, Y) #绘制决策边界
plt.title("Logistic Regression") #图标题
LR_predictions = clf.predict(X.T) #预测结果
# 这里计算正确率相当于是用内积，11得1，(1-0)*(1-0)也得1，相同则为1
print ("逻辑回归的准确性： %d " % float((np.dot(Y, LR_predictions) +
		np.dot(1 - Y,1 - LR_predictions)) / float(Y.size) * 100) +
       "% " + "(正确标记的数据点所占的百分比)")

################搭建神经网络###################

# 定义神经网络结构
def layer_sizes(X, Y):

	n_x = X.shape[0]  # 输入层的个数
	n_h = 4 # 隐藏层的个数
	n_y = Y.shape[0]  # 输出层的个数

	return n_x, n_h, n_y


# 初始化参数
def initialize_parameters(n_x, n_h, n_y):

	np.random.seed(2)
	W1 = np.random.randn(n_h, n_x)*0.01
	b1 = np.zeros((n_h, 1))
	W2 = np.random.randn(n_y, n_h)*0.01
	b2 = np.zeros((n_y, 1))

	parameters = {"W1":W1, "b1":b1, "W2":W2, "b2":b2}

	return parameters

# 前向传播
def forward_propagation(X, parameters):

	W1, b1, W2, b2 = parameters["W1"], parameters["b1"], parameters["W2"], parameters["b2"]
	Z1 = np.dot(W1, X) + b1
	A1 = np.tanh(Z1)
	Z2 = np.dot(W2, A1) + b2
	A2 = sigmoid(Z2)
	cache = {"Z1":Z1, "A1":A1, "Z2":Z2, "A2":A2}

	return A2, cache

# 计算损失
def compute_cost(A2, Y):

	m = Y.shape[1]
	cost = (-1/m)*np.sum(Y*np.log(A2) + (1-Y)*np.log(1-A2))
	cost = np.squeeze(cost)

	return cost

# 反向传播
def backward_propagation(parameters, cache, X, Y):

	m = X.shape[1]
	W2 = parameters["W2"]
	A1 = cache["A1"]
	A2 = cache["A2"]

	dZ2 = A2 - Y
	dW2 = (1/m)*np.dot(dZ2,A1.T)
	db2 = (1/m)*np.sum(dZ2, axis=1, keepdims=True)
	g1_grad = 1 - np.power(A1, 2)
	dZ1 = np.dot(W2.T, dZ2)*g1_grad
	dW1 = (1/m)*np.dot(dZ1, X.T)
	db1 = (1/m)*np.sum(dZ1, axis=1, keepdims=True)

	grads = {"dW1":dW1, "db1":db1, "dW2":dW2, "db2":db2}

	return grads

# 更新参数
def update_parameters(parameters, grads, learning_rate=1.2):

	W1 = parameters["W1"]
	W2 = parameters["W2"]
	b1 = parameters["b1"]
	b2 = parameters["b2"]

	dW1 = grads["dW1"]
	dW2 = grads["dW2"]
	db1 = grads["db1"]
	db2 = grads["db2"]

	W1 = W1 - learning_rate * dW1
	W2 = W2 - learning_rate * dW2
	b1 = b1 - learning_rate * db1
	b2 = b2 - learning_rate * db2

	parameters = {"W1":W1, "b1":b1, "W2":W2, "b2":b2}

	return parameters

# 整合模型
def nn_model(X, Y, n_h, num_iterations, print_cost = False):

	np.random.seed(3)  # 指定随机种子
	n_x = layer_sizes(X, Y)[0]
	n_y = layer_sizes(X, Y)[2]

	parameters = initialize_parameters(n_x, n_h, n_y)

	cost_ls = []
	for i in range(num_iterations):
		A2, cache = forward_propagation(X, parameters)
		cost = compute_cost(A2, Y)
		grads = backward_propagation(parameters, cache, X, Y)
		parameters = update_parameters(parameters, grads, learning_rate=0.5)


		if i % 500 == 0:
			cost_ls.append(cost)

		if print_cost:
			if i % 500 == 0:
				print("第", i, "次循环，成本为："+str(cost))

	return parameters, cost_ls

# 预测
def predict(parameters, X):

	A2, cache = forward_propagation(X, parameters)
	predictions = np.round(A2)

	return predictions

# 运行得到结果
parameters,cost_ls = nn_model(X, Y, n_h=4, num_iterations=10000, print_cost = True)


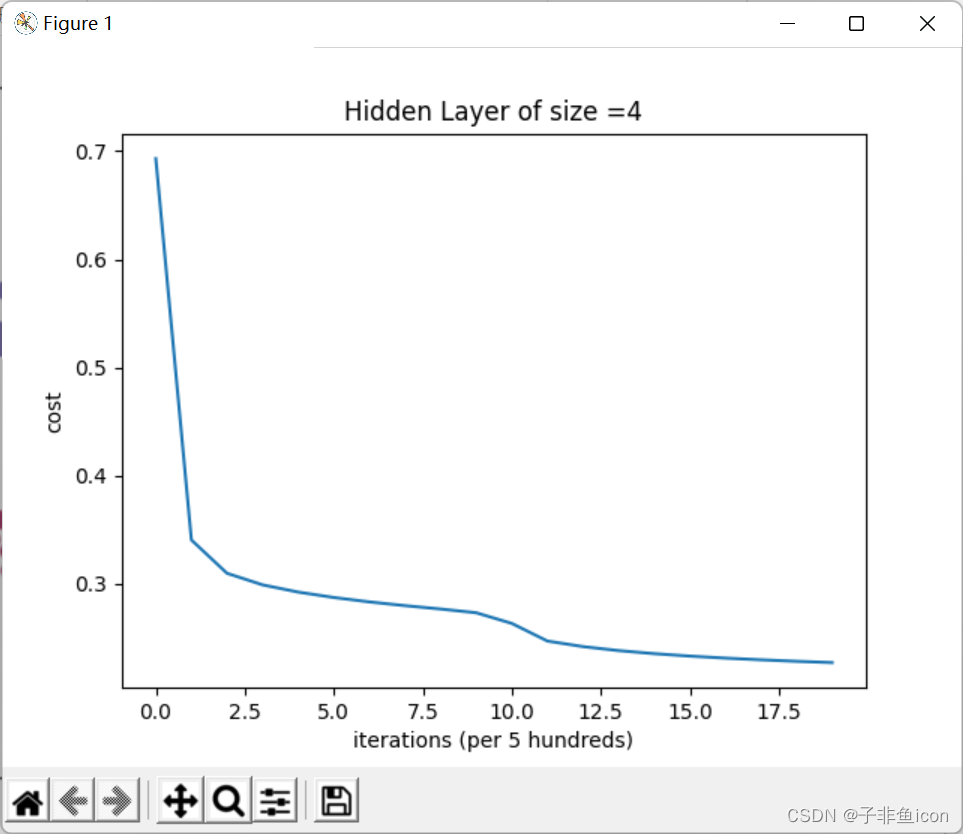
# 损失曲线
plt.plot(cost_ls)
plt.xlabel("iterations (per 5 hundreds)")
plt.ylabel("cost")
plt.title("Hidden Layer of size =" + str(4))
plt.show()

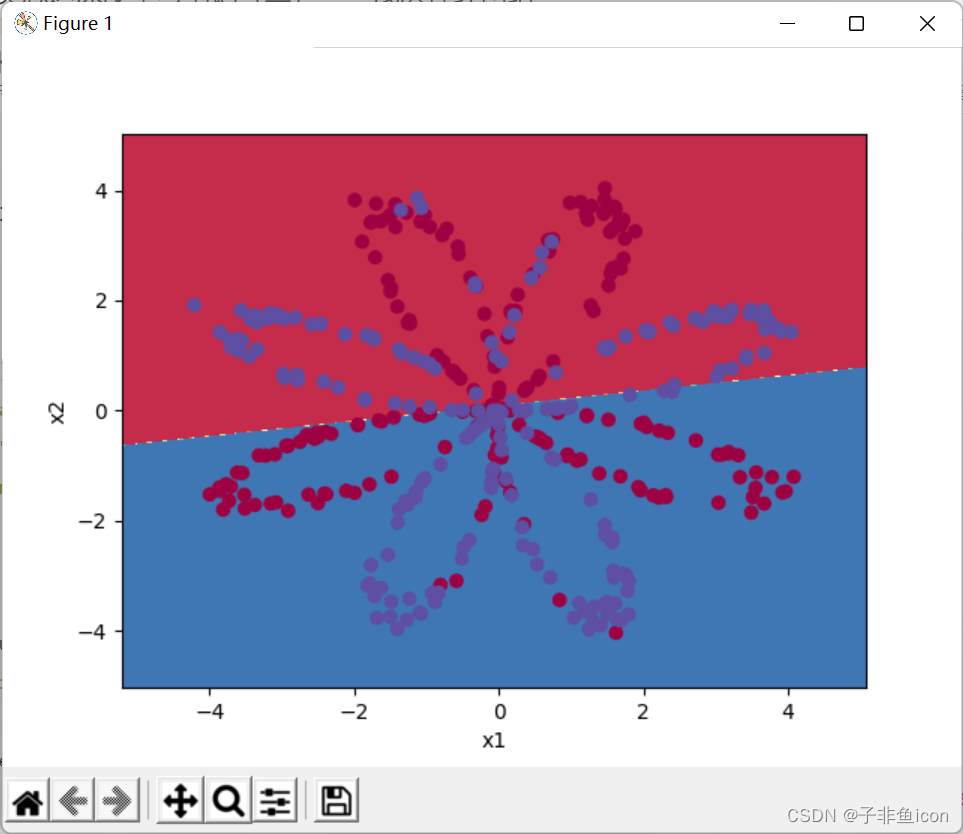
#绘制边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))

predictions = predict(parameters, X)
print("准确率：%d" %float((np.dot(Y, predictions.T) + np.dot(1-Y, 1-predictions.T)) / float(Y.size)*100) + "%")

输出结果：

X的维度： (2, 400)
Y的维度： (1, 400)
样本个数： 400
D:\Anaconda3\envs\pytorch\lib\site-packages\sklearn\utils\validation.py:63: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
  return f(*args, **kwargs)
逻辑回归的准确性： 47 % (正确标记的数据点所占的百分比)
第 0 次循环，成本为：0.6930480201239823
第 500 次循环，成本为：0.34060259042201396
第 1000 次循环，成本为：0.3098018601352803
第 1500 次循环，成本为：0.2990913402318003
第 2000 次循环，成本为：0.2924326333792647
第 2500 次循环，成本为：0.2874240978061956
第 3000 次循环，成本为：0.2833492852647412
第 3500 次循环，成本为：0.2798942641564122
第 4000 次循环，成本为：0.27678077562979253
第 4500 次循环，成本为：0.27332846125959825
第 5000 次循环，成本为：0.26347155088593094
第 5500 次循环，成本为：0.24718448655036185
第 6000 次循环，成本为：0.24204413129940758
第 6500 次循环，成本为：0.2383480507872823
第 7000 次循环，成本为：0.23552486626608762
第 7500 次循环，成本为：0.23327102545858774
第 8000 次循环，成本为：0.23140964509854278
第 8500 次循环，成本为：0.2298310973726687
第 9000 次循环，成本为：0.22846408048352362
第 9500 次循环，成本为：0.22726031625031515
准确率：90%

4.5 更改隐藏层节点数量

代码：

# 更改隐藏节点数量
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50] #隐藏层数量
for i, n_h in enumerate(hidden_layer_sizes):
    plt.subplot(4, 2, i + 1)
    plt.title('Hidden Layer of size %d' % n_h)
    parameters,_ = nn_model(X, Y, n_h, num_iterations=5000)
    plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
    predictions = predict(parameters, X)
    accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
    print ("隐藏层的节点数量： {}  ，准确率: {} %".format(n_h, accuracy))
plt.show()

结果：

隐藏层的节点数量： 1  ，准确率: 67.25 %
隐藏层的节点数量： 2  ，准确率: 66.5 %
隐藏层的节点数量： 3  ，准确率: 89.25 %
隐藏层的节点数量： 4  ，准确率: 90.0 %
隐藏层的节点数量： 5  ，准确率: 89.75 %
隐藏层的节点数量： 20  ，准确率: 90.0 %
隐藏层的节点数量： 50  ，准确率: 89.75 %

注：这里我在用pycharm实现的时候，发现这七张图是单独一张张的蹦出来的，并不能像参考链接那样显示在同一张图中，此处存疑。

不过我也出现了跟评论区一样的问题，就是最后两张图的边界并没有曲线部分

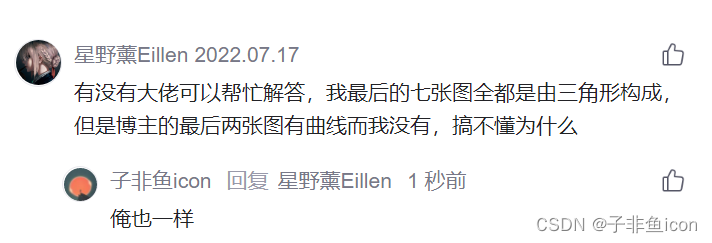
如下所示：

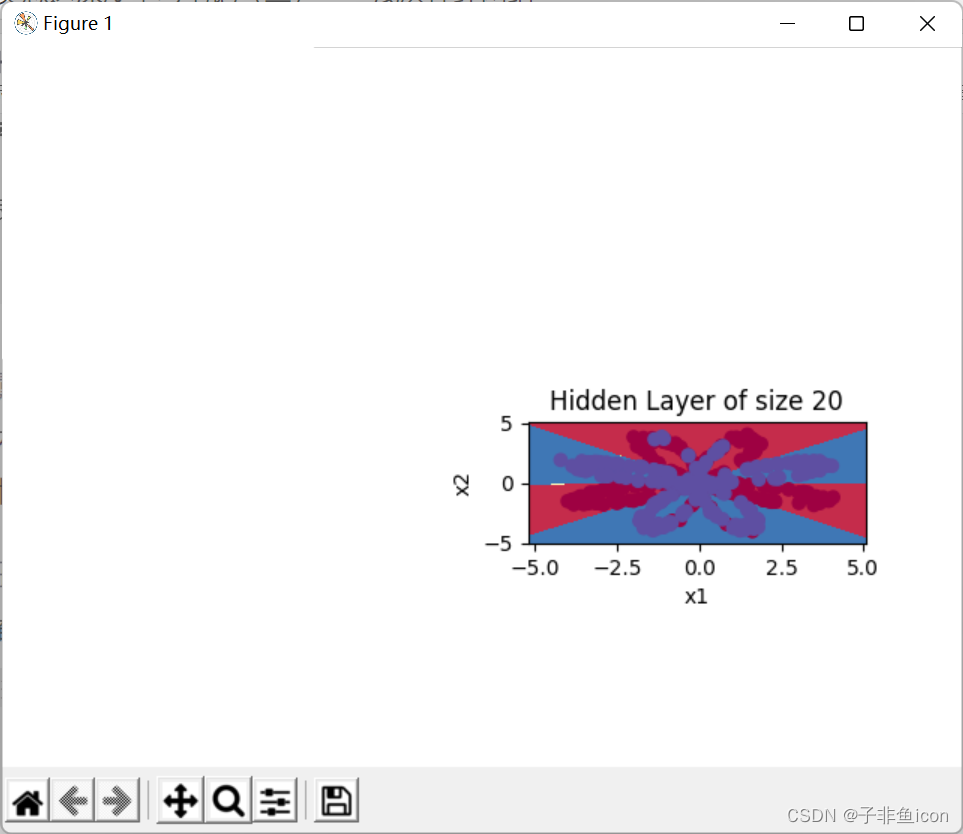
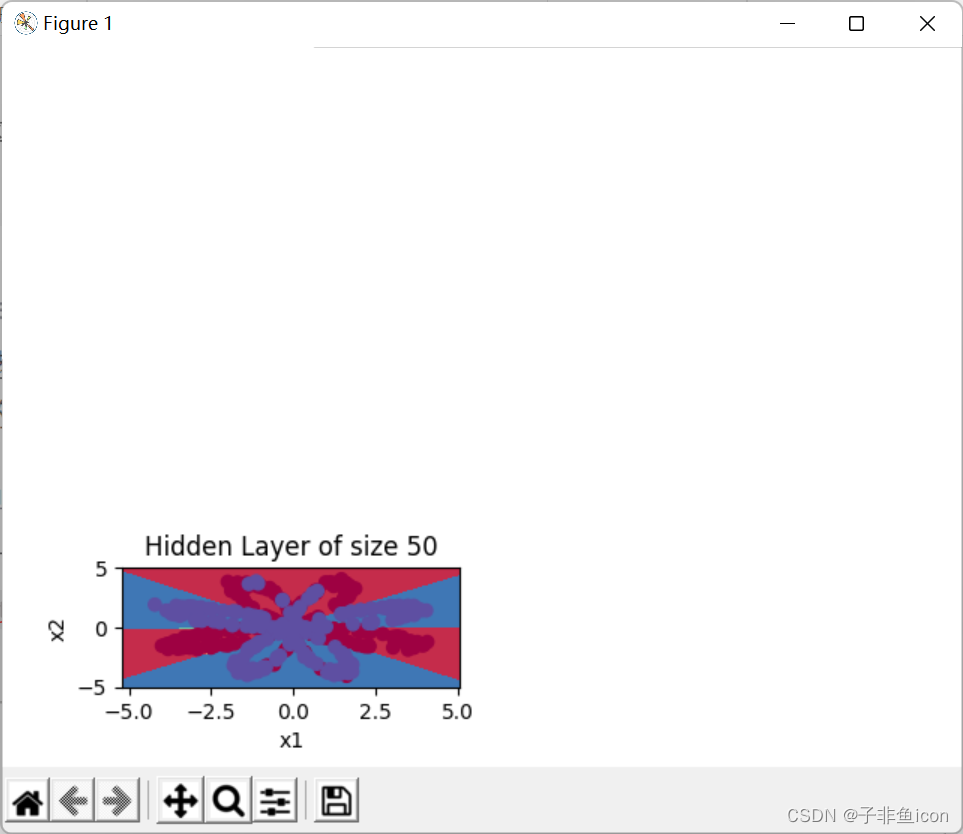
4.6 修改激活函数为sigmoid或ReLu

其他均不变， 修改为sigmoid:


结果：

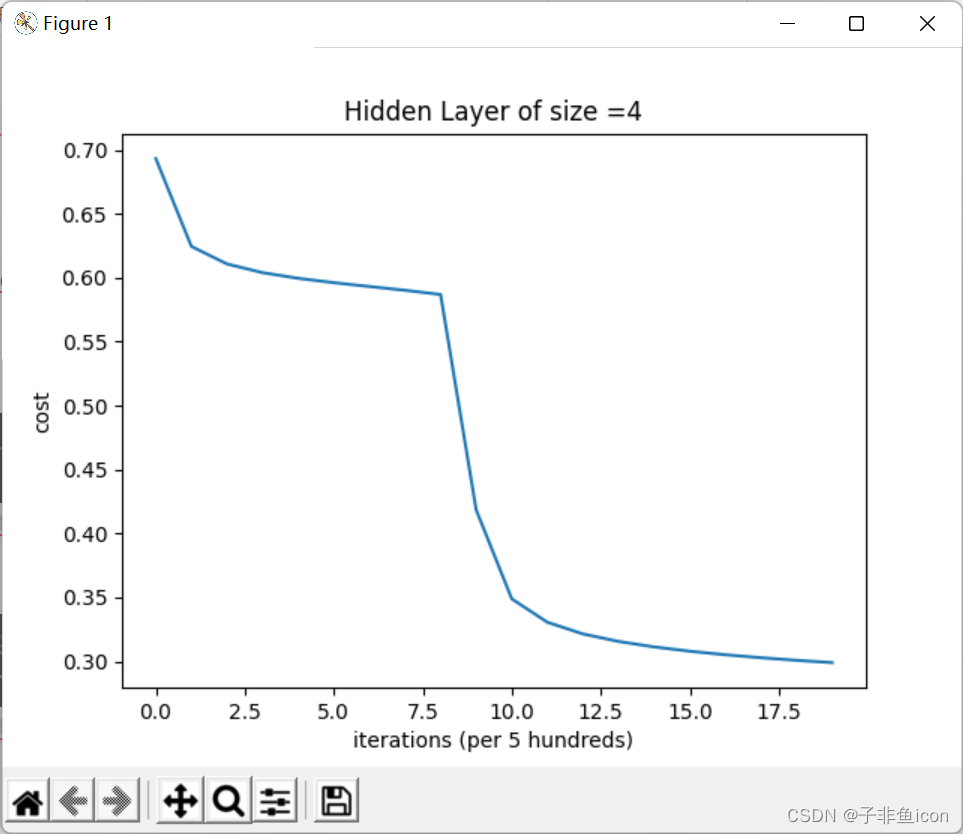
第 0 次循环，成本为：0.6931247519503794
第 500 次循环，成本为：0.6244657826970711
第 1000 次循环，成本为：0.6107222228158191
第 1500 次循环，成本为：0.6039371149408124
第 2000 次循环，成本为：0.5995084389140075
第 2500 次循环，成本为：0.596109901672873
第 3000 次循环，成本为：0.5931071583849431
第 3500 次循环，成本为：0.5901547609141053
第 4000 次循环，成本为：0.5868709574764808
第 4500 次循环，成本为：0.41841669134439097
第 5000 次循环，成本为：0.3488657656261514
第 5500 次循环，成本为：0.33057466470816593
第 6000 次循环，成本为：0.32144647880586485
第 6500 次循环，成本为：0.3155749134437513
第 7000 次循环，成本为：0.3112907354408687
第 7500 次循环，成本为：0.307932726197581
第 8000 次循环，成本为：0.30517808072043195
第 8500 次循环，成本为：0.30284596528485636
第 9000 次循环，成本为：0.3008250363286913
第 9500 次循环，成本为：0.29904194639617193
准确率：88%

可见准确率有所下降

修改为ReLU：

# 定义ReLU激活函数
def ReLU(z):

	s = np.maximum(z, 0)  # 逐元素比较大小
	return s

参考链接

参考链接

结果：

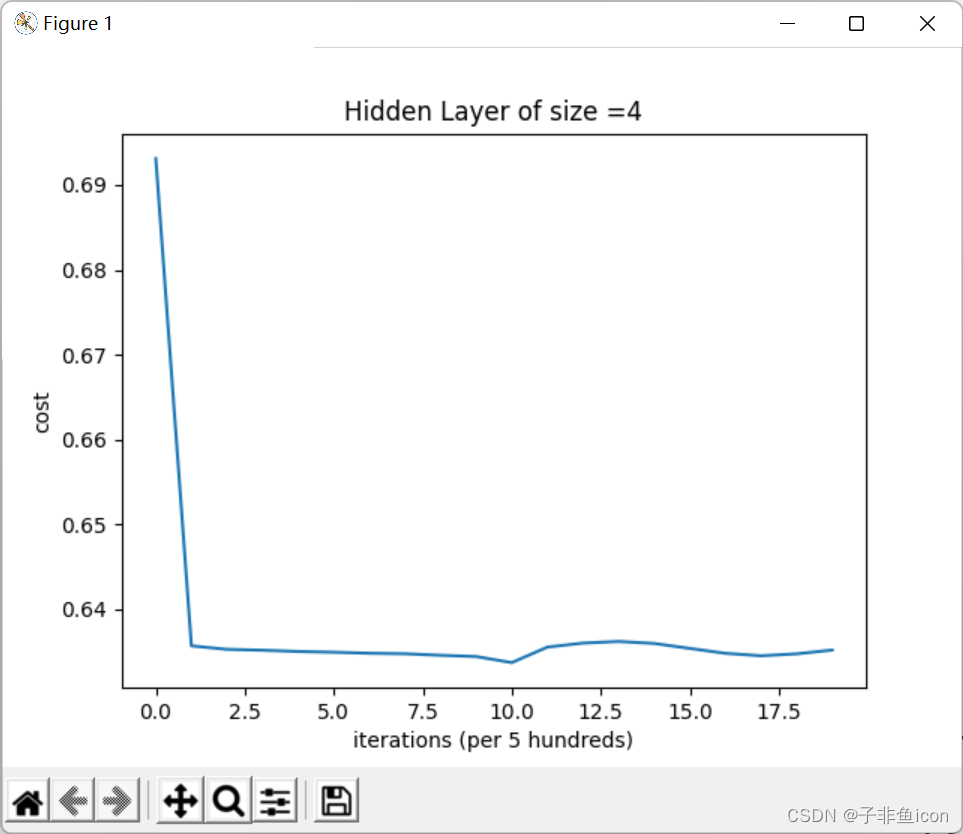
第 0 次循环，成本为：0.6930967698565371
第 500 次循环，成本为：0.6356874846902634
第 1000 次循环，成本为：0.6352750077434912
第 1500 次循环，成本为：0.6351694853292209
第 2000 次循环，成本为：0.6350258218835284
第 2500 次循环，成本为：0.6349349957137536
第 3000 次循环，成本为：0.6348157885388662
第 3500 次循环，成本为：0.6347537708872427
第 4000 次循环，成本为：0.6345750469619966
第 4500 次循环，成本为：0.6344264326858305
第 5000 次循环，成本为：0.6337141308981071
第 5500 次循环，成本为：0.6355398711975524
第 6000 次循环，成本为：0.6360123849095829
第 6500 次循环，成本为：0.6362029177098184
第 7000 次循环，成本为：0.6359693905471514
第 7500 次循环，成本为：0.6353845131275947
第 8000 次循环，成本为：0.6348067172668909
第 8500 次循环，成本为：0.6345169432949002
第 9000 次循环，成本为：0.6347454422513285
第 9500 次循环，成本为：0.6351892775200947
准确率：60%

结果跟一个评论差不多

准确率更低了，可能此时需要配合修改网络的深度和学习率等。

4.7 模型在其他数据集上的功能

代码：

# 加载和查看数据集
noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()

datasets = {"noisy_circles": noisy_circles,
            "noisy_moons": noisy_moons,
            "blobs": blobs,
            "gaussian_quantiles": gaussian_quantiles}

dataset = "noisy_moons"

X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])

if dataset == "blobs":
    Y = Y % 2

plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral)
plt.show()

结果：

逻辑回归的准确性： 86 % (正确标记的数据点所占的百分比)
第 500 次循环，成本为：0.31758137148324117
第 1000 次循环，成本为：0.31706344864332137
第 1500 次循环，成本为：0.31680315840616297
第 2000 次循环，成本为：0.31664865493768496
第 2500 次循环，成本为：0.3165463339611085
第 3000 次循环，成本为：0.3164733097990672
第 3500 次循环，成本为：0.31641831102038764
第 4000 次循环，成本为：0.31637516452244047
第 4500 次循环，成本为：0.316340211525548
第 5000 次循环，成本为：0.3163111497883384
第 5500 次循环，成本为：0.31628646146239126
第 6000 次循环，成本为：0.31626510730364255
第 6500 次循环，成本为：0.3162463526358023
第 7000 次循环，成本为：0.3162296631590514
第 7500 次循环，成本为：0.31621463996561683
第 8000 次循环，成本为：0.3162009776170841
第 8500 次循环，成本为：0.3161884363033835
第 9000 次循环，成本为：0.3161768228508027
第 9500 次循环，成本为：0.31616597740354435
第 10000 次循环，成本为：0.31615576377750754
准确率：86%

发现结果居然跟逻辑回归的一样，均为86%，说明，训练效果并不是很好。