本文质疑基于Transformer的长期时间序列预测（LTSF）解决方案的有效性。引入LTSF - Linear模型进行对比，在9个真实数据集实验中，LTSF - Linear表现优于现有基于Transformer的复杂模型。还对现有基于Transformer的解决方案各方面进行实证研究，为LTSF任务研究提供新思路。
系列文章目录
transformer对时间序列预测有效吗? AAAI23
文章目录
摘要
最近，针对长期时间序列预测(LTSF)任务，出现了大量基于变压器的解决方案。尽管在过去几年中取得了越来越多的成绩，但我们质疑这项工作中这条研究路线的有效性。具体来说，transformer可以说是提取长序列中元素之间语义相关性的最成功的解决方案。然而，在时间序列建模中，我们要从连续点的有序集合中提取时间关系。在变压器中使用位置编码和标记嵌入子序列有助于保留一些排序信息，但排列不变自关注机制的性质不可避免地导致了时间信息的丢失。
为了验证我们的说法，我们引入了一组令人尴尬的单层线性模型，称为LTSF-Linear进行比较。在9个真实数据集上的实验结果表明，LTSF- linear在所有情况下都令人惊讶地优于现有的基于变压器的复杂LTSF模型，并且通常有很大的优势。此外，我们进行了全面的实证研究，探讨了LTSF模型的各种设计元素对其时间关系提取能力的影响。我们希望这一惊人的发现为LTSF任务开辟了新的研究方向。我们还提倡在未来对其他时间序列分析任务(例如，异常检测)重新审视基于transformer的解决方案的有效性。
提示：以下是本篇文章正文内容
一、介绍
时间序列在当今数据驱动的世界中无处不在。鉴于历史数据，时间序列预测(TSF)是一项长期存在的任务，具有广泛的应用，包括但不限于交通流量估计，能源管理和金融投资。在过去的几十年里，TSF解决方案经历了从传统的统计方法(例如，ARIMA (Ariyo, Adewumi, and Ayo 2014))和机器学习技术(例如，GBRT (Friedman 2001))到基于深度学习的解决方案(例如，Bai, Kolter, and Koltun 2018;Liu et al. 2022)。
Transformer (Vaswani et al. 2017)可以说是最成功的序列建模架构，在各种应用中表现出无与伦比的性能，例如自然语言处理(NLP) (Devlin et al. 2018)，语音识别(Dong, Xu, and Xu 2018)和计算机视觉(Liu et al. 2021b)。最近，根据(Wen et al. 2022)的调查，基于变压器的时间序列分析解决方案也激增。最著名的模型，专注于较少探索和具有挑战性的长期时间序列预测(LTSF)问题，包括LogTrans (Li等人，2019)(NeurIPS 2019)， Informer (Zhou等人，2021)(AAAI 2021年最佳论文)，Autoformer (Xu等人，2021)(NeurIPS 2021)， Pyraformer (Liu等人，2021a) (ICLR 2022 Oral)，Triformer (Cirstea et al. 2022) (IJCAI 2022)和FEDformer (Zhou et al. 2022) (ICML 2022)。
变形金刚的主要工作动力来自于它的多头自注意机制，它具有显著的提取长序列元素之间语义相关性的能力(例如，文本中的单词或图像中的二维补丁)。然而，自我注意在一定程度上具有排列不变性和“反序性”。虽然使用各种类型的位置编码技术可以保留一些有序信息，但在其上加上自注意后，仍然不可避免地存在时间信息丢失。对于语义丰富的应用程序，如NLP，这通常不是一个严重的问题，例如，即使我们重新排序其中的一些单词，句子的语义也会在很大程度上保留下来。然而，在分析时间序列数据时，通常数值数据本身缺乏语义，我们主要感兴趣的是对连续点之间的时间变化进行建模。也就是说，秩序本身起着最关键的作用。因此，我们提出了以下有趣的问题:变形金刚对长期时间序列预测真的有效吗?
此外，虽然现有的基于变压器的LTSF解决方案已经证明了比传统方法有相当大的预测精度提高，但在他们的实验中，所有比较的(非变压器)基线都执行自回归或迭代多步骤(IMS)预测(Ariyo, Adewumi, and Ayo 2014;Salinas, Flunkert, and Gasthaus 2017;Bahdanau, Cho, and Bengio 2014;Taylor and Letham 2017)，众所周知，对于LTSF问题，它们会受到显著的误差累积效应的影响。因此，在这项工作中，我们用直接多步骤(DMS)预测策略挑战基于变压器的LTSF解决方案，以验证其真实性能。
并非所有的时间序列都是可预测的，更不用说长期预测了(例如，对于混沌系统)。我们假设长期预测只适用于那些趋势和周期性相对明显的时间序列。由于线性模型已经可以提取这些信息，我们引入了一组令人尴尬的简单模型，称为LTSF-Linear，作为比较的新基线。LTSF-Linear用单层线性模型对历史时间序列进行回归，直接预测未来时间序列。我们在九个广泛使用的基准数据集上进行了广泛的实验，这些数据集涵盖了各种现实生活中的应用:交通、能源、经济、天气和疾病预测。令人惊讶的是，我们的结果表明，LTSF-Linear在所有情况下都优于现有的基于复杂变压器的模型，并且通常有很大的优势(20% ~ 50%)。此外，我们发现，与现有的transformer中的声明相反，它们中的大多数不能从长序列中提取时间关系，即随着回看窗口大小的增加，预测误差并没有减少(有时甚至增加)。最后，我们对现有的基于变压器的TSF解决方案进行了各种烧蚀研究，以研究其中各种设计元素的影响。
综上所述，这项工作的贡献包括:
•据我们所知，这是第一个挑战蓬勃发展的变形金刚在长期时间序列预测任务中的有效性的工作。
•为了验证我们的说法，我们引入了一组令人尴尬的单层线性模型，命名为ltslinear，并在9个基准上将它们与现有的基于transformer的LTSF解决方案进行比较。LTSF- linear可以作为LTSF问题的新基线。
•我们对现有基于transformer的解决方案的各个方面进行了全面的实证研究，包括长输入建模的能力、对时间序列顺序的敏感性、位置编码和子序列嵌入的影响以及效率比较。我们的发现将有益于这一领域的未来研究。
综上所述，我们得出结论，transformer对时间序列的时间建模能力被夸大了，至少对于现有的LTSF基准来说是这样。与此同时，虽然LTSF-Linear的预测精度比现有的作品更好，但它只是一个简单的基线，用于未来研究具有挑战性的长期TSF问题。根据我们的发现，我们还提倡在未来对其他时间序列分析任务(例如，异常检测)重新审视基于transformer的解决方案的有效性。
二、初论:TSF问题制定
对于包含C变量的时间序列，给定历史数据 X = { X 1 t , . . . , X C t } t = 1 L , \mathcal{X}=\{X_{1}^{t},...,X_{C}^{t}\}_{t=1}^{L}, X={X1t,...,XCt}t=1L,，其中L为回看窗口大小， X i t X_i^{t} Xit为第i个变量在第t个时间步长的值。时间序列预测任务是预测值 X ^ ˉ = { X ^ 1 t , . . . , X ^ C t } t = L + 1 L + T \bar{\hat{\mathcal X}}=\{\hat{X}_{1}^{t},...,\hat{X}_{C}^{t}\}_{t=L+1}^{L+T} X^ˉ={X^1t,...,X^Ct}t=L+1L+T在未来T个时间步长。当T > 1时，迭代多步(IMS)预测[23]学习到一个单步预测器，并迭代地应用它来获得多步预测。另一种方法是直接多步预测(DMS)，[4]直接对多步预测目标进行一次优化。
与DMS预测结果相比，IMS预测结果由于采用自回归估计过程，方差较小，但不可避免地存在误差累积效应。因此，当存在高度精确的单步预测器且T相对较小时，IMS预测更可取。相比之下，当难以获得无偏单步预测模型或T较大时，DMS预测产生更准确的预测。
三、 变压器LTSF解决方案
由于多头自注意机制的有效性，基于变压器的模型[26]在自然语言处理和计算机视觉领域的许多长期人工智能任务中取得了无与伦比的表现。这也引发了许多基于transformer的时间序列建模技术的研究兴趣[20,27]。特别是，大量的研究工作致力于LTSF任务(例如，[16,18,28,30,31])。考虑到使用Transformer模型捕获长期依赖关系的能力，它们中的大多数都集中在较少探索的长期预测问题( T ≫ 1 T\gg1 T≫1)1上。
当将普通Transformer模型应用于LTSF问题时，它存在一些局限性，包括原始自注意方案的二次时间/内存复杂度以及自回归解码器设计引起的误差累积。Informer[30]解决了这些问题，并提出了一种具有较低复杂性和DMS预测策略的新颖Transformer体系结构。后来，更多的Transformer变体在其模型中引入了各种时间序列特征以提高性能或效率[18,28,31]。我们将现有的基于变压器的LTSF解决方案的设计元素总结如下(参见图1)。
图1。现有的基于变压器的TSF解决方案的管道。在(a)和(b)中，实线框为基本操作，虚线框为可选应用。©和(d)对于不同的方法是不同的[16,18,28,30,31]。
时间序列分解:对于数据预处理，零均值归一化在TSF中很常见。此外，Autoformer[28]首先在每个神经块后面应用季节趋势分解，这是时间序列分析中的标准方法，使原始数据更具可预测性[6,13]。具体来说，他们在输入序列上使用移动平均核来提取时间序列的趋势周期成分。将原始序列与趋势分量之差作为季节分量。在Autoformer分解方案的基础上，FEDformer[31]进一步提出了混合专家策略，将不同核大小的移动平均核提取的趋势分量进行混合。
输入嵌入策略:Transformer体系结构中的自关注层不能保存时间序列的位置信息。然而，局部位置信息，即时间序列的排序，是重要的。此外，全局时间信息，如分层时间戳(周、月、年)和不可知时间戳(假日和事件)，也是信息性的[30]。为了增强时间序列输入的时间上下文，基于SOTA变换的方法的一个实用设计是在输入序列中注入几个嵌入，如固定位置编码、通道投影嵌入和可学习的时间嵌入。此外，还引入了带有时间卷积层[16]或可学习时间戳[28]的时间嵌入。
自我关注设计: 转换器依靠自关注机制来提取成对元素之间的语义依赖关系。为了减少普通变压器的 O ( L 2 ) O\left(L^{2}\right) O(L2)时间和内存复杂性，最近的研究提出了两种提高效率的策略。一方面，LogTrans和Pyraformer明确地在自关注方案中引入了稀疏性偏差。具体来说，LogTrans使用log稀疏掩码将计算复杂度降低到 O ( L l o g L ) O\left(LlogL\right) O(LlogL)，而Pyraformer采用金字塔式注意力，以O (L)的时间和内存复杂度捕获分层多尺度时间依赖性。另一方面，Informer和FEDformer利用了自关注矩阵的低秩特性。Informer提出了ProbSparse自关注机制和自关注提取操作，将复杂度降低到 O ( L l o g L ) O\left(LlogL\right) O(LlogL); FEDformer设计了随机选择的傅里叶增强块和小波增强块，使复杂度达到0 (L)。最后，Autoformer设计了一种串联自相关机制来取代原有的自关注层。
解码器:普通的Transformer解码器以自回归的方式输出序列，导致推理速度慢和错误累积效应，特别是对于长期预测。Informer为DMS预测设计了一种生成式解码器。其他Transformer变体采用类似的DMS策略。例如，Pyraformer使用一个连接时空轴的全连接层作为解码器。Autoformer将趋势周期分量和季节分量的叠加自相关机制两种特征进行精细化分解，得到最终预测结果。FEDformer还使用一种分解方案与提出的频率注意块解码最终结果。
Transformer模型的前提是配对元素之间的语义相关性，而自关注机制本身是排列不变的，其建模时间关系的能力在很大程度上取决于与输入标记相关联的位置编码。考虑到时间序列中的原始数值数据(例如，股票价格或电力价值)，它们之间几乎没有任何逐点的语义相关性。在时间序列建模中，我们主要关心的是一组连续点之间的时间关系，而这些元素的顺序而不是配对关系起着最关键的作用。虽然使用位置编码和标记嵌入子序列有利于保留一些排序信息，但排列不变自注意机制的性质不可避免地导致了时间信息的丢失。由于上述观察结果，我们有兴趣重新审视基于变压器的LTSF解决方案的有效性。
四、An Embarrassingly Simple Baseline
在现有的基于变压器的LTSF解决方案(
T
≫
1
T\gg1
T≫1)的实验中，所有比较的(非变压器)基线都是IMS预测技术，已知其存在显着的误差累积效应。我们假设这些工作中的性能改进主要是由于其中使用的DMS策略。
为了验证这一假设，我们通过一个名为LTSF-Linear的时间线性层提出了最简单的DMS模型，作为比较的基线。ltslinear的基本公式是通过加权和运算直接回归历史时间序列进行未来预测(如图2所示)。其数学表达式为
X
^
i
=
W
X
i
,
\hat{X}_{i}=WX_{i},
X^i=WXi,，其中
W
∈
R
T
×
L
W\in\mathbb{R}^{T\times L}
W∈RT×L是沿时间轴的线性层。
X
^
i
\hat{X}_{i}
X^i和
X
i
{X}_{i}
Xi是每个
i
t
h
i_{th}
ith变量的预测和输入。请注意，LTSF-Linear在不同变量之间共享权重，并且不为任何空间相关性建模。
LTSF-Linear是一组线性模型。Vanilla Linear是一个单层线性模型。为了处理跨不同领域(例如，金融、交通和能源领域)的时间序列，我们进一步引入了两种具有两种预处理方法的变体，称为DLinear和NLinear。
•具体来说，DLinear是一种结合了Autoformer和FEDformer中使用的线性层分解方案。它首先通过移动平均核和剩余(季节)分量将原始数据输入分解为趋势分量。然后，对每个分量应用两个单层线性层，将两个特征相加得到最终的预测结果。通过显式地处理趋势，当数据中有明显的趋势时，DLinear增强了普通线性的性能。
•同时，为了提高LTSF-Linear在数据集中出现分布移位时的性能，NLinear首先用序列的最后一个值减去输入。然后，输入经过一个线性层，在进行最终预测之前，将减去的部分加回来。NLinear中的减法和加法是输入序列的简单归一化。
五、实验
5.1. 实验设置
数据集。我们在九个广泛使用的现实世界数据集上进行了广泛的实验，包括ETT(电力变压器温度)[30](ETTh1, ETTh2, ETTm1, ETTm2)，交通，电力，天气，ILI, ExchangeRate[15]。它们都是多元时间序列。我们在附录中留下了数据描述。
评估指标。根据之前的工作[28,30,31]，我们使用均方误差(MSE)和平均绝对误差(MAE)作为比较性能的核心指标。
比较方法。我们包括五种最新的基于变压器的方法:FEDformer [31]， Autoformer [28]， Informer [30]， Pyraformer[18]和LogTrans[16]。此外，我们还包含了一个简单的DMS方法:nearest Repeat (Repeat)，它重复回看窗口中的最后一个值，作为另一个简单的基线。由于FEDformer有两种变体，我们比较了精度更高的一种(通过傅里叶变换的FEDformer-f)。
5.2. 与变压器的比较
定量结果。在表2中，我们根据之前的工作[28,30,31]的实验设置，在9个基准上对上述所有变压器进行了广泛的评估。令人惊讶的是，在大多数情况下，LTSF-Linear的性能比SOTA FEDformer在多变量预测上提高了20% ~ 50%，其中ltslinear甚至不模拟变量之间的相关性。对于不同的时间序列基准，NLinear和DLinear在处理分布移位和趋势季节性特征方面表现出优势。我们还在附录中提供了ETT数据集的单变量预测结果，其中LTSF- linear仍然在很大程度上优于基于transformer的LTSF解决方案。
FEDformer在ETTh1上实现了具有竞争力的预测精度。这是因为FEDformer采用了经典的时间序列分析技术，如频率处理，这带来了时间序列的归纳偏置，有利于时间特征提取的能力。总之，这些结果表明，现有的基于复杂变压器的LTSF解决方案在现有的9个基准测试中似乎并不有效，而LTSF- linear可能是一个强大的基准。
另一个有趣的观察结果是，尽管朴素的Repeat方法在预测长期季节性数据(例如电力和交通)时显示出较差的结果，但它在汇率方面的表现出人意料地优于所有基于transformer的方法(约45%)。这主要是由于基于transformer的解决方案对趋势的错误预测，可能会对训练数据中的突然变化噪声过拟合，从而导致显著的精度下降(见图3(b))。相反，Repeat没有偏见。
定性结果。如图3所示，我们在三个选择的时间序列数据集上绘制了基于变压器的解决方案和ltcf - linear的预测结果:电力(序列1951，变量36)，汇率(序列676，变量3)和ETTh2(序列1241，变量2)，其中这些数据集具有不同的时间模式。当输入长度为96步，输出视界为336步时，变压器[28,30,31]无法捕获未来电力和ETTh2数据的尺度和偏差。此外，他们很难预测汇率等非周期性数据的正确趋势。这些现象进一步表明现有的基于变压器的LTSF任务解决方案的不足之处。
表2。就MSE和MAE而言，多变量长期预测误差越低越好。其中，ILI数据集预测视界T∈{24,36,48,60}。对于其他的，T∈{96,192,336,720}。Repeat重复回顾窗口中的最后一个值。最好的结果用粗体突出显示，变形金刚的最好结果用下划线突出显示。因此，与基于变压器的解决方案的结果相比，线性模型的结果是最好的。
5.3 LSTF 变压器的进一步分析
现有的ltsf - transformer能否很好地从较长的输入序列中提取时间关系?回顾窗口的大小极大地影响了预测的准确性，因为它决定了我们能从历史数据中学到多少。一般来说，一个强大的TSF模型，具有较强的时间关系提取能力，应该能够在更大的回看窗口尺寸下获得更好的结果。
为了研究输入回看窗口大小的影响，我们使用L∈{24,48,72,96,120,144,168,192,336,504,672,720}进行长期预测实验(T=720)。图4展示了两个数据集上的MSE结果。与先前研究的观察结果相似[27,30]，现有的基于transformer的模型的性能随着回看窗口大小的增加而恶化或保持稳定。相比之下，所有LTSF-Linear的性能都随着回看窗口大小的增加而显著提高。因此，如果给定较长的序列，现有的解决方案倾向于过拟合时间噪声而不是提取时间信息，并且输入大小为96正好适用于大多数变压器。此外，我们在附录中提供了更多的定量结果，我们的结论几乎适用于所有情况。
图3。电力、汇率和ETTh2上五个模型的长期预测输出(y轴)分别为输入长度L=96和输出长度T=192 (x轴)。
图4。在交通和电力数据集上，不同回望窗大小模型(x轴)的长期预测(T=720)的均方误差结果(y轴)。
我们可以从长期预测中学到什么?虽然回顾窗口中的时间动态对短期时间序列预测的准确性有显著影响，但我们假设长期预测仅取决于模型是否能够很好地捕捉趋势和周期性。也就是说，预测范围越远，回顾窗口本身的影响就越小。
为了验证上述假设，在表3中，我们比较了来自两个不同回顾窗口的数据对相同未来720时间步的预测精度:(i)原始输入L=96设置(称为Close)和(ii)原始96时间步之前的远输入L=96设置(称为far)。从实验结果来看，SOTA变压器的性能略有下降，表明这些模型仅从相邻的时间序列序列中捕获相似的时间信息。由于捕获数据集的内在特征通常不需要大量的参数，例如。一个参数可以表示周期性。使用太多的参数甚至会导致过拟合，这部分解释了为什么ltslinear比基于变压器的方法表现得更好。
自我关注计划对长期养老基金是否有效?我们验证现有Transformer(例如，Informer)中的这些复杂设计是否必要。在表4中，我们逐步将Informer转换为Linear。首先，我们将每个自注意层替换为一个线性层，称为at .- linear，因为自注意层可以被视为一个权值动态变化的全连接层。此外，我们在Informer中抛弃了其他辅助设计(例如FFN)，留下嵌入层和线性层，称为Embed + linear。最后，我们将模型简化为一个线性层。令人惊讶的是，Informer的性能随着逐渐简化而增长，这表明至少对于现有的LTSF基准测试来说，自关注方案和其他复杂模块是不必要的。
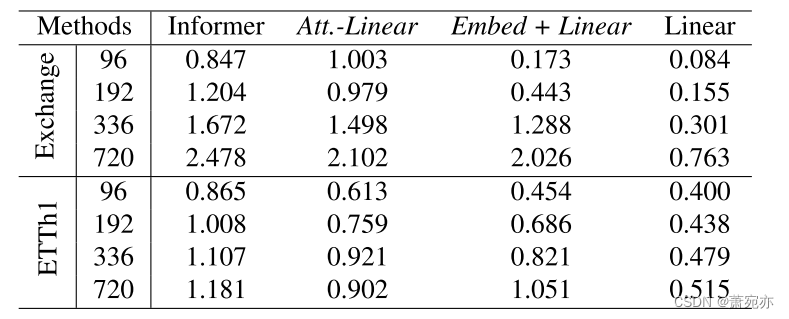
表4。从左到右列逐步将信息源变换为线性的MSE比较。at - linear是一种用线性层代替每个注意层的结构。嵌入+线性是放弃其他设计，只保留嵌入层和线性层。回望窗口的大小是96。
现有的ltsf变压器能很好地保持时间顺序吗?自我关注本质上是排列不变的，也就是说，与顺序无关。然而，在时间序列预测中，序列顺序往往起着至关重要的作用。我们认为，即使使用位置和时间嵌入，现有的基于transformer的方法仍然遭受时间信息丢失。在表5中，我们在嵌入策略之前对原始输入进行洗牌。提出了两种洗牌策略:洗牌;随机洗牌整个输入序列和Half-Ex。将输入序列的前半部分与后半部分交换。有趣的是，与Exchange Rate的原始设置(Ori.)相比，即使在随机打乱输入序列时，所有基于transformer的方法的性能也不会波动。相反，LTSF-Linear的性能会受到严重损害。这表明具有不同位置和时间嵌入的ltsf - transformer保留了相当有限的时间关系，并且容易对有噪声的金融数据进行过拟合，而LTSF-Linear可以自然地对顺序进行建模，并避免使用较少的参数进行过拟合。
表5。对原始输入序列进行洗牌时模型的MSE比较。闭嘴。随机打乱输入序列。半ex。将输入序列的前半部分与后半部分随机交换。平均下降是在洗牌后所有预测长度下的平均性能下降。所有结果均为5次运行的平均测试MSE。
对于ETTh1数据集，FEDformer和Autoformer在他们的模型中引入了时间序列归纳偏置，使得他们可以在数据集具有比汇率更明确的时间模式(例如，周期性)时提取某些时间信息。因此，两台变压器在关闭工况下的平均降幅分别为73.28%和56.91%。设置，它会丢失整个订单信息。此外，Informer在这两种情况下受到的影响都较小。和半ex。设置，由于它没有这种时间归纳偏差。总的来说，在所有情况下，LTSF-Linear的平均下降都大于基于变压器的方法，这表明现有的变压器不能很好地保持时间顺序。
不同的嵌入策略效果如何?我们研究了在基于变压器的方法中使用位置和时间戳嵌入的好处。在表6中，没有位置嵌入(wo/Pos.)， Informer的预测误差大大增加。没有时间戳嵌入(wo/Temp.)会随着预测长度的增加而逐渐损害Informer的性能。由于Informer对每个令牌使用单个时间步长，因此有必要在令牌中引入时态信息。
表6。基于transformer的不同嵌入策略在回顾窗口大小为96和预测长度为{96,192,336,720}情况下的MSE比较。
FEDformer和Autoformer不是在每个令牌中使用单个时间步长，而是输入一系列时间戳来嵌入时间信息。因此，它们可以在没有固定位置嵌入的情况下获得相当甚至更好的性能。然而，如果没有时间戳嵌入，由于全局时间信息的丢失，自耦器的性能会迅速下降。相反，由于FEDformer中提出的频率增强模块引入了时间感应偏置，因此移除任何位置/时间戳嵌入的影响较小。
训练数据大小是现有ltsftransformer的限制因素吗?有些人可能会认为基于transformer的解决方案的低性能是由于基准数据集的小尺寸。与计算机视觉或自然语言处理任务不同，TSF是在收集的时间序列上执行的，很难扩大训练数据的规模。事实上，训练数据的大小确实会对模型的性能产生重大影响。因此，我们对Traffic进行了实验，比较了在完整数据集(17544 *0.7小时)上训练的模型的性能，命名为Ori。，在缩短的数据集(8,760小时，即1年)上进行训练，称为Short。出乎意料的是，表7显示，在大多数情况下，减少训练数据的预测误差更低。这可能是因为全年数据比较长但不完整的数据具有更清晰的时间特征。虽然我们不能得出我们应该使用更少的数据进行训练的结论，但它表明训练数据规模不是Autoformer和FEDformer性能的限制原因。
表7。两种训练数据大小的MSE比较。
效率真的是头等大事吗?现有的LTSFTransformer声称，对于LTSF问题来说，普通Transformer的复杂度是无法承受的。虽然他们证明能够将理论上的时间和内存复杂度从O (L)提高到O (L)，但目前尚不清楚1)设备上的实际推理时间和内存成本是否得到改善，以及2)内存问题对于今天的GPU(例如，这里的NVIDIA Titan XP)来说是不可接受的和紧迫的。在表8中，我们比较了5次运行的平均实际效率。有趣的是，与普通Transformer(使用相同的DMS解码器)相比，大多数Transformer变体在实践中会产生相似甚至更差的推理时间和参数。这些后续工作引入了更多额外的设计元素，使实际成本更高。此外，即使输出长度为L = 720，普通Transformer的内存成本实际上也是可以接受的，这削弱了开发内存效率高的Transformer的重要性，至少对于现有的基准测试来说是这样。
表8。ltsf变压器在L=96和T=720条件下的实际效率比较。mac是乘法累加操作的个数。我们使用线性进行比较，因为它的代价是LTSF-Linear的两倍。推理时间平均为5次运行。
六、 结论及未来工作
结论。这项工作质疑了新兴的基于变压器的解决方案对长期时间序列预测问题的有效性。我们使用一个令人尴尬的简单线性模型LTSF-Linear作为DMS预测基线来验证我们的主张。请注意，我们的贡献不是来自于提出一个线性模型，而是来自于抛出一个重要的问题，展示令人惊讶的比较，并从不同的角度展示为什么ltsftransformer不像这些作品中声称的那样有效。我们真诚地希望我们的全面研究能够对未来在这方面的工作有所帮助。
未来的工作。LTSF-Linear具有有限的模型容量，它仅仅为未来的研究提供了一个简单但具有竞争力的基线，具有很强的可解释性。例如，单层线性网络很难捕捉由变化点[25]引起的时间动态。因此，我们相信在新的模型设计、数据处理和基准测试方面有很大的潜力来解决具有挑战性的LTSF问题。
扫一扫
887
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
