系列文章目录
U-Mixer:一种具有平稳性校正的 Unet-Mixer 架构,用于时间序列预测 AAAI22024
摘要
时间序列预测是各个领域的一项关键任务。 由于趋势、季节性或不规则波动等因素的影响,时间序列常常表现出非平稳性。 它阻碍了深层特征的稳定传播,破坏了特征分布,并使学习数据分布变化变得复杂。 因此,许多现有模型难以捕捉潜在模式,导致预测性能下降。 在这项研究中,我们使用我们提出的名为 U-Mixer 的框架来应对时间序列预测中非平稳性的挑战。 通过结合 Unet 和 Mixer,U-Mixer 有效地分别捕获不同块和通道之间的局部时间依赖性,以避免通道之间分布变化的影响,并合并低级和高级特征以获得全面的数据表示。 关键贡献是一种新颖的平稳性校正方法,通过约束模型处理前后数据之间的平稳性差异来显式恢复数据分布,以恢复非平稳性信息,同时确保保留时间依赖性。 通过对各种真实时间序列数据集的广泛实验,U-Mixer 展示了其有效性和鲁棒性,并比最先进的 (SOTA) 方法分别实现了 14.5% 和 7.7% 的改进。
一、引言
时间序列预测在金融(Ma et al. 2022)、天气预报(Liu et al. 2022a)和传感器数据分析(Zhao et al. 2023)等各个领域发挥着至关重要的作用。 提取有意义的模式、了解时间序列的潜在动态以预测未来趋势对于明智决策和有效解决问题至关重要(Zhang、Guo 和 Wang 2023)。 随着深度学习的出现,卷积神经网络(CNN)(Fukushima 1980)和 Transformers(Vaswani 等人,2017)在捕获时间依赖性和从时间序列中提取特征方面取得了显着的进展。 最近,最初为视觉任务引入的混合器架构(Tolstikhin et al. 2021)因其在顺序数据中建模复杂关系的能力而受到关注。 然而,Mixer应用于时间序列预测也面临着挑战。 时间序列数据通常表现出由趋势、季节性或不规则波动等因素引起的非平稳性。 这种属性会阻碍准确的建模和预测,从而限制 Mixer 架构的有效性。 在处理非平稳时,Mixer主要存在以下三个问题:(1)Mixer的深层结构导致浅层特征传播不稳定。 当信息流经多层时,低层特征的传输变得不稳定。 (2)由于通道之间存在显着的分布变化,不同通道的混合特征提取导致非平稳特征分布。 (3)模型训练无法直观地学习数据分布的变化,导致预测值的分布发生偏移和非平稳。
在本文中,我们提出 U-Mixer 来解决时间序列预测中的非平稳性问题。 U-Mixer结合了Unet和Mixer架构的优点来捕获不同级别的局部时间模式,同时单独处理时间和通道交互。 U-Mixer的关键贡献在于新颖的平稳性校正技术,该技术通过校正数据的平稳性来显式地恢复数据的分布。
具体来说,我们将时间序列划分为一些补丁,并使用 Mixer 架构独立处理它们。 这种基于补丁的处理允许对时间模式进行本地化分析并捕获数据中的细粒度细节。 Mixer 通过多层感知器(MLP)块有效地捕获不同补丁和通道之间的依赖关系,而不破坏整体时间序列,并从整个时间序列中学习有意义的表示。 同时,它单独处理时间交互和通道交互,避免了不同通道之间数据分布的显着变化导致的特征不稳定。 与MLP-Mixer不同的是,U-Mixer采用Unet架构,融合低层和高层特征,获得更全面、更丰富的数据表示,从而提高对数据的理解和建模能力。 此外,为了提高模型性能,时间序列通常会经历平稳化过程。 然而,由于非平稳信息的丢失,模型无法直观地学习数据分布的变化,导致预测值分布发生偏移。 通过训练学习数据分布的映射本质上是一个挑战。 因此,我们提出了一种平稳性校正方法,通过约束模型处理前后数据之间的平稳性差异来恢复非平稳信息,同时考虑数据的时间依赖性。
我们的贡献总结为
• 我们提出了U-Mixer 一种新的时间序列预测框架,可以捕获不同级别的局部时间模式并分别处理时间和通道交互。
• 我们提出了一种平稳性校正方法,通过约束模型处理前后的平稳性差异,显式地恢复数据的非平稳性信息,同时确保数据内的时间依赖性。
• U-Mixer采用Unet架构,融合低层和高层特征,使得数据的表达更加全面、丰富。
• 我们通过对各种真实时间序列数据集进行大量实验,证明了 UMixer 的有效性和鲁棒性。
二、Related Work
Time Series Prediction
时间序列预测是根据一组历史观察结果预测一个或多个变量的未来值的任务。 传统的统计方法和机器学习方法已被广泛使用,但尽管它们简单且可解释,但仍难以应对复杂的非线性模式。 近年来,深度学习模型已针对此任务进行了广泛研究。 尤其是长短期记忆(LSTM)(Hochreiter 和 Schmidhuber 1997),循环神经网络(RNN)的一种著名变体,被广泛应用于时间序列预测。 然而,它们可能会遭受梯度消失或爆炸的影响,从而限制了它们捕获长期依赖性的能力。 卷积神经网络(CNN)(Zhao et al. 2023)也适用于这项任务,通过提取局部模式并识别不同时间步长的相关特征。 基于 CNN 的模型在捕获数据中的空间和时间依赖性方面显示出了有希望的结果。
最近,基于 Transformer 的模型(Zhou et al. 2021;Wu et al. 2021;Zhou et al. 2022)在时间序列预测中受到关注。 Transformer 利用自注意力机制来有效捕获数据中的全局依赖性和远程交互。 他们在各种时间序列预测任务中取得了最先进(SOTA)的结果。 与预期相反,最近的研究(Zeng 等人,2023)表明,即使是基本的单变量线性模型,在广泛使用的长期预测基准上也能远远优于复杂的多元 Transformer 模型。 尽管基于 Transformer 的模型取得了重大进步,但这一意外发现凸显了线性模型的有效性。 在本文中,我们引入了用于时间序列预测的 Mixer 架构,以充分利用线性模型的性能,该架构是通过堆叠 MLP 设计的。 并且我们将 Mixer 与 Unet 架构结合起来,整合不同层次的特征来构建更全面、更丰富的表示
Stationarization for Time Series Forecasting
平稳化是时间序列分析的基本假设,使我们能够应用各种模型来有效捕获数据中的模式并增强模型的稳健性。 为了稳定时间序列数据,传统方法采用各种预处理方法(例如差分)来消除数据中的趋势、季节性和非平稳性。 对于深度模型,非平稳性的存在以及随之而来的数据分布变化给时间序列预测带来了重大挑战。 为了解决这个问题,人们通常探索并采用平稳化作为深度模型输入的预处理步骤(Liu et al. 2022b)。 通过将数据转换为更平稳的形式,这些方法旨在减轻与非平稳性相关的困难,并通过深度模型实现更有效的训练和预测。 归一化是一种广泛采用的平稳化方法,旨在通过将数据转换为更符合模型的范围来减轻非平稳特征对学习过程的负面影响。
虽然应用归一化可以解决非平稳性问题,但它引入了潜在的问题(Kim 等人,2021)。 标准化可能会无意中消除非平稳信息,而这些信息可能为预测未来值提供有价值的见解。 因为归一化会改变特征的分布,可能会阻碍模型捕获时间序列的细微动态的能力。 一些研究(Kim et al. 2021;Liu et al. 2022b)显式地将通过输入归一化删除的信息返回给模型,消除了模型重建原始分布的需要,从而降低了建模难度。 然而,直接平稳化时间序列会损害模型对特定时间依赖性进行建模的能力。 因此,我们提出了一种通过约束模型处理前后数据的平稳性差异来进行平稳性校正的方法。 该方法明确地传达了数据分布的统计特征,同时保持了数据中的时间依赖性。
三、Methodology
U-Mixer的架构如图1所示,详细内容将在下面的章节中介绍。
Notations
定义历史数据为
X
∈
R
C
×
L
=
{
x
i
∣
i
∈
[
1
,
L
]
}
X\in\mathbb{R}^{C\times L}=\{x_{i}\mid i\in[1,L]\}
X∈RC×L={xi∣i∈[1,L]}。 这里L表示输入序列的长度,C是通道(或变量)的数量。
x
i
x_i
xi 是时间步 i 处的维度为 C 的向量。 令地面真值未来值为
Y
∈
R
C
×
H
=
{
x
i
∣
i
∈
[
L
+
1
,
L
+
H
]
}
Y\in\mathbb{R}^{C\times H}=\{{x_{i}}\mid i\in[L+1,L+H]\}
Y∈RC×H={xi∣i∈[L+1,L+H]}。 这里H表示预测序列的长度。 我们专注于使用学习模型M来分析X并实现对Y值的预测,该过程可以表示为
Y
^
=
M
(
X
)
\hat{Y} = \mathcal{M}(X)
Y^=M(X)。
Y
^
\hat{Y}
Y^表示预测结果。

图 1:U-Mixer 的架构,由 perpatch 嵌入、Unet 编码器-解码器、平稳性校正和预测头组成。
Normalization and Patch Embedding
输入数据X经过归一化过程,即: X = X − μ i n σ i n X=\frac{X-\mu_{in}}{\sigma_{in}} X=σinX−μin。 这里 μ i n and σ i n \mu_{in}\text{ and }\sigma_{in} μin and σin分别是X中所有通道的均值和方差组成的向量。 通过这个过程,数据变化的范围被调整到更合适的范围,有助于增强模型的稳定性和性能。
归一化后,X 被分为重叠或不重叠的块。 将 patch 长度定义为 P,将两个连续 patch 之间的步长定义为 S。我们可以得到 patch 序列 X p ∈ R ( C × N ) × P X_{p} \in \mathbb{R}^{(C\times N)\times P} Xp∈R(C×N)×P。 这里 N = ⌊ L − P S ⌋ + 2 \lfloor\frac{L-P}{S}\rfloor+{2} ⌊SL−P⌋+2 是补丁的数量。 ⌊·⌋ 为下限函数。 我们重复最后一列 X S 次,并在修补之前将其填充到原始序列。
补丁被映射到嵌入 X d ∈ R ( C × N ) × D X_{d}\in\mathbb{R}^{(C\times N)\times D} Xd∈R(C×N)×D,其中 D 是潜在空间维度。 我们使用线性投影 W v a l ∈ R P × D W_{val}\in\mathbb{R}^{P\times D} Wval∈RP×D 来学习映射关系,并使用加性位置编码 W p o s ∈ R ( C × N ) × D W_{pos}\in\mathbb{R}^{(C\times N)\times D} Wpos∈R(C×N)×D 来提供有关补丁相对位置的信息。 因此, X d = X p W v a l + W p o s X_d = X_pW_{val} + W_{pos} Xd=XpWval+Wpos。 然后 X − d X-d X−d 将被输入 Unet 编码器-解码器以捕获不同补丁和通道之间的依赖关系。 因为模型处理会导致patches中的分布发生变化,这里我们还需要记录 X − d X-d X−d的均值μx、方差σx和自相关矩阵 R ( X d ) R(X_{d}) R(Xd),这样模型输出的分布就会恢复为 随后的平稳性校正操作。
Unet Encoder-decoder
如图2所示,U-Mixer引入了一种新颖的时间序列预测网络,将Unet架构与Mixer架构相结合。

图 2:U-Mixer 的 Unet 编码器-解码器。 编码器和解码器都是 MLP 块。 术语“合并”是指不同级别的特征的组合过程。
U-Mixer采用Unet多级编码器-解码器结构。 编码器采用分层结构,从嵌入 Xd 中逐步提取低层和高层特征。 每个编码器负责将输入嵌入转换为捕获关键特征和上下文信息的高维表示。 将编码器的输入定义为:

X
i
n
,
i
X_{in,i}
Xin,i表示i层编码器的输入,M是层数。 编码器的输出可以表示为:

X
o
u
t
,
i
X_{out,i}
Xout,i 是 i 级编码器的输出,
M
e
n
,
i
\mathcal{M}_{en,i}
Men,i 指 i 级编码器。
解码器还采用分层结构,逐步分析编码器生成的表示。 每个解码器负责通过分析前一个解码器的输出的表示来生成解析的表示。 在解析过程中,每个解码器还需要考虑同一级别编码器的输出,以保留和利用同一级别的特征。 这个过程是通过相应级别的跳跃连接来实现的。 解码器的输入可以形式化为:
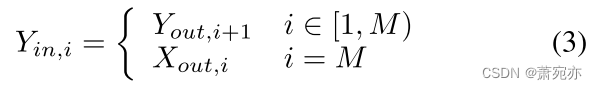
Y
i
n
,
i
Y_{in,i}
Yin,i表示i层解码器的输入。 解码器的输出定义为:

Y
o
u
t
,
i
Y_{out,i}
Yout,i是 i 级解码器的输出,
M
d
e
,
i
\mathcal{M}_{de,i}
Mde,i 指 i 级解码器。 Wy 是一个简单的线性层,用于合并同一级别编码器和前一个解码器生成的特征。
为了便于描述,编码器解码器结构的最终输出被定义为 Y d ∈ R ( C × N ) × D = Y o u t , 1 Y_{d}\in\mathbb{R}^{(C\times N)\times D} = Y_{out,1} Yd∈R(C×N)×D=Yout,1。

图 3:MLP 模块。 (a) 是 MLP 块,包含一个时间 MLP 层和一个通道 MLP 层。 (b)是MLP的具体结构,它由两个全连接层和一个GELU非线性组成。
MLP Block
编码器和解码器都是 MLP 块,如图 3(a) 所示。 MLP块包含两个MLP层,分别用于实现临时交互和通道交互。 首先使用一个 MLP 层在时间维度上对输入数据进行交互,其中包含多个用于独立处理每个通道的 MLP。 该过程在不同通道之间没有交互,以避免由于通道之间的分布差异而影响时间交互。 层归一化后,输出被转置。 另一个MLP层用于在通道维度上进行交互。 层归一化后,输出将转回其之前的形状。 在交互过程中,我们还采用跳跃连接来连接MLP层的输入和输出特征,减少特征变换引入的信息损失,并提供更全面的特征表示。 MLP 由两个线性层、一个 GELU 激活函数和一个 dropout 组成,如图 3(b) 所示。 作为 MLP 的核心组件,线性层对输入进行线性变换以学习特征的线性组合。 GELU 通过对输入应用高斯误差线性变换来实现非线性映射,广泛应用于时间序列预测。 Dropout 通过降低网络对特定特征或输入模式的敏感性来提高模型的鲁棒性。
Stationarity Correction
由于从输入中去除了非平稳信息,数据的分布发生了显着的变化。 现有的恢复数据分布的方法主要关注均值和方差等统计度量,而不考虑数据内的时间依赖性。 因此,原始数据中的趋势和季节性等基本特征可能会受到影响。 因此,我们引入了一种新颖的平稳性校正方法,该方法约束模型处理前后时间序列的平稳性之间的关系,以纠正数据分布,同时保留数据依赖性。
时间序列的平稳性主要体现在均值和协方差两个方面。 均值主要负责从统计角度约束分布,而协方差则从时间依赖性角度约束分布。 数据分布均值的变化通常通过全局加法或减法运算来实现,并且不会影响协方差。 然而,调整协方差可能会导致数据分布均值的变化。 因此,我们首先调整数据的协方差。 协方差 C o v ( X d , X d i ) Cov(X_{d},X_{d}^{i}) Cov(Xd,Xdi)可以表示序列Xd与其第i个滞后序列之间的依赖关系,但不足以完全描述整个时间序列的时间依赖关系。 因此,我们引入自相关矩阵来对时间序列依赖性提供更全面的约束。
定义
R
(
X
d
)
∈
R
L
×
L
=
{
R
i
,
j
(
X
d
)
∣
i
,
j
∈
[
1
,
L
]
}
R(X_{d}) \in \mathbb{R}^{L\times L} = \{R_{i,j}(X_{d}) | i,j \in [1,L]\}
R(Xd)∈RL×L={Ri,j(Xd)∣i,j∈[1,L]}为Xd的自相关矩阵,
R
i
,
j
(
X
d
)
R_{i,j}(X_d)
Ri,j(Xd)=
C
o
v
(
X
d
i
,
X
d
j
)
σ
x
i
σ
x
j
\frac{Cov(X_{d}^{i},X_{d}^{j})}{\sqrt{\sigma_{x}^{i}\sigma_{x}^{j}}}
σxiσxjCov(Xdi,Xdj)。 这里Cov(·)是协方差的计算。
X
d
i
X_d^i
Xdi表示
X
d
X_d
Xd 的第i 个滞后序列,
σ
d
i
\sigma_d^{i}
σdi 表示
X
d
i
X_d^i
Xdi 的方差。 我们使用矩阵α对模型
Y
d
Y_d
Yd的输出进行仿射变换,使得自相关矩阵
R
(
α
Y
d
)
R(\alpha Y_{d})
R(αYd)逼近
R
(
X
d
)
R(X_{d})
R(Xd)。 这里α=
[
α
1
,
α
2
,
⋯
,
α
L
]
∈
R
1
×
L
[\alpha_{1},\alpha_{2},\cdots,\alpha_{L}]\in\mathbb{R}^{1\times L}
[α1,α2,⋯,αL]∈R1×L是矩阵,αi是标量。
R
(
X
d
)
a
n
d
R
(
α
Y
d
)
R(X_{d})\mathrm{~and~}R(\alpha Y_{d})
R(Xd) and R(αYd)之间的约束可以表示为:

Y
d
Y_{d}
Yd 是非平稳时间序列,将
Y
d
Y_{d}
Yd 乘以 α 将导致
Y
d
Y_{d}
Yd 中的数据点之间的变化按系数 α2 缩放。 所以Mα 等价于:

Here:

根据 Wiener-Khinchin 定理 (Cohen 1998),我们可以通过快速傅立叶变换 (FFT) 来加速 αi 的计算:
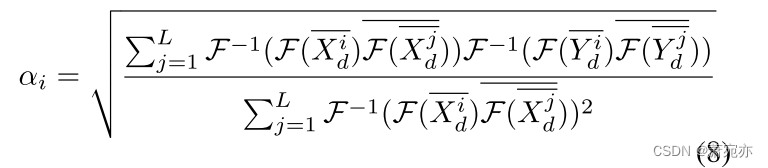
X
d
a
n
d
Y
d
X_{d} \mathrm {and} Y_{d}
XdandYd 的均值必须为零才能满足 Wiener-Khinchin 定理。 这里
X
d
i
‾
=
X
d
i
−
μ
x
i
\overline{X_d^i}=X_d^i-\mu_x^i
Xdi=Xdi−μxi 且
Y
d
i
‾
=
Y
d
i
−
μ
y
i
\overline{Y_d^i}=Y_d^i-\mu_y^i
Ydi=Ydi−μyi。
μ
x
i
a
n
d
μ
y
i
\mu_{x}^{i}\mathrm{~and~}\mu_{y}^{i}
μxi and μyi分别是
X
d
i
a
n
d
Y
d
i
X_d^{{i}}\mathrm{~and~}Y_d^i
Xdi and Ydi 的平均值。 α由
X
d
‾
a
n
d
Y
d
‾
\overline{X_{d}}\mathrm{~and~}\overline{Y_{d}}
Xd and Yd确定。
输出 Y d Y_{d} Yd可以更新为 Y ^ d ∈ R ( C × N ) × D \hat{Y}_{d} \in \mathbb{R}^{(C\times N)\times D} Y^d∈R(C×N)×D= α Y d + ▽ μ , ▽ μ = μ x − μ y \alpha Y_d+\bigtriangledown_\mu,\bigtriangledown_\mu=\mu_x-\mu_y αYd+▽μ,▽μ=μx−μy 用于调整 Y d a n d X d Y_{d}\mathrm{~and~}X_{d} Yd and Xd 之间的均值差。 层范数 层范数 线性 GELU 线性

表 1:在长期预测中,U-Mixer 与大规模现实世界时间序列数据集上的 SOTA 基准进行比较。
Instance Normalization and Learning Objective
我们通过线性层将
Y
^
d
\hat{Y}_{d}
Y^d 展平为
Y
p
^
∈
R
C
×
(
L
+
H
)
\hat{Y_p}\in\mathbb{R}^{C\times(L+H)}
Yp^∈RC×(L+H)。 然后我们使用实例归一化来减轻输入 X 和预测结果之间的分布偏移效应。 因此 U-Mixer 的输出为
Y
^
∈
R
C
×
H
=
Y
^
p
[
:
,
τ
]
×
σ
i
n
+
μ
i
n
\hat{Y}\in\mathbb{R}^{C\times H}=\hat{Y}_{p}[:,\tau]\times\sigma_{in}+\mu_{in}
Y^∈RC×H=Y^p[:,τ]×σin+μin,
τ
=
L
:
L
+
H
\tau = L : L+H
τ=L:L+H。我们选择 L1 损失函数来衡量预测与真实值之间的差异, 并且损失从整个模型的输出传播回来。 与时间序列预测任务中常用的MSE损失函数相比,L1损失函数对异常值的敏感度较低,这使得模型能够获得更稳健的性能。 我们模型的损失是:
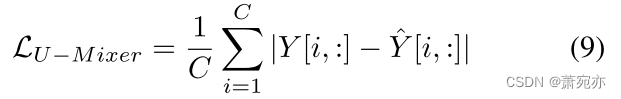
四、Experiments
Datasets
我们主要在长期预测中的六个大型现实世界时间序列数据集上评估 U-Mixer。 (1)电力变压器温度(ETT)(Wu et al. 2021)数据包含从电力变压器收集的电力负载特征和油温,由七个特征组成。 遵循与 Informer 相同的协议(Zhou et al. 2021),我们将数据分为四个数据集:ETTh1、ETTh2、ETTm1 和 ETTm2。 (2)电力消耗负载(ECL)(Wu et al. 2021)数据包含 2012 年至 2014 年 321 个客户的每小时用电量。(3)交通(He et al. 2022)数据是来自加利福尼亚州的每小时数据的集合 交通部描述了旧金山思科高速公路上不同传感器测量的不同车道的占用率。 (4)汇率(Lai et al. 2018)数据收集1990年至2016年8个国家每日汇率的面板数据。(5)天气(Nie et al. 2023)数据记录每10分钟收集一次的21个气象指标 来自马克斯·普朗克生物地球化学研究所气象站2020年的数据。 (6) M4 (Wu et al. 2023)是短期预报数据集,包含6个子集:M4-Yearly、M4-Quarterly、M4-Monthly 、M4-弱、M4-每日和 M4-每小时。 我们按照时间顺序将所有数据集分为训练集、验证集和测试集,ETT 数据集的比例为 6:2:2,其他数据集的比例为 7:1:2。
 表 2:U-Mixer 与 M4 数据集上的 SOTA 基准在短期预测方面的比较。
表 2:U-Mixer 与 M4 数据集上的 SOTA 基准在短期预测方面的比较。
Model Configuration and Metrics
U-Mixer 通过 Pytorch 实现,并在 Nvidia A40 GPU (48GB) 上进行训练。 长期预测默认使用以下模型配置:输入序列长度 L = 96,补丁长度 P = 16,步长 S = 8,预测序列长度 H ∈ {96, 192, 336, 720},补丁数量 级别 M = 3,批量大小设置为 16。对于短期预测,模型配置为:补丁长度 P = 8,步长 S = 4,批量大小设置为 32。模型训练运行 10 个 epoch,并且 优化由 Adam 执行。 为了提高实施结果的可重复性,我们修复了随机种子。 我们采用均方误差 (MSE) 和平均绝对误差 (MAE) 进行长期预测评估。 继 N-BEATS(Oreshkin 等人,2019)之后,我们还采用对称平均绝对百分比误差(SMAPE)、平均绝对比例误差(MASE)和总体加权平均值(OWA)进行短期预测。
SOTA Benchmarks
我们将 U-Mixer 与来自五个不同类别的以下 16 种 SOTA 方法进行比较:(1)基于 RNN 的模型:LSTM(Hochreiter 和 Schmidhuber 1997)和 LSSL(Gu、Goel 和 R´e 2022)。 (2) 基于 MLP 的模型:LightTS (Zhang et al. 2022) 和 DLinear (Zeng et al. 2023)。 (3) 基于 CNN 的模型:TCN (Bai, Kolter, and Koltun 2018) 和 TimesNet (Wu et al. 2023)。 (4) 基于 Transformer 的模型:LogTrans (Li et al. 2019)、Reformer (Kitaev, Kaiser, and Levskaya 2020)、Informer (Zhou et al. 2021)、Pyraformer (Liu et al. 2021)、Autoformer (Wu et al. 2021) al. 2021)、FEDformer (Zhou et al. 2022)、非稳态变压器 (Liu et al. 2022b) 和 ETSformer (Woo et al. 2022)。 (5) 基于分解的模型:N-BEATS (Oreshkin et al. 2019) 和 N-HiTS (Challu et al. 2023)。

表 3:ETTh2、Weather 和 M4 数据集的消融研究结果。
Overall Comparison
表 1 显示了 MSE 和 MAE 测量的长期预测性能,表 2 显示了 SMAPE、MASE 和 OWA 测量的短期预测性能。 我们可以观察到U-Mixer很好地平衡了短期和长期预测,并取得了最好的短期和长期预测性能。 在对 8 个数据集进行的 64 次长期预测中,我们在 56 个案例中取得了最佳结果,并将 MSE/MAE 与现有最佳结果相比提高了 14.5%/7.7%。 对于 M4 数据集的短期预测,我们几乎实现了所有最优结果。 特别是,我们发现基于 RNN 的方法表现出明显较差的性能。 对于长期预测,基于 MLP、基于 CNN 和基于 Transformer 的方法之间没有显着差异。 除了我们的模型之外,基于分解的方法在短期预测方面也表现出领先地位。
Ablation Study
为了更好地评估 Unet 编码器-解码器(UE)和平稳性校正(SC),我们进行了考虑消融的补充实验。 这里 w/o UE 和 w/o SC 是 U-Mixer 的变体。 在 w/o UE 中,我们设置 Unet 编码器-解码器级别 M = 0。在 w/o SC 中,我们删除 Yearly Quart。 其他平均 平稳性校正过程。 我们将批量大小设置为 16,输入序列长度设置为 96,水平线设置为 {96,192,336,720},并在所有消融实验中使用相同的参数设置。 平均结果如表 3 所示。w/o UE 和 w/o SC 的所有指标都明显比 U-Mixer 差。 完整的U-Mixer可以获得最好的效果,证明去掉其中的任何组件都会影响效果。 Unet编解码器和平稳性校正是必要且有效的。

图 4:U-Mixer 对多个数据集的预测结果可视化。
Showcases
为了进一步展示 U-Mixer 的预测性能,我们在 ETTh1、电力、ETTh2 和流量数据集上可视化结果。 如图 4 所示,ETTh2 和 Traffic 数据集表现出更清晰的周期性模式,我们的方法可以有效地预测地面实况。 由此可见U-Mixer在捕捉周期方面的强大能力。 相比之下,ETTh1 和 Electricity 的模式相对不太明显。 我们的方法设法在合理的范围内捕获它们的周期性,并对它们的趋势做出一定的预测。 验证了U-Mixer性能在各种数据特征下的鲁棒性。
Parameter Sensitivity
我们选择通过改变级别M的数量和补丁长度P来对ETTm2和Exchange数据集进行U-Mixer的敏感性分析。如图5所示,可以得出结论,我们的模型对参数M不高度敏感。 总体而言,当M设置为3时,可以获得最佳结果。此外,随着M的增加,模型的训练时间也会增加。 因此,我们选择 M = 3 作为模型的参数。 对于参数 P,我们可以看出我们的模型在 ETTm2 数据集上对参数 P 表现出较高的敏感度,而在 Exchange 数据集上的敏感度较低。 P的值也会影响训练时间。 当P设置为8或16时,训练时间相对较短,P=16的结果优于P=8。因此,我们将P=16设置为指定值。

五、Conclusion
在本文中,我们研究了时间序列预测任务中的非平稳性挑战,并提出了一种新颖的预测模型 U-Mixer。 我们结合Unet和Mixer架构来捕获不同级别的补丁和通道之间的局部依赖关系,以获得时间序列的综合表示。 更重要的是,我们提出了一种平稳性校正方法来处理非平稳性引起的分布偏移,同时保留时间依赖性。 我们的模型在六个真实数据集上展示了最先进的短期和长期预测性能,各种实验的整体优越性进一步验证了其有效性和鲁棒性。























 1883
1883

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








