TIMEMIXER: DECOMPOSABLE MULTISCALE MIXING FOR TIME SERIES FORECASTING

萧宛亦

已于 2024-04-25 16:25:19 修改

阅读量1.8k

点赞数 3

文章标签：人工智能

于 2024-04-20 19:20:01 首次发布

原文链接：https://arxiv.org/abs/2310.11959

版权

本文提出TimeMixer模型解决时间序列预测难题。它采用多尺度混合架构，含过去可分解混合和未来多预测混合模块，能利用多尺度序列解耦变化与互补预测能力。实验表明，该模型在长短期预测任务中达先进水平，且运行效率良好。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

系列文章目录

TIMEMIXER：用于时间序列预测的可分解多尺度混合 ICLR 2024

摘要

时间序列预测广泛应用于交通规划和天气预报等广泛应用中。然而，现实世界的时间序列通常呈现复杂的时间变化，使得预测极具挑战性。超越简单分解和多周期分析的主流范式，我们以多尺度混合的新颖观点分析时间变化，该观点基于直观但重要的观察，即时间序列在不同采样尺度下呈现不同的模式。微观和宏观信息分别反映在精细和粗尺度上，从而可以从本质上理清复杂的变化。基于这一观察，我们提出 TimeMixer 作为完全基于 MLP 的架构，具有过去可分解混合 (PDM) 和未来多重预测混合 (FMM) 模块，以在过去的提取和未来的预测阶段充分利用解开的多尺度序列。具体来说，PDM将分解应用于多尺度序列，进一步将分解后的季节成分和趋势成分分别在由细到粗和由粗到细的方向上混合，依次聚合微观季节和宏观趋势信息。 FMM 进一步集成了多个预测变量，以在多尺度观测中利用互补的预测功能。因此，TimeMixer 能够在长期和短期预测任务中实现一致的最先进性能，并具有良好的运行时效率。

一、介绍

时间序列预测在广泛的应用中受到了极大的兴趣，例如经济学（Granger & Newbold，2014）、能源（Martín et al.，2010；Qian et al.，2019）、交通规划（Chen et al.，2001） ; Yin et al., 2021）和天气预报（Wu et al., 2023b），即根据过去的时间序列观测来预测未来的时间变化（Wu et al., 2023a）。然而，由于现实世界或系统的复杂性和非平稳性，观测到的序列通常呈现出错综复杂的时间模式，其中增加、减少、波动等多种变化深度混合，给观测序列带来了严峻的挑战。预测任务。

最近，深度模型在时间序列预测方面取得了可喜的进展。代表性模型通过精心设计的架构捕获时间变化，这些架构跨越了广泛的基础主干，包括 CNN（Wang 等人，2023；Wu 等人，2023a；Hewage 等人，2020）、RNN（Lai 等人）等人，2018；Salinas 等人，2020），Transformer（Vaswani 等人，2017；Zhou 等人，2021；Wu 等人，2021；Zhou 等人，2022b； Nie 等人，2023）和 MLP（Zeng 等人，2023；Zhang 等人，2022；Oreshkin 等人，2019；Challu 等人，2023）。在精细模型架构的开发中，为了解决复杂的时间模式，这些深层模型还涉及一些特殊的设计。广泛认可的范式主要包括级数分解和多周期分析。作为一种经典的时间序列分析技术，分解作为基本模块被引入到深度模型中（Wu et al., 2021），将复杂的时间模式分解为更可预测的成分，例如季节性和趋势，从而有利于预测过程（Zeng 等，2023；Zhou 等，2022b；Wang 等，2023）。此外，时间序列预测还涉及多周期分析（Wu et al., 2023a; Zhou et al., 2022a），将混合时间变化分解为具有不同周期长度的多个分量。借助这些设计，深度模型能够从混乱的变化中突出时间序列的固有属性，并进一步提高预测性能。

除了上述设计之外，我们进一步观察到时间序列在不同采样尺度下呈现出明显的时间变化，例如，每小时记录的交通流量呈现一天中不同时间的交通变化，而对于每日采样的序列，这些细粒度的交通流量呈现出一天中不同时间的交通变化。变化消失，但与假期相关的波动出现。另一方面，宏观经济的走势主导着年平均格局。这些观察自然需要多尺度分析范式来理清复杂的时间变化，其中精细和粗尺度可以分别反映微观和宏观信息。特别是对于时间序列预测任务，还值得注意的是，未来的变化是由多个尺度的变化共同决定的。因此，在本文中，我们尝试从多尺度混合的新颖视角来设计预测模型，该模型能够同时利用多尺度序列的解耦变化和互补预测能力。

从技术上讲，我们提出了具有多尺度混合架构的 TimeMixer，该架构能够通过过去可分解混合 (PDM) 块从过去的变化中提取基本信息，然后通过未来多重预测器混合 (FMM) 块预测未来序列。具体来说，TimeMixer 首先通过平均下采样生成多尺度观测值。其次，PDM采用可分解的设计，通过将分解后的多尺度季节性和趋势分量分别在细到粗和粗到细方向上混合，更好地应对季节和趋势变化的不同属性。凭借我们新颖的设计，PDM 能够成功聚合从最精细的系列开始的详细季节性信息，并深入研究宏观趋势成分以及较粗尺度的知识。在预测阶段，FMM 集成了多个预测变量，以利用多尺度观测的互补预测功能。凭借我们细致的架构，TimeMixer 在长期和短期预测任务中实现了一致的最先进性能，在我们所有的实验中都具有卓越的效率，涵盖了广泛的成熟基准。我们的贡献总结如下：

• 超越以前的方法，我们从多尺度混合的新颖视角解决序列预测中复杂的时间变化，同时利用多尺度序列的解开变化和互补预测能力。
• 我们提出TimeMixer 作为一种简单但有效的预测模型，在我们定制的可分解和多预测器混合技术的支持下，它能够在历史提取和未来预测阶段结合多尺度信息。
• TimeMixer 在长期和短期预测任务中均实现了一致的最先进性能，并在各种基准测试中具有卓越的效率。

二、相关工作

2.1 深度时间序列预测中的时间建模

作为时间序列分析的关键问题（Wu et al., 2023a），时间建模已被广泛探索。根据基础主干，深度模型可以大致分为以下四种范式：基于 RNN、CNN、Transformer 和 MLP 的方法。通常，基于 CNN 的模型沿时间维度采用卷积核来捕获时间模式（Wang 等人，2023；Hewage 等人，2020）。基于 RNN 的方法采用循环结构来建模时间状态转换（Lai et al., 2018；Zhao et al., 2017）。然而，基于 RNN 和 CNN 的方法都存在感受野有限的问题，限制了长期预测能力。近年来，受益于全局建模能力，基于 Transformer 的模型在长期序列预测中得到了广泛认可（Zhou et al., 2021; Wu et al., 2021; Liu et al., 2022b; Kitaev et al., 2021）。，2020；Nie et al.，2023），它可以通过注意力机制自适应地捕获长期时间依赖性。此外，多层投影（MLP）也被引入到时间序列预测中（Oreshkin et al., 2019; Challu et al., 2023; Zeng et al., 2023），在预测性能和效率上都取得了良好的表现。

此外，还提出了几种具体的设计，以更好地捕获复杂的时间模式，包括序列分解和多周期性分析。首先，对于序列分解，Autoformer（Wu et al., 2021）提出了基于移动平均的序列分解块，将复杂的时间变化分解为季节和趋势分量。随后，FEDformer（Zhou et al., 2022b）通过多核移动平均增强了级数分解块。 DLinear（Zeng et al., 2023）利用级数分解作为线性回归之前的预处理。 MICN（Wang et al., 2023）还将输入序列分解为季节性和趋势项，然后整合全球和本地背景进行预测。对于多周期性分析，N-BEATS (Oreshkin et al., 2019) 用多个三角基函数拟合时间序列。 FiLM（Zhou et al., 2022a）将时间序列投影到勒让德多项式空间中，其中不同的基函数对应于原始序列中的不同周期分量。最近，TimesNet（Wu et al., 2023a）采用傅立叶变换将时间序列映射为具有不同周期长度的多个分量，并提出了一种模块化架构来处理分解的分量。

与上述设计不同，本文探讨了时间序列预测中的多尺度混合架构。尽管存在一些具有时间多尺度设计的模型，例如具有金字塔注意力的 Pyraformer (Liu et al., 2021) 和具有分叉下采样树的 SCINet (Liu et al., 2022a)，但它们的未来预测并未利用这些信息同时从过去的观察中提取不同尺度的数据。在 TimeMixer 中，我们提出了一种新的多尺度混合架构，其中包含 Past-Decomposable-Mishing，以利用解开的序列进行多尺度表示学习，并利用 Future-Multipredictor-Mishing 来集成多尺度序列的互补预测技能，以实现更好的预测。

2.2 混合网络

混合是一种有效的信息整合方式，已应用于计算机视觉和自然语言处理。例如，MLP-Mixer（Tolstikhin et al., 2021）设计了一种用于图像识别的两级混合结构，它将通道信息和补丁信息依次与线性层混合。 FNet（Lee-Thorp et al., 2022）用简单的傅立叶变换替换了 Transformer 中的注意力层，实现了句子的高效标记混合。在本文中，我们进一步探讨了时间序列预测中的混合结构。与之前的设计不同，TimeMixer 提出了可分解的多尺度混合架构，并区分了过去信息提取和未来预测阶段的混合方法。

三、时间混合器

给定一个具有一个或多个观测变量的序列 x，时间序列预测的主要目标是利用过去的观测值（长度-P）来获得最可能的未来预测（长度-F）。如上所述，准确预测的关键挑战是解决复杂的时间变化。在本文中，我们提出了多尺度混合的 TimeMixer，受益于多尺度序列的解开变化和互补预测能力。从技术上讲，TimeMixer 由多尺度混合架构组成，其中过去可分解混合和未来多重预测器混合分别用于过去信息提取和未来预测。

3.1 多尺度混合架构

不同尺度的时间序列自然表现出不同的属性，其中精细尺度主要描绘细节模式，而粗尺度则突出宏观变化（Mozer，1991）。这种多尺度视图可以本质上理清多个成分中的复杂变化，从而有利于时间变化建模。还值得注意的是，特别是对于预测任务，多尺度时间序列由于其独特的主导时间模式而呈现出不同的预测能力（Ferreira et al., 2006）。因此，我们在多尺度混合架构中提出了 TimeMixer，以利用具有针对过去提取和未来预测阶段的独特设计的多尺度系列。

如图1所示，为了解开复杂变化，我们首先将过去的观测值 $\mathrm{x~}\in\mathbb{R}^{P\times C}$ 平均池化到M个尺度，最终得到一组多尺度时间序列 $\mathcal X=\{\mathbf{x}_{0},\cdots,\mathbf{x}_{M}\}$ ，其中 $\mathbf{x}_{m}\in\mathbb{R}^{\lfloor\frac{P}{2^{m}}\rfloor\times C},m\in\{0,\cdots,M\}$ ， C为变量数。最低层次的序列 $\mathbf{x}_0=\mathbf{x}$ 是输入序列，它包含了最细微的时间变化，而最高层次的序列 $\mathbf{x}_{M}$ 是宏观变化。然后通过嵌入层将这些多尺度序列投影为深度特征 $X^{0}$ ，可以形式化为 $\mathcal{X}^0=\mathrm{Embed}(\mathcal{X})$ 。通过上述设计，我们得到了输入序列的多尺度表示。

在这里插入图片描述
图1:TimeMixer的整体架构，由过去可分解混合和未来多预测混合组成，分别用于过去观察和未来预测。

接下来，我们利用堆叠的过去-分解-混合(PDM)块来混合不同尺度的过去信息。对于第l层，输入为 $X^{l-1}$ ,PDM的过程可以形式化为:

在这里插入图片描述
式中，L为总层， $\chi^l=\{\mathbf{x}_0^l,\cdots,\mathbf{x}_M^l\},\mathbf{x}_m^l\in\mathbb{R}^{\lfloor\frac{P}{2^m}\rfloor\times d_{\mathrm{model}}}$ 表示具有dmodel通道的混合过去表示。下一节将描述PDM的更多细节。

对于未来预测阶段，我们采用future - multipredictor - mixing (FMM)块对提取的多尺度过去信息 $X^{L}$ 进行集合，生成未来预测，即:

在这里插入图片描述

$\widehat{\mathbf{x}}\in\mathbb{R}^{F\times C}$ 表示这是最后的预测。通过上述设计，TimeMixer可以成功地从解耦的多尺度观测中捕获重要的过去信息，并利用多尺度过去信息预测未来。

3.2过去的可分解混合

我们观察到，对于过去的观测，由于现实世界序列的复杂性，即使是最粗糙的尺度序列也呈现混合变化。如图1所示，顶层的序列仍然同时呈现出明显的季节性和趋势。值得注意的是，季节和趋势分量在时间序列分析中具有不同的特性(Cleveland et al.， 1990)，分别对应于短期和长期变化或平稳和非平稳动态。因此，我们提出了过去分解混合(past - decomposition - mixing, PDM)块，将分解后的季节分量和趋势分量在多个尺度上分别混合，而不是直接混合整个多尺度序列。

具体而言，对于第l个PDM块，我们首先通过Autoformer (Wu et al.， 2021)的级数分解块将多尺度时间序列 $X_{l}$ 分解为季节部分 $S^{l}=\{\mathbf{s}_{0}^{l},\cdots,\mathbf{s}_{M}^{l}\}$ 和趋势部分 $\mathcal{T}^l=\{\mathbf{t}_0^l,\cdots,\mathbf{t}_M^l\}$ 。如前所述，考虑到季节趋势部分的不同性质，我们分别对季节和趋势项进行混合操作，以实现多尺度信息的交互。总的来说，第l个PDM块可以形式化为:
在这里插入图片描述
其中前馈(·)包含两个线性层，中间有GELU激活函数用于渠道间的信息交互，S-Mix(·)、T-Mix(·)表示季节和趋势混合。

季节混合 在季节性分析中(Box & Jenkins, 1970)，大周期可以看作是小周期的集合，例如由7个日变化形成的交通流量周周期，解决了详细信息在预测未来季节变化中的重要性。

因此，在季节混合中，我们采用自下而上的方法，从较低层次的细尺度时间序列向上吸收信息，可以为较粗尺度的季节性建模补充详细信息。技术上，对于多尺度季节部件集 $S^{l}=\{\mathbf{s}_{0}^{l},\cdots,\mathbf{s}_{M}^{l}\}$ ，我们采用残差方式对第M尺度进行自下而上的混合层，实现自下而上的季节信息交互，其形式为:

在这里插入图片描述

图2:季节混合(a)、趋势混合(b)和未来预测©中的时间线性层。

在这里插入图片描述

其中自下而上混合(·)被实例化为沿时间维具有中间GELU激活函数的两个线性层，其输入维数为 $\left\lfloor\frac P{2^{m-1}}\right\rfloor$ ，输出维数为 $\left\lfloor\frac P{2^{m}}\right\rfloor$ 。请参见图2直观地理解。

趋势混合 与季节部分相反，对于趋势项，详细的变化会在捕捉宏观趋势时引入噪声。请注意，较上层的粗尺度时间序列比下层的时间序列更容易提供清晰的宏观信息。因此，我们采用自顶向下的混合方法，利用粗尺度的宏观知识来指导细尺度的趋势建模。

技术上，对于多尺度趋势分量 $\mathcal{T}^l=\{\mathbf{t}_0^l,\cdots,\mathbf{t}_M^l\}$ ，我们采用残差方式对第M尺度采用top-down - mix层，实现自顶向下的趋势信息交互:

在这里插入图片描述

其中Top-Down-Mixing(·)为两个线性层，中间有一个GELU激活函数，其输入维数为 $\left\lfloor\frac P{2^{m+1}}\right\rfloor$ ，输出维数为 $\left\lfloor\frac P{2^{m}}\right\rfloor$ ，如图2所示。

PDM以季节和趋势混合为基础，将详细的季节信息由细到粗逐步聚合，再从更粗的尺度上利用先验知识深入到宏观趋势信息，最终实现过去信息提取中的多尺度混合。

3.3未来多预测器混合

经过L个PDM块后，我们得到多尺度过去信息为 $\mathcal{X}^L=\{\mathbf{x}_0^L,\cdots,\mathbf{x}_M^L\},\mathbf{x}_m^L\in\mathbb{R}^{\lfloor\frac P{2^m}\rfloor\times d_{\mathrm{model}}}$ 。由于不同尺度的序列表现出不同的主导变化，它们的预测能力也不同。为了充分利用多尺度信息，我们建议将多尺度序列的预测汇总，并将Future-Multipredictor-Mixing块表示为:

在这里插入图片描述

其中， $\widehat{\mathbf{x}}_m\in\mathbb{R}^{F\times C}$ 表示第m个尺度序列对未来的预测，最终输出为 $\widehat{\mathbf{x}}\in\mathbb{R}^{F\times C}.$ 。Predictorm(·)表示第m个尺度序列的预测器，它首先采用单线性层直接从提取的过去信息(图2)中提取长度- $\left\lfloor\frac{P}{2^{m}}\right\rfloor$ 回归到长度- f未来(length- f future)，然后将深度表示投影到C个变量中。注意，FMM是多个预测因子的集合，其中不同的预测因子基于不同尺度的过去信息，使FMM能够整合混合多尺度序列的互补预测能力。

四、实验

我们进行了大量的实验来评估TimeMixer的性能和效率，包括长期和短期预测，包括18个真实世界的基准和15个基线。详细的模型和实验配置见附录A。

表1:基准测试摘要。可预测性等于1减去傅里叶域的熵。
在这里插入图片描述
Benchmarks 对于长期预测，我们在8个成熟的基准上进行了实验:ETT数据集(包括4个子集:ETTh1、ETTh2、ETTm1、ETTm2)、天气、太阳能、电力和交通跟踪(Zhou et al.， 2021;Wu et al.， 2021;Liu et al.， 2022a)。对于短期预测，我们采用了PeMS (Chen et al.， 2001)，其中包含四个公共交通网络数据集(PEMS03, PEMS04, PEMS07, PEMS08)和M4数据集，其中包括10万个不同频率收集的不同时间序列。此外，我们测量了所有数据集的可预测性(Goerg, 2013)。我们观察到ETT、M4和Solar-Energy表现出相对较低的可预测性，这表明在这些基准中存在挑战。表1总结了更多信息。

Baselines我们将TimeMixer与15个基线进行比较，这些基线包括最先进的长期预测模型PatchTST(2023)和先进的短期预测模型TimesNet (2023a)和SCINet (2022a)，以及其他竞争模型，包括Crossformer(2023)、MICN(2023)、FiLM (2022a)、DLinear(2023)、LightTS(2022)、FEDformer (2022b)、Stationary (2022b)， Pyraformer (2021)， Autoformer (2021)， Informer (2021)， N-HiTS(2023)和N-BEATS(2019)。

Unified experiment settings注意，由于输入长度和超参数搜索策略的选择不同，上述基线报告的实验结果不能直接进行比较。为了公平起见，我们尽力提供两种类型的实验。在正文中，我们将所有基线的输入长度对齐，并报告三次重复的平均结果(见附录C的误差条)。在附录中，为了比较模型的上界，我们也进行了全面的超参数搜索，并在附录的表14中报告了最佳结果。

实现细节所有实验都在PyTorch (Paszke等人，2019)中实现，并在单个NVIDIA A100 80GB GPU上进行。我们利用L2损失进行模型训练。根据时间序列长度设置尺度的数量M，以权衡性能和效率。

4.1 MAIN RESULTS

长期预测 如表2所示，TimeMixer在所有基准测试中都实现了一致的最先进性能，涵盖了具有不同频率、变量数和实际场景的各种系列。特别是，TimeMixer以相当大的优势优于PatchTST，天气的MSE降低了9.4%，太阳能的MSE降低了24.7%。值得注意的是，即使在Solar-Energy和ETT等可预测性较低的数据集上，TimeMixer也表现出了良好的性能，进一步证明了TimeMixer的通用性和有效性。

表2:长期预测结果。所有结果均取4个不同预测长度的平均值，即{96,192,336,720}。MSE或MAE越低，表示预测越好。我们将所有实验的输入长度固定为96。完整结果见附录表13。在这里插入图片描述
表3:多变量PEMS数据集的短期预测结果。所有输入长度为96，预测长度为12。MAE、MAPE或RMSE越低，表明预测越好。

表4:单变量M4数据集中的短期预测结果。所有的预测长度都在[6,48]内。较低的SMAPE、MASE或OWA表示较好的预测。;在变压器中表示前器的名称。静止是指非静止变压器。在这里插入图片描述 N-BEATS(2019)的原始论文采用了一种特殊的集成方法来促进性能。为了公平比较，我们去掉集合，只比较纯预测模型。

短期预测 在多变量和单变量设置下，TimeMixer在短期预测方面也表现出色(表3-4)。对于记录城市交通网络的多个时间序列的PeMS基准，由于多变量之间复杂的时空相关性，许多高级模型在该任务中退化很大，如PatchTST(2023)和DLinear(2023)，它们采用了通道无关设计。相比之下，TimeMixer在这一具有挑战性的问题中仍然表现良好，验证了其在处理复杂多元时间序列预测方面的有效性。单变量预测的M4数据集在每小时、每天、每周、每月、每季度和每年不同采样频率下存在不同的时间变化，在不同频率下表现出较低的可预测性和显著的特征。值得注意的是，Timemixer始终在所有频率上表现最佳，这肯定了多尺度混合架构在模拟复杂时间变化方面的能力。

4.2模型分析

消融为了验证timemixer每个组件的有效性，我们在所有18个实验基准上对过去分解混合和未来多预测混合块的每种可能设计进行了详细的烧蚀研究。从表5中，我们有以下观察结果。

排除消融中未来-多预测因子混合②导致模型的短期和长期预测精度显著降低。这表明混合多尺度序列的未来预测可以有效地提高模型的性能。

表5:在M4、PEMS04和ETTm1的predict-336设置中，PDM(分解、季节混合、趋势混合)和FMM块的消融情况。↙表示自下而上的混合，而↙表示自上而下的混合。检查标记“✓”和错误标记“x”分别表示有和没有某些部件。①为TimeMixer的官方设计(完整烧蚀结果见附录F)。
在这里插入图片描述

排除消融中未来-多预测因子混合②导致模型的短期和长期预测精度显著降低。这表明混合多尺度序列的未来预测可以有效地提高模型的性能。对于过去的混合，我们通过逐步去除或更换成分来验证其有效性。在去除季节混合和趋势混合的烧蚀中③和④也会导致性能下降。这说明，仅仅依靠季节或趋势信息的相互作用是不够准确的预测。此外，在烧蚀⑤和⑥中，我们对季节和趋势采用了相同的混合方法。然而，它并不能带来更好的预测性能。类似的情况也发生在⑦采用与我们设计相反的混合策略。这些结果证明了我们的设计在自下而上的季节混合和自上而下的趋势混合中的有效性。同时，在消融⑧和⑨中，我们选择消除分解架构，直接混合多尺度序列。但是，如果没有分解，自下而上和自上而下的混合方法都无法获得良好的性能，这说明了季节趋势分离混合的必要性。此外，在烧蚀过程中，消除整个过去分解混合块会导致模型的预测性能严重下降。上述研究结果突出了适当的过去混合方法对模型最终性能的实质性影响。TimeMixer从对时间序列的认识出发，提出了过去信息提取中最好的混合方法。

季节性和趋势混合可视化 为了直观地理解PDM，我们在图3(a) ~ (b)中可视化了季节性混合和趋势混合的时间线性权重。我们发现季节和趋势项呈现出明显的混合特性，其中季节混合层呈现周期性变化((a)中重复的蓝线)，趋势混合层以局部聚集为主((b)中占主导地位的对角线黄线)。这也验证了对季节项和趋势项采用单独混合技术的必要性。此外，图3©显示了细尺度(尺度0)和粗尺度(尺度3)对季节和趋势项的预测。我们可以观察到，精细尺度的季节项和粗尺度的趋势部分对准确预测至关重要。这一观察结果为我们的设计提供了对季节项使用自下而上混合和趋势组件使用自上而下混合的见解。

在这里插入图片描述
图3:季节混合(Eq. 4)、趋势混合(Eq. 5)和多尺度季节趋势项目预测中的时间线性权重的可视化。所有实验均在输入-96-预测-96设置下的ETTh1数据集上进行。

在这里插入图片描述
图4:在ETTh1数据集的input-96-predict-96设置上，来自不同尺度(Eq. 6中的bxL m)的预测的可视化。实现细节包含在附录A中。

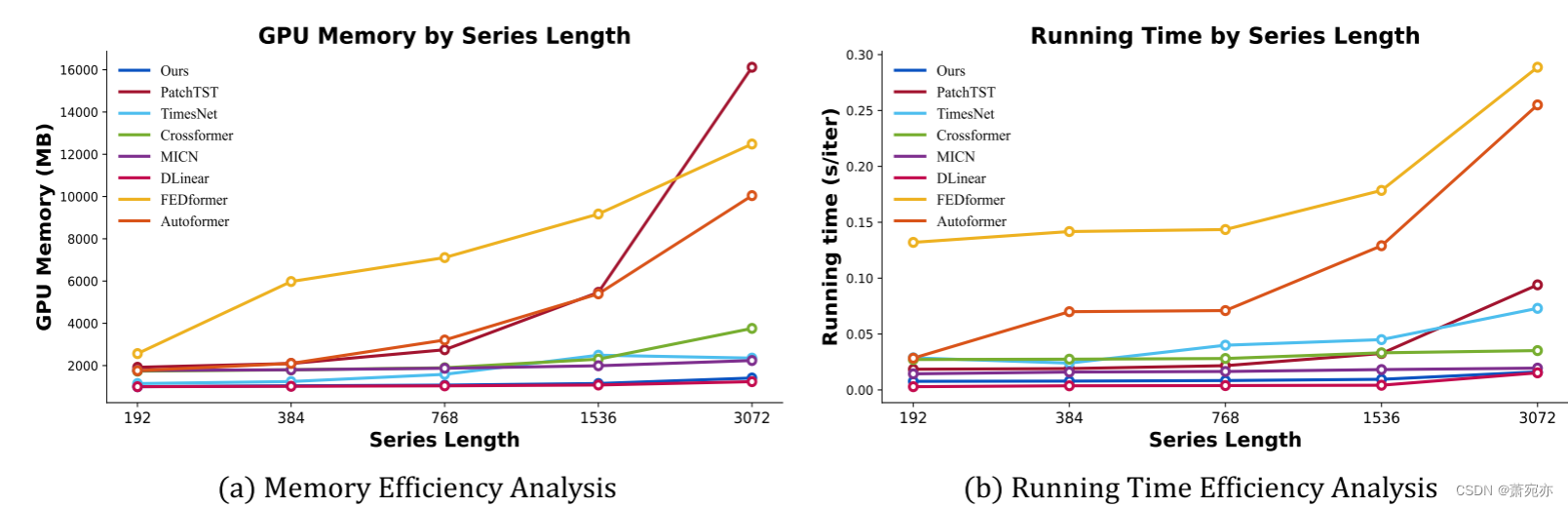
在这里插入图片描述
图5:GPU内存和运行时间的效率分析。结果记录在批量大小为16的ETTh1数据集上。运行时间是102次迭代的平均值。

多预测器可视化为了直观地了解多尺度序列的预测技巧，我们绘制了不同尺度的预测结果图，进行定性比较。图4(a)给出了我们的模型使用future - multipredictor - mixing的总体预测，这表明使用混合尺度对未来的变化进行了准确的预测。为了研究每个单独尺度的组成部分，我们在图4(b) ~ (e)中展示了每个尺度的预测结果。具体而言，精细尺度时间序列的预测结果更集中于时间序列的详细变化，并以更高的精度捕获季节模式。相反，如图4© ~ (e)所示，通过多次降采样，粗尺度序列的预测更多地关注宏观趋势。上述结果还突出了Future-Multipredictor-Mixing在利用多尺度序列的互补预测技能方面的好处。

效率分析我们将运行内存和时间与图5中最先进的模型进行比较，在训练阶段，TimeMixer在GPU内存和运行时间方面始终表现出良好的效率，适用于各种系列长度(从192到3072)。除了长期和短期预测任务的一贯的最先进的表现。

尺度数分析我们从图6中的尺度数(M)来探讨不同序列长度下的影响。具体来说，当m增加时，对于较短的预测长度，性能增益下降。相反，对于较长的预测长度，性能随着M的增加而提高。因此，我们将M设置为长期预测为3，短期预测为1，以权衡性能和效率。

在这里插入图片描述

五、结论

我们提出了具有多尺度混合架构的TimeMixer，以解决时间序列预测中复杂的时间变化问题。通过过去可分解混合和未来多预测混合模块，TimeMixer利用了分离的变化和互补的预测能力。在我们所有的实验中，TimeMixer在长期和短期预测任务中都取得了一致的最先进的性能。此外，得益于完全基于mlp的体系结构，TimeMixer展示了良好的运行时效率。详细的可视化和消融包括为我们的设计提供见解。

我们在附录A中涉及实现细节，包括数据集描述，度量计算和实验配置。源代码以补充材料的形式提供，并在GitHub (https://github.com/kwuking/TimeMixer)中公开，以便再现。

二、使用步骤

1.引入库

代码如下（示例）：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
import  ssl
ssl._create_default_https_context = ssl._create_unverified_context

2.读入数据

代码如下（示例）：

data = pd.read_csv(
    'https://labfile.oss.aliyuncs.com/courses/1283/adult.data.csv')
print(data.head())

该处使用的url网络请求的数据。

总结

提示：这里对文章进行总结：

例如：以上就是今天要讲的内容，本文仅仅简单介绍了pandas的使用，而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。